Another method of combining functions is by composition, where a function contains another function. To understand this, let’s say you want apple juice, but this time, instead of just juicing it, you also want to put it in a can. So, you’ll need an additional stage where the juice will go through a canning machine.
In representing this, let’s name the juicer $g$, the canning machine $f$, and the freshly picked apple $x$. If we place the apple into the juicer, we’ll get apple juice, represented as $g(x)$. Continuing the process and placing the apple juice through the canning machine, we get the final output of canned apple juice, represented as $f(g(x))$.
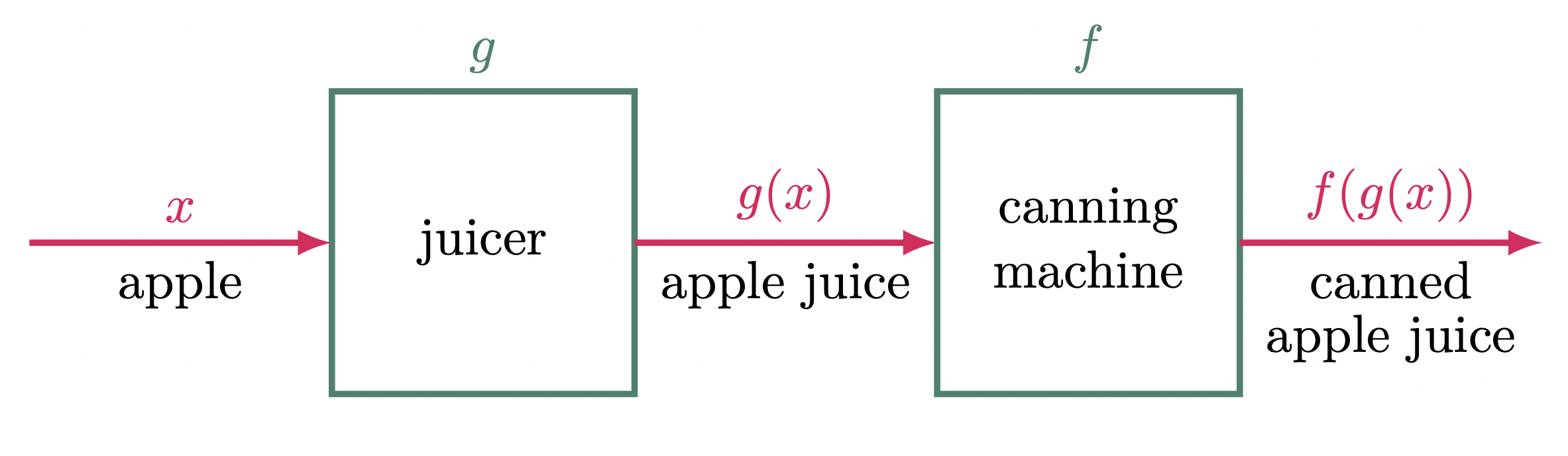
Figure 1
If $f$ and $g$ are both functions of $x$, where $f$ is the outer function and $g$ is the inner function ($f$ is composed with $g$), the composite function is denoted as $(f \circ g)(x)=f(g(x))$, which is read as “$f$ of $g$ of $x$”.
$$\begin{align} (f \circ g)(x)=f(g(x)) \end{align}$$
For example, given two functions $\tcA{f(x)=2x+5}$ and $\tcB{g(x)=3x-4}$, determine $(f \circ g)(x)$
\[\begin{align*} (f \circ g)(x) &= f(g(x)) \end{align*}\]Start with the outer function $f(x)$,
\[\begin{align*} \tcA{f(x)} &\tcA{= 2x+5} \end{align*}\]Then substitute all instances of $x$ with $g(x)$,
\[\begin{align*} \tcA{f(}\tcB{g(x)}\tcA{)} &= \tcA{2(}\tcB{g(x)}\tcA{) + 5} \end{align*}\]Since $g(x)=3x-4$,
\[\begin{align*} \tcA{f(}\tcB{g(x)}\tcA{)} &= \tcA{2(}\tcB{3x-4}\tcA{) + 5} \\ &= 6x-8+5 \\ &= 6x-3 \end{align*}\]Hence, $(f \circ g)= 6x-3$
$\example{1}$ If $ f(x)=x^2 $ and $ g(x)=x+1 $, find: a. $ (f \circ g)(x) $, b. $ (g \circ f)(x) $, c. $ (f \circ f)(x) $, d. $ (g \circ g)(x) $
$\solution$
$\For{a}$
\(\begin{align*}
(f \circ g)(x) &= f(g(x)) \\
f(x) &= x^2 \\
f(g(x)) &= [g(x)]^2 \\
&= (x+1)^2 \\
&= x^2+2x+1 \tagans
\end{align*}\)
$\For{b}$
\(\begin{align*}
(g \circ f)(x) &= g(f(x)) \\
g(x) &= x+1 \\
g(f(x)) &= f(x)+1\\
&= x^2+1 \tagans
\end{align*}\)
$\For{c}$
\(\begin{align*}
(f \circ f)(x) &= f(f(x)) \\
f(x) &= x^2 \\
f(f(x)) &= [f(x)]^2 \\
&= (x^2)^2 \\
&= x^4 \tagans
\end{align*}\)
$\For{d}$
\(\begin{align*}
(g \circ g)(x) &= g(g(x)) \\
g(x) &= x+1 \\
g(g(x)) &= [g(x)]+1 \\
&= (x+1)+1 \\
&= x+2 \tagans
\end{align*}\)
$\example{2}$ If $ g(x)= 2x+1$ and $ h(x)=3-x^2$, find: a. $ g(h(0)) $, b. $ h(g(2)) $, c. $ g(g(-3)) $, d. $ h(h(1/2)) $
$\solution$
$\For{a}$
\(\begin{align*}
g(x) &= 2x+1 \\
g(h(x)) &= 2(3-x^2)+1 \\
g(h(0)) &= 2[3-(0)^2]+1 \\
&= 2(3)+1 \\
&= 7 \tagans
\end{align*}\)
$\For{b}$
\(\begin{align*}
h(x) &= 3-x^2 \\
h(g(x)) &= 3-(2x+1)^2 \\
h(g(2)) &= 3-[2(2)+1]^2 \\
&= 3-(5)^2 \\
&= -22 \tagans
\end{align*}\)
$\For{c}$
\(\begin{align*}
g(x) &= 2x+1 \\
g(g(x)) &= 2(2x+1)+1 \\
g(g(-3)) &= 2[2(-3)+1]+1 \\
&= 2(-5)+1 \\
&= -9 \tagans
\end{align*}\)
$\For{d}$
\(\begin{align*}
h(x) &= 3-x^2 \\
h(h(x)) &= 3-(3-x^2)^2 \\
h(h(1/2)) &= 3-[3-(1/2)^2]^2 \\
&= 3-\br{ 3-\frac{1}{4} }^2 \\
&= 3-\br{ \frac{11}{4} }^2 \\
&= -\frac{73}{16} \tagans
\end{align*}\)
$\example{3}$ If $ f(x)=x+3$, $ g(x)=(x+1)^2$ and $ h(x)=\frac{1}{x}$, find: a. $ f(g(h(x))) $, b. $ g(h(f(x))) $, c. $ h(f(g(2))) $, d. $ h(g(f(x))) $, e. $ f(h(g(x))) $, f. $ g(f(h(1/2))) $
$\solution$
$\For{a}$
\(\begin{align*}
f(x) &= x+3 \\
f(g(x)) &= (x+1)^2+3 \\
f(g(h(x))) &= \br{ \frac{1}{x}+1 }^2+3 \\
&= \br{ \frac{1}{x^2}+\frac{2}{x}+1 }+3 \\
&= \frac{1}{x^2}+\frac{2}{x}+4 \tagans
\end{align*}\)
$\For{b}$
\(\begin{align*}
g(x) &= (x+1)^2 \\
g(h(x)) &= \br{ \frac{1}{x}+1 }^2 \\
g(h(f(x))) &= \br{ \frac{1}{x+3}+1 }^2 \\
&= \br{ \frac{1}{x+3}+\frac{x+3}{x+3} }^2 \\
&= \br{ \frac{x+4}{x+3} }^2 \\
&= \frac{(x+4)^2}{(x+3)^2} \tagans
\end{align*}\)
$\For{c}$
\(\begin{align*}
h(x) &= \frac{1}{x} \\
h(f(x)) &= \frac{1}{x+3} \\
h(f(g(x))) &= \frac{1}{(x+1)^2+3} \\
h(f(g(2))) &= \frac{1}{(2+1)^2+3} \\
&= \frac{1}{12} \tagans
\end{align*}\)
$\For{d}$
\(\begin{align*}
h(x) &= \frac{1}{x} \\
h(g(x)) &= \frac{1}{(x+1)^2} \\
h(g(f(x))) &= \frac{1}{[(x+3)+1]^2} \\
&= \frac{1}{(x+4)^2} \tagans
\end{align*}\)
$\For{e}$
\(\begin{align*}
f(x) &= x+3 \\
f(h(x)) &= \frac{1}{x}+3 \\
f(h(g(x))) &= \frac{1}{(x+1)^2}+3 \\
&= \frac{1+3(x+1)^2}{(x+1)^2} \\
&= \frac{1+3(x^2+2x+1)}{\left(x+1\right)^2} \\
&= \frac{3x^2+6x+4}{\left(x+1\right)^2} \tagans
\end{align*}\)
$\For{f}$
\(\begin{align*}
g(x) &= (x+1)^2 \\
g(f(x)) &= (x+3+1)^2 \\
g(f(h(x))) &= \br{ \frac{1}{x}+4 }^2 \\
g(f(h(1/2))) &= \br{ \frac{1}{\frac{1}{2}}+4 }^2 \\
&= (2+4)^2 \\
&= 36 \tagans
\end{align*}\)
$\example{4}$ If $ f(x)= \frac{2}{x+1}$ and $ f(g(x))=x$, determine $g(x)$.
$\solution$
In this case, the composed function is one of the given,
\(\begin{align*}
f(g(x)) &= x
\end{align*}\)
Start with $f(x)$
\[\begin{align*} f(x) &= \frac{2}{x+1} \\ f(g(x)) &= \frac{2}{ g(x) +1} \end{align*}\]Since $f(g(x))=x$,
\[\begin{align*} \frac{2}{ g(x) +1} &= x \\ g(x) +1 &= \frac{2}{x} \\ g(x) &= \frac{2}{x} -1 \tag*{(ans.)} \end{align*}\]You can check your answer by composing the function,
\[\begin{align*} f(x) &= \frac{2}{x+1} \\ f(g(x)) &= \frac{2}{\br{ \frac{2}{x} -1 }+1} \\ &= \frac{2}{\frac{2}{x}} \\ &= x \end{align*}\]
