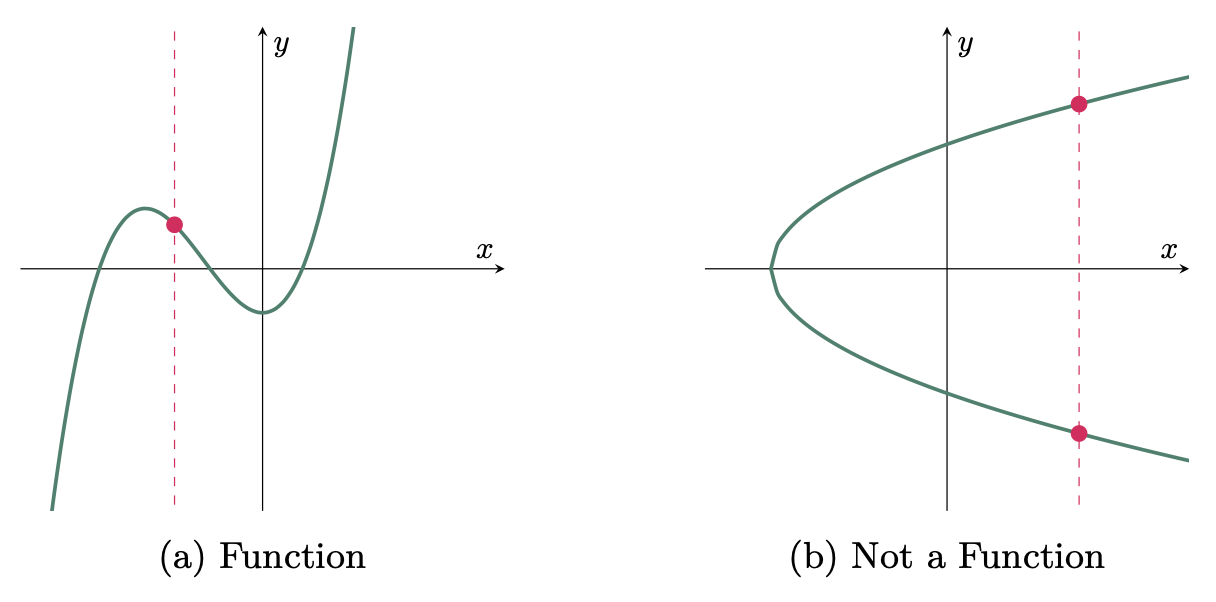
From our past lesson, we have already learned how to determine if an equation represents a function or not. In this section, let us discuss how to determine if a graph represents a function or not using the Vertical Line Test.
The method is relatively straightforward. If we can draw a vertical line that intersects the graph more than once, the graph is considered NOT A FUNCTION since a function must only have a single output for every input. Furthermore, the number of intersections of the graph and the vertical line represents the number of outputs the graph has at a specific input.
$\example{1}$ Determine if the given curve represents a function or not.
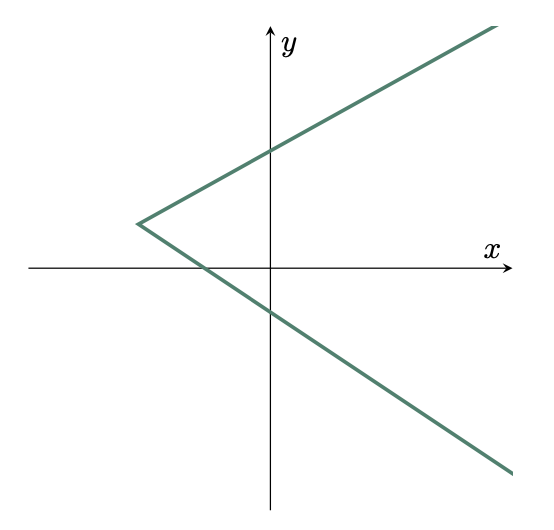
$\solution$
Use the Vertical Line Test,
Since the vertical line intersects the graph more than once, it is NOT A FUNCTION.
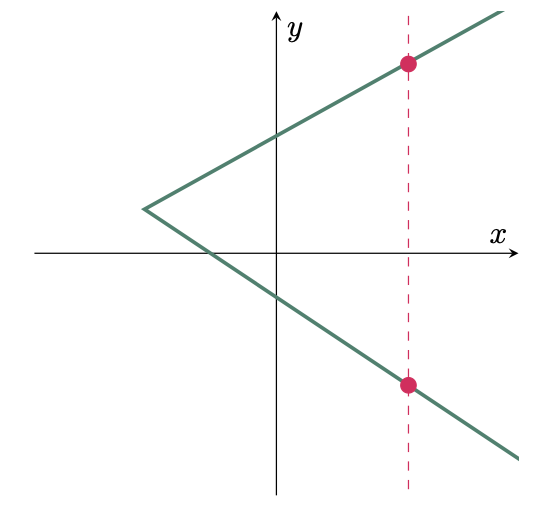
$\example{2}$ Determine if the given curve represents a function or not.
$\solution$
Use the Vertical Line Test,
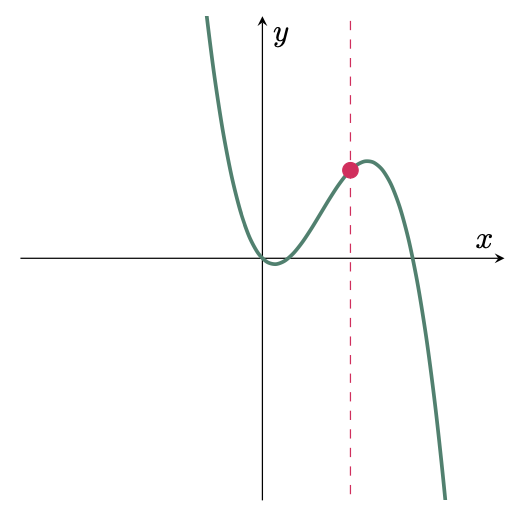
Since the vertical line intersects the graph at only one point, it is a FUNCTION.
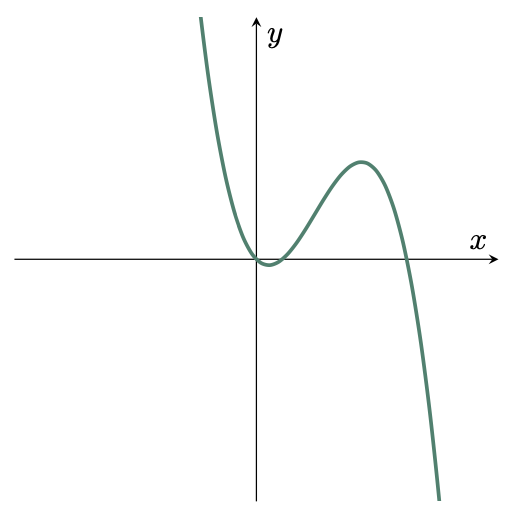
$\example{3}$ Determine if the given curve represents a function or not.
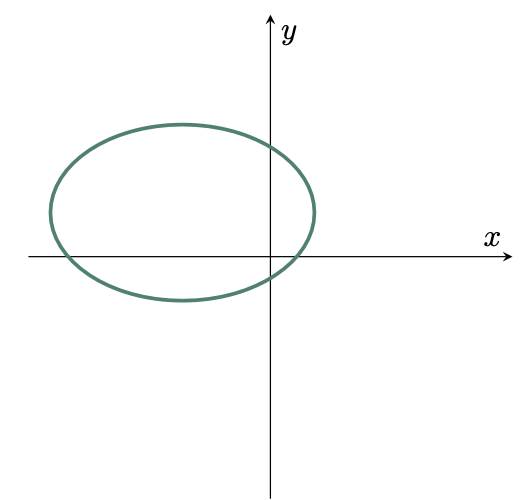
$\solution$
Use the Vertical Line Test,
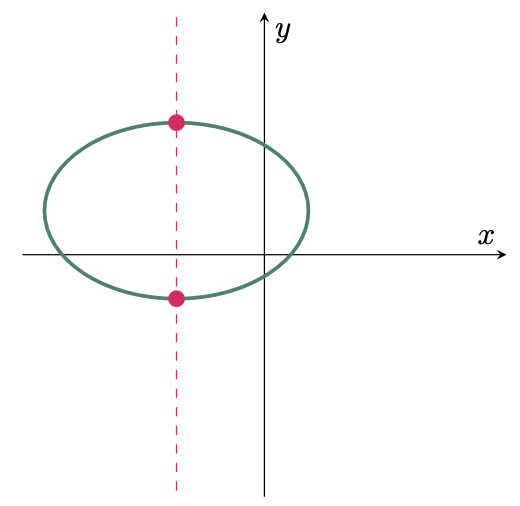
Since the vertical line intersects the graph more than once, it is NOT A FUNCTION.