We can evaluate functions by interpreting its graph. From our past lesson, we already have learned about Function Notation as well as the placement of each variable on the Cartesian Plane. To review, the input can be located inside the parenthesis in Function Notation or the Horizontal Axis on the Cartesian Plane. On the other hand, the output is on the other side of the equation in Function Notation or on the Vertical Axis on the Cartesian Plane.
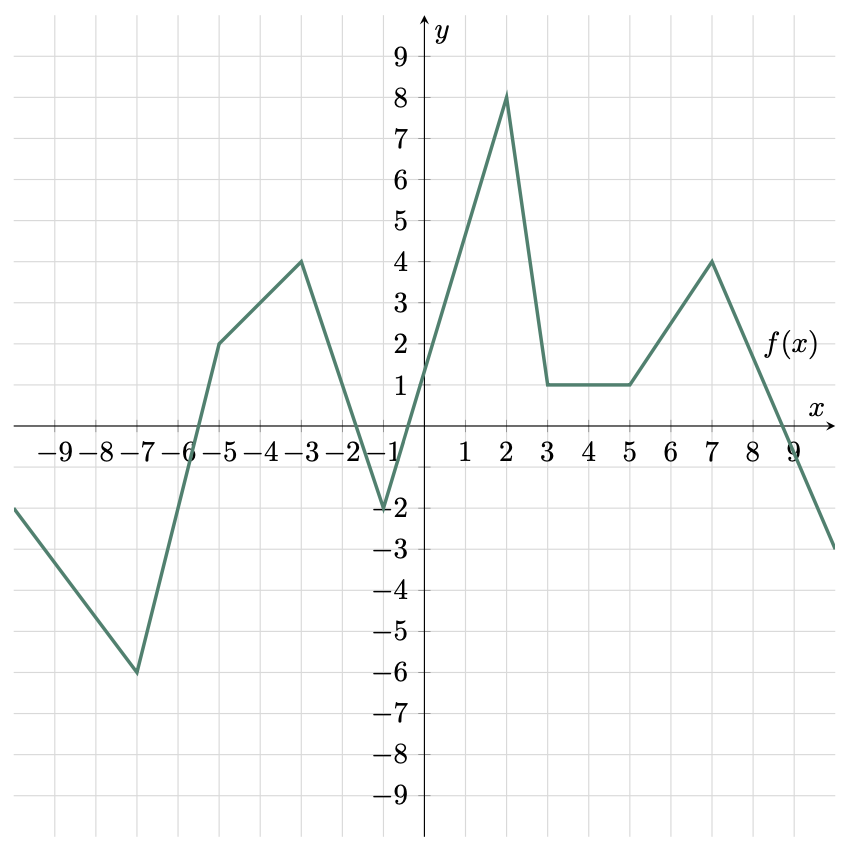
$\example{1}$ From the given graph, find: a. $ f(2) $, b. $ f(5) $, c. $ f(-6) $, d. $ f(-4) $
$\solution$
To evaluate functions from a graph, remember that $y=f(x)$, so $f(2)$ means that the $x$-coordinate is 2, and if we substitute it to the function we would get its $y$-coordinate. See the figure below.
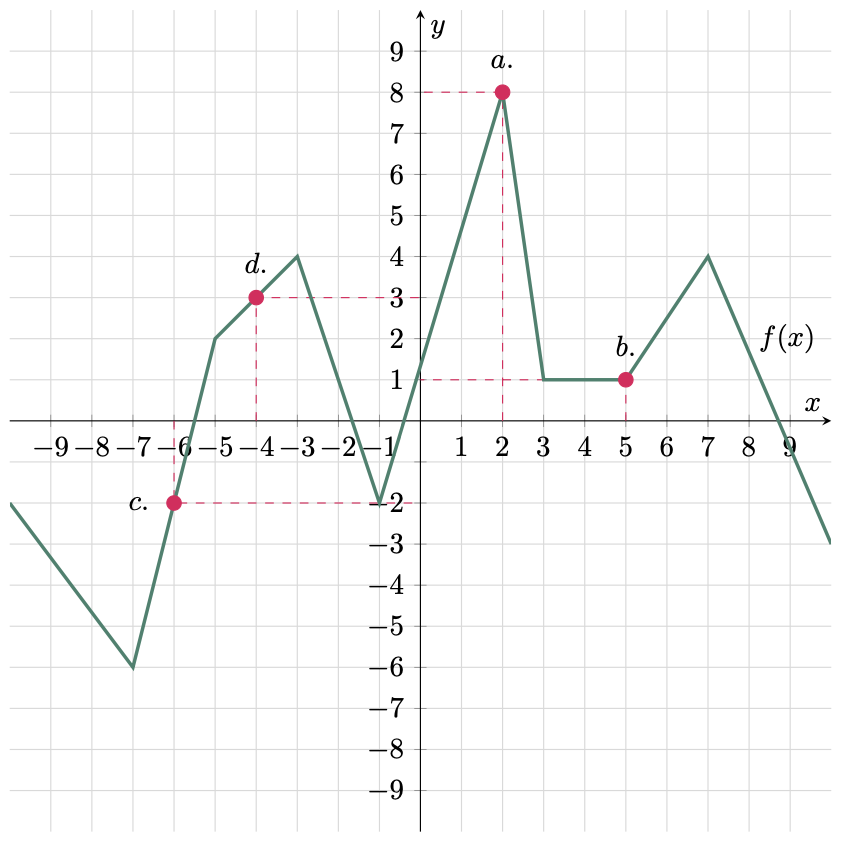
Hence,
a. $ f(2) =8$
b. $ f(5) =1$
c. $ f(-6) =-2$
d. $ f(-4) =3$
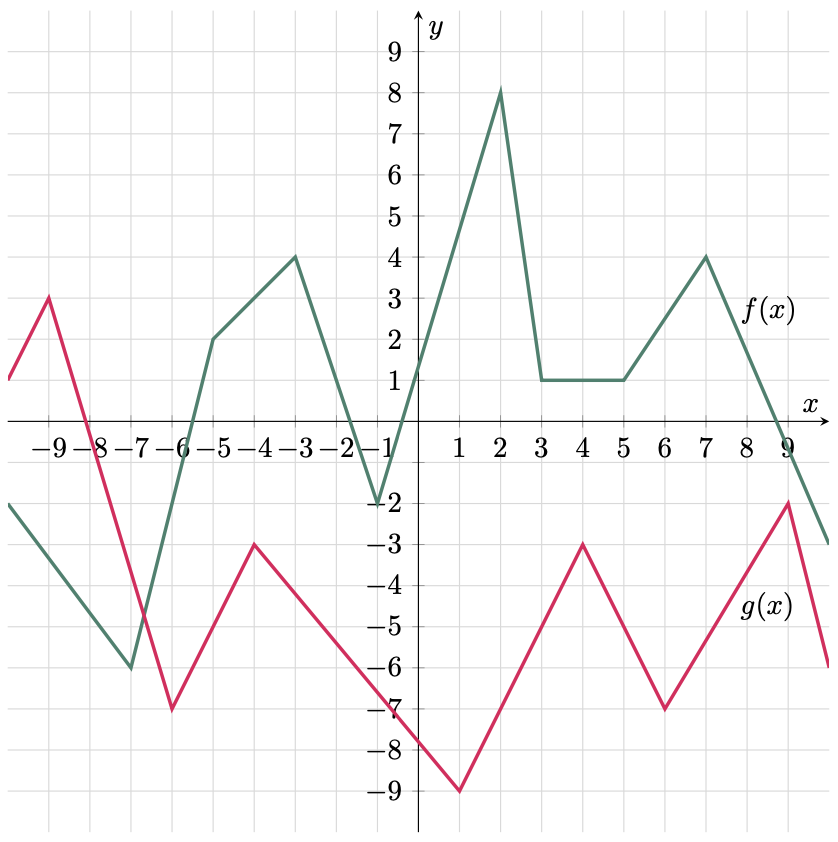
$\example{2}$ From the given graph, find: a. $ f(3)+g(4) $, b. $ (f-g)(5) $, c. $ 5[g(9)] + 2[f(-4)] $, d. $ 7[(g\cdot f)(-6)] $
$\solution$
In this problem, the solution is similar to the previous example. However, we will only be applying an additional competency that we have learned in the Combination of Functions.
$\For{a}$
\(\begin{align*}
f(3)+g(4) &= 1+(-3) \\
&= 1-3 \\
&= -2 \tagans
\end{align*}\)
$\For{b}$
\(\begin{align*}
(f-g)(5) &= f(5)-g(5) \\
&= 1-(-5) \\
&= 1+5 \\
&= 6 \tagans
\end{align*}\)
$\For{c}$
\(\begin{align*}
5[g(9)] + 2[f(-4)] &= 5[-2]+2[3] \\
&= -10+6 \\
&= -4 \tagans
\end{align*}\)
$\For{b}$
\(\begin{align*}
7[(g\cdot f)(-6)] &= 7[g(-6) \cdot f(-6)] \\
&= 7[(-7)\cdot (-2)] \\
&= 7(14) \\
&= 98 \tagans
\end{align*}\)