Odd and Even functions can be easily determined graphically based on its symmetry. A function is considered “even” if its graph is symmetrical with respect to the $y$-axis or the graph is reflected at the other side of the $y$-axis, while a function is considered as an “odd” function if its graph is symmetrical with respect to the origin.
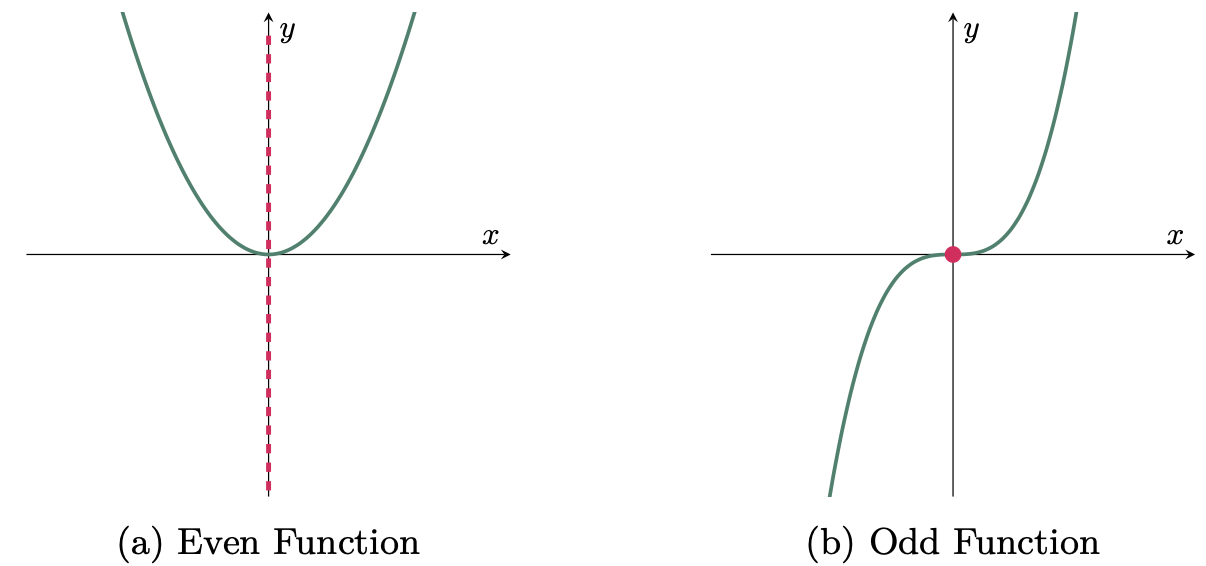
Having the knowledge if a function is Odd or Even is a great help in graphing the function, since we’ll be able to know its symmetry. In order to identify algebraically if a function is odd, even or neither, we need to replace $x$ with $-x$ in the function. If the result is equal to the original function, then the function is even; if it is the negative of the original function, then the function is odd; and if it is not of the two, then the function is neither odd nor even.
$$\begin{align} \text{Even Function} && f(-x)&=f(x) \label{eq:even function}\\ \text{Odd Function} && f(-x)&=-f(x) \label{eq:odd function} \end{align}$$
$\example{1}$ Determine whether the function $f(x)=x^4+2x^2-3$ is odd, even, or neither
$\solution$
Replace $x$ with $-x$,
\[\begin{align*} f(-x) &= (-x)^4+2(-x)^2-3 \\ &= x^4+2x^2-3 \end{align*}\]Since $f(x)=x^4+2x^2-3$,
\[\begin{align*} f(-x) &= f(x) \end{align*}\]Hence, the function is Even
$\example{2}$ Determine whether the function $g(x)=5x^3-3x$ is odd, even, or neither
$\solution$
Replace $x$ with $-x$,
\[\begin{align*} g(-x) &= 5(-x)^3-3(-x) \\ &= -5x^3+3x \\ &= -(5x^3-3x) \\ \end{align*}\]Since $g(x)=5x^3-3x$,
\[\begin{align*} g(-x) &=-g(x) \end{align*}\]Hence, the function is Odd
$\example{3}$ Determine whether the function $\phi(x)=-2x^5+2x^3$ is odd, even, or neither
$\solution$
Replace $x$ with $-x$,
\[\begin{align*} \phi(-x) &= -2(-x)^5+2(-x)^3 \\ &= 2x^5-2x^3 \\ &= -(-2x^5+2x^3) \\ \end{align*}\]Since $\phi(x)=-2x^5+2x^3$,
\[\begin{align*} \phi(-x) &= -\phi(x) \end{align*}\]Hence, the function is Odd
$\example{4}$ Determine whether the function $F(x)=\frac{8}{x^2+3}$ is odd, even, or neither
$\solution$
Replace $x$ with $-x$,
\[\begin{align*} F(-x) &= \frac{8}{(-x)^2+3} \\ &= \frac{8}{x^2+3} \\ F(-x) &= F(x) \end{align*}\]Hence, the function is Even
$\example{5}$ Determine whether $h(x)=2x^3-x^2-5x+2$ is odd, even, or neither
$\solution$
Replace $x$ with $-x$,
\[\begin{align*} h(-x) &= 2x^3-x^2-5x+2 \\ &= 2(-x)^3-(-x)^2-5(-x)+2 \\ &= -2x^3-x^2+5x+2 \end{align*}\]$h(-x) \neq h(x)$ and $h(-x) \neq -h(x)$ hence, the function is neither odd nor even