The concept of limits may be new to you, but this is one of the basic foundations of calculus, distinguishing it from all the prerequisite mathematics you might have already undergone. Thus, in order to fully grasp the notions that we will soon encounter, we must first fully understand this topic.
Let’s start with a visual representation of what a limit is. Imagine you’re crossing a bridge $AB$ (see Figure 1), and you’re only allowed to move half of your current location starting at point $A$. With this, no matter how hard you strive to get to point $B$, you will never be at the exact point. But, yes, you’ll be able to get close enough to appear as if you’re stepping at point $B$. With this in mind, you’re approaching relatively close to point $B$ without actually getting there. Therefore, we can say that your limit is at point $B$.
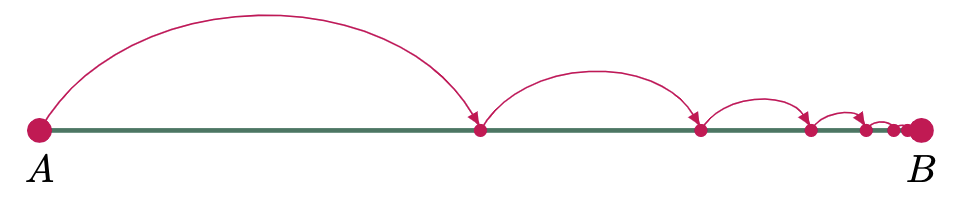
Figure 1: Visual Presentation of Limits
Notation of Limits
Before attempting to answer problems in Limits, it is necessary to familiarize ourselves with its notation. Consider $f(x)$ as a function of $x$ and $a$ as a constant. In order for the function $f(x)$ to get relatively close to the Limit $L$, $x$ must be sufficiently close to $a$. This is denoted as,
$$\begin{align} \lim_{x \to a}{f(x)} = L \end{align}$$
which is read “the limit of the function of $x$, as $x$ approaches $a$ is $L$’’. This can also be presented as,
$$\begin{align} f(x) \to L , \, \text{as} \, x \to a \end{align}$$
which is read “$f(x)$ approaches $L$, as $x$ approaches $a$”
To illustrate this, let us attempt to solve a few problems.
$\example{1}$ Evaluate, $\lim\limits_{x \to 3}{(x-1)} $
$\solution$
In evaluating limits, it is best first to try to substitute the value of $a$ to the function. In this case, if we replace $x$ with 3, we end up with a value.
\[\begin{align*} \lim_{x \to 3}{(x-1)} &= 3-1\\ &= 2 \tagans \end{align*}\]But let’s try to solve this using the definition of what a limit is by assigning values to $x$ that approaches $3$ from either sides:

Graphing the function gives us,
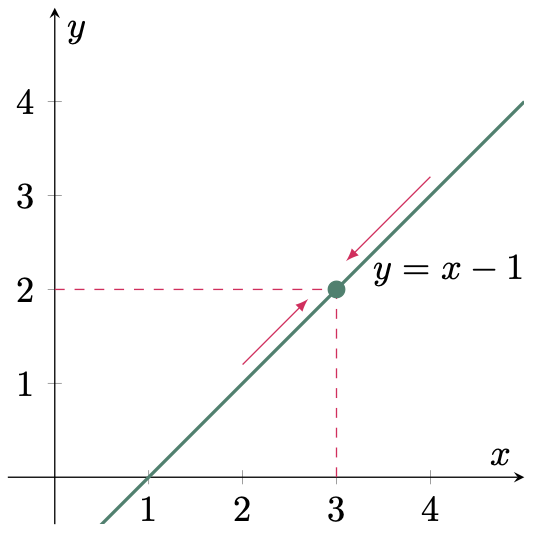
As $x$ approaches 3 from either sides, the function approaches to 2, and when $x$ is equal to 3, the function is also equal to 2. But you might ask yourself “what is the use of limits if it just behaves the same as a function’’. Yes, in this example $f(3)=2$, but this is not always the case, to further understand what a limit is, let us solve for the next problem.
$\example{2}$ Evaluate, $\lim_{x \to 2} \frac{x^2-4}{x-2} $
$\solution$
By substituting $x$ to the function with $2$, the result will be $\frac{4-4}{2-2}= \frac{0}{0} $, which is undefined. With this in mind, let us assign values to $x$ that approaches $2$ from either sides,

We can now plot the graph, where the function is defined for all real numbers except when $x=2$.
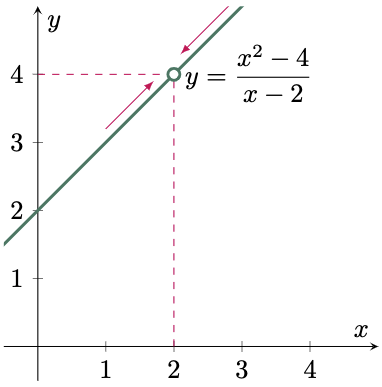
The figure shows that the function approaches 4 as $x$ approaches 2 from either sides (left or right), except when $x$ is exactly equal to 2 where the function is undefined. But since a limit mostly cares about what it approaches regardless of the destination, we can say that the limit of the function is 4.
You can also try interacting with the graph above. If you try hovering your cursor close to $x=2$, you will get a value for $y$. However, when you arrive at EXACTLY $x=2$, the value of your $y$-component is undefined. This shows that even if $f(2)$ is undefined, we are still approaching a specific value, which is 4.
Furthermore, the limit of this type of function can also be solved by simplifying the function first before substituting the value to the equation,
\[\begin{align*} \lim_{x \to 2} \frac{x^2-4}{x-2} &= \lim_{x \to 2} \frac{(x+2) \cancel{(x-2)} }{ \cancel{x-2} } \\ &= \lim_{x \to 2} {x+2} \\ &= 2+2 \\ &= 4 \tagans \end{align*}\]
