Infinity is a mathematical concept that describes anything that has no bounds and is usually denoted by the symbol “$\infty$”. Infinity can specify an infinitely large or infinitely small quantity, and a positive “$+$” or negative “$-$” sign is written before the infinity symbol to indicate its direction on the number line.

Figure 1: Number Line
Limits at Infinity of a Fraction
Consider a pizza sliced into 8 equal parts (Figure 2a), each one will get $\frac{1}{8}$ or 0.125 part of the pizza. If it is sliced to 50 parts, each will get $\frac{1}{50}$ or 0.02 part of the pizza (Figure 2b). And as the number of slices $x$ increases, the size of each slice $n$ decreases. Hence, $x$ and $n$ are inversely proportional to each other $\frac{1}{x}=n$.
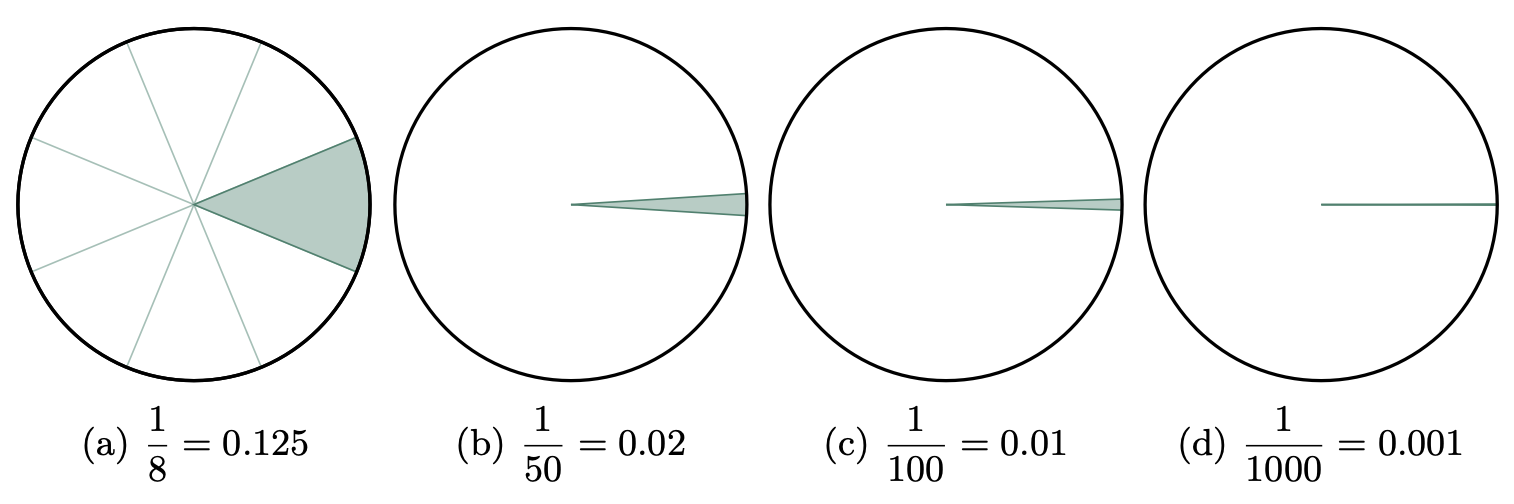
Figure 2: Pizza Slice
So, if the pizza is divided into infinite pieces, the size of each slice cannot be simply measured since $\frac{1}{\infty}$ is undefined. But if we use the concept of limits and approach the number of slices to infinity, the size of each piece will approach zero.
\[\lim\limits_{x \to \infty}\frac{1}{x}=0\]This can also be shown by graphing the function $y =\frac{1}{x}$ (Figure 3), which denotes not only as $x$ approaches infinity is equal to zero, but also as $x$ approaches negative infinity.
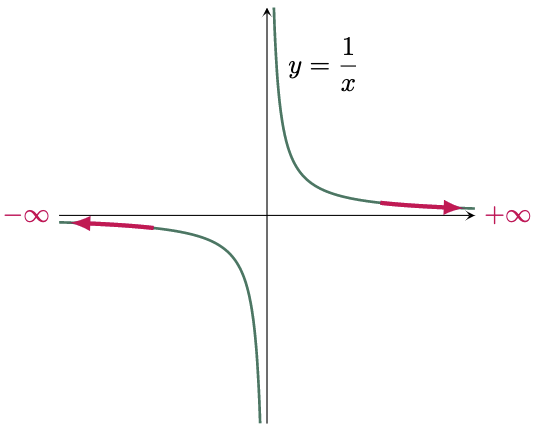
Figure 3: Graphical representation of $f(x)=\frac1x$
$$\begin{align} \lim\limits_{x \to \infty}\frac{1}{x}=\lim\limits_{x \to -\infty}\frac{1}{x}=\lim\limits_{x \to \pm\infty}\frac{1}{x}=0 \label{eq:limits at infinity of a fraction} \end{align}$$
$\example{}$
Evaluate the following limits:
a. $\lim\limits_{x\to\infty}\frac{7}{x}$
b. $\lim\limits_{x\to-\infty}\frac{7}{x}$
$\solution$
$\For{a}$
Factor the expression,
Since $\lim\limits_{x \to\infty}\frac{1}{x}=0$,
\[\begin{align*} &= 7(0) \\ &= 0 \tagans \end{align*}\]$\For{b}$
Since, $\lim\limits_{x \to\pm\infty}\frac{1}{x}=0$. Whether $x$ approaches to infinity or negative infinity, the answer would still be the same.
$\example{2}$
Evaluate the following limits:
a. $\lim\limits_{x\to\infty} \frac{25}{3x^3}$
b. $\lim\limits_{x\to-\infty} \frac{25}{3x^3}$
$\solution$
$\For{a}$
Factor the expression,
$\For{b}$
As you have noticed, as long as $x$ or any multiple of $x$ is the denominator of the function, its limit as $x$ approaches to either positive or negative infinity is always zero. Thus,
$\example{3}$ Evaluate the limit, $\lim\limits_{x\to\infty} \frac{20x-6}{x}$
$\solution$
Simplify the expression,
\[\begin{align*} \lim\limits_{x\to\infty} \frac{20x-6}{x} &= \lim\limits_{x\to\infty} \br{ \frac{20x}{x}-\frac{6}{x} } \\ &= \lim\limits_{x\to\infty} \br{ 20-\frac{6}{x} } \\ &= 20-0\\ &=20 \tagans \end{align*}\]Limits at Infinity of Polynomials
The limit of any polynomial as $x$ approaches $\pm\infty$ has a limit of positive or negative infinity $\pm\infty$, where the sign of the limit will depend on the leading term $ax^n$. Since it bears the largest exponent, $x^n$ increases (or decreases if its negative) much faster compared to the other terms.
$$\begin{align} \lim\limits_{x \to \pm\infty}(ax^n+bx^{n-1}+cx^{n-2}+\cdots)=\pm\infty \label{eq:limits at infinity of a polynomial} \end{align}$$
$\example{4}$
Evaluate the following limits:
a. $\lim\limits_{x\to\infty} (7x^2)$
b. $\lim\limits_{x\to-\infty} (7x^2)$
$\solution$
$\For{a}$
\[\begin{align*} \lim\limits_{x\to\infty} (7x^2) &= 7(\infty)^2 \\ \end{align*}\]Squaring infinity would result to a larger infinity, which is still infinity.
\[\begin{align*} \phantom{aaaaa} &= 7(\infty) \\ \end{align*}\]And any number multiplied to infinity would become insignificant. Thus,
\[\begin{align*} \lim\limits_{x\to\infty} (7x^2) &= \infty \tagans \end{align*}\]$\For{b}$
\[\begin{align*} \lim\limits_{x\to-\infty} (7x^2) &= 7(-\infty)^2 \\ \end{align*}\]Squaring any negative number would result to positive. Thus,
\[\begin{align*} &= 7(\infty) \\ &= \infty \tagans \end{align*}\]$\example{5}$
Evaluate the following limits:
a. $\lim\limits_{x\to\infty} (7x+2-x^3)$
b. $\lim\limits_{x\to-\infty} (7x+2-x^3)$
$\solution$
$\For{a}$
In this example, the leading term is $-x^3$ since its exponent has the highest power. With this, all the other terms would become insignificant. Hence, we can focus our attention to this term.
$\For{b}$
\[\begin{align*} \lim\limits_{x\to-\infty} (7x+2-x^3) &= \lim\limits_{x\to\infty} (\cancel{7x}+\cancel{2}-x^3) \\ &= \lim\limits_{x\to-\infty} (-x^3)\\ &= -(-\infty)^3 \\ &= -(-\infty) \\ &= \infty \tagans \end{align*}\]$\example{6}$
Evaluate the following limits:
a. $\lim\limits_{x\to\infty} (-20x^{-7}+3x^{-5})$
b. $\lim\limits_{x\to-\infty} (-20x^{-7}+3x^{-5})$
$\solution$
$\For{a}$
In this example, all the variables contains negative exponents. So,
$\For{b}$
\[\begin{align*} \lim\limits_{x\to-\infty} (-20x^{-7}+3x^{-5}) &= \lim\limits_{x\to-\infty} \br{ -\frac{20}{x^7}+\frac{3}{x^5} } \\ &= \lim\limits_{x\to-\infty} \br{ -\frac{20}{x^7}}+\lim\limits_{x\to-\infty} \br{\frac{3}{x^5} } \\ &= 0+0 \\ &= 0 \tagans \end{align*}\]Limits at Infinity of Rational Functions
Evaluating the limits of a rational function may require an extra step or two before determining its result. However, with a bit of help from algebra, we can transform the function in such a way that we can use Equation 1 or 2 to determine its limit.
First, we can divide both the numerator and the denominator by the variable with the highest exponent found on the denominator. With this, we can eliminate some of the terms by using Equation 1 to the terms that have a variable for their denominator. Furthermore, the limit of the function will still vary depending on the degree of the numerator and denominator.
$\example{7}$ Evaluate the limit, $\lim\limits_{x\to\infty} \frac{3x^4+4x-2}{7+2x^4}$.
$\solution$
Start by dividing both the numerator and the denominator by the variable with the highest power, which in this case is $x^4$
\[\begin{align*} \lim\limits_{x\to\infty} \frac{3x^4+4x-2}{7+x^4} &= \lim\limits_{x\to\infty} \frac{(3x^4/x^4)+(4x/x^4)-(2/x^4)}{(7/x^4)+(2x^4/x^4)} \\ &= \lim\limits_{x\to\infty} \frac{3+(4/x^3)-(2/x^4)}{(7/x^4)+2} \\ \end{align*}\]Since, $\lim\limits_{x\to\pm\infty} \frac{1}{x}=0$
\[\begin{align*} &= \lim\limits_{x\to\infty} \frac{3+\cancelto{0}{(4/x^3)}-\cancelto{0}{(2/x^4)}}{\cancelto{0}{(7/x^4)}+2} \\ &= \frac{3+0-0}{0+2} \\ &= \frac{3}{2} \tagans \end{align*}\]$\example{8}$ Evaluate the limit, $\lim\limits_{x\to-\infty} \frac{3x+4}{5x^2-7}$.
$\solution$
Divide the numerator and the denominator by $x^2$,
\[\begin{align*} \lim\limits_{x\to-\infty} \frac{3x+4}{5x^2-7} &= \lim\limits_{x\to-\infty} \frac{(3x/x^2)+(4/x^2)}{(5x^2/x^2)-(7/x^2)} \\ &= \lim\limits_{x\to-\infty} \frac{(3/x)+(4/x^2)}{5-(7/x^2)} \\ &= \frac{0+0}{5-0} \\ &= 0 \tagans \end{align*}\]$\example{9}$ Evaluate the following limits of the function $f(x)=\frac{x^3-2x}{5x^2+1}$ as $x$ approaches (a) infinity, and (b) negative infinity.
$\solution$
$\For{a}$
For cases that the degree of the denominator is greater than the numerator, divide the numerator and the denominator by the variable with the highest power found on the denominator, which in this case is $x^2$
$\For{b}$
\[\begin{align*} \lim\limits_{x\to-\infty} \frac{x^3-2x}{5x^2+1} &= \lim\limits_{x\to-\infty} \frac{(x^3/x^2)-(2x/x^2)}{(5x^2/x^2)+(1/x^2)} \\ &= \lim\limits_{x\to-\infty} \frac{(x)-\cancelto{0}{(2/x)}}{(5)+\cancelto{0}{(1/x^2)}} \\ &= \frac{1}{5}(-\infty) \\ &= -\infty \tagans \end{align*}\]
