In our previous lessons, we gradually introduced the notion of limits, beginning with approximating values and progressing to topics involving infinity. In this lesson, we will be introducing One-sided limits. As the name suggests, one-sided limits are concerned with the limit that approaches from only one side, either from the right side or the left side of the given function. To truly grasp how one-sided limits can be beneficial, let us look at some situations in a graphical representation.
Consider the graph in (Figure 1a), it shows that as $x$ approaches $a$ from the left side, the function approaches 3, and as $x$ approaches $a$ from the right side, the function approaches 1. This illustrates how limits might differ depending on which side of the function is approaching. This type of limit is called a One-sided limit. It focuses on only one side of the limit, which is where the function approaches. As a result, one-sided limits can be classified into two types: left-hand limits and right-hand limits. The two limits are dealt with independently. Furthermore, there are some instances that there may be only one limit present representing one side of the function (see Figures 1b and 1c).
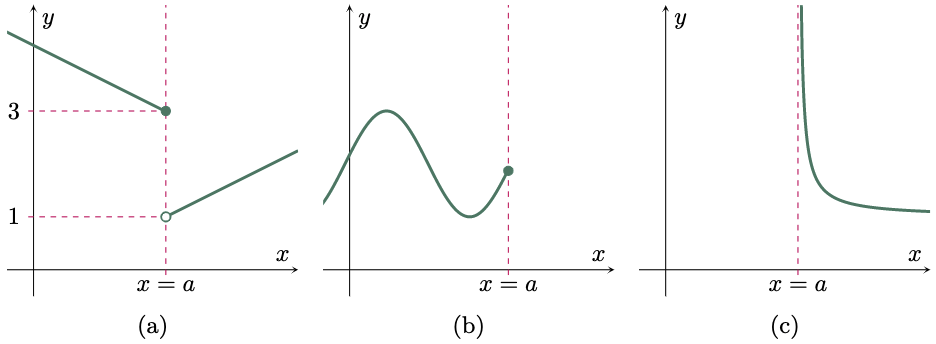
Figure 1: The function in (a) has different limits on each sides, in (b) only left-hand limit exist, and in (c) only right-hand limit exist
Right-hand Limit
Right-hand limit is where $x$ approaches $a$ from the right or approaches from values greater than $a$. An exponent of positive sign “$+$” is used to represent this notation, which tells that $x$ must be larger than $a$ “$x>a$”. Hence, right-hand limit is denoted as,
$$\begin{align} \lim\limits_{x \to a^{+}}{f(x)}=L \end{align}$$
Which is read as “the limit of the function $f(x)$ as $x$ approaches $a$ from the right is $L$.”
Left-hand Limit
Left-hand limit is where $x$ approaches $a$ from the left or approaches from values less than $a$. An exponent of negative sign “$-$” is used to represent this notation, which tells that $x$ must be less than $a$ “$x<a$”. Hence, left-hand limit is denoted as,
$$\begin{align} \lim\limits_{x \to a^{-}}{f(x)}=L \end{align}$$
Which is read as “the limit of the function $f(x)$ as $x$ approaches $a$ from the left is $L$.”
Two-sided Limit
If the left and right hand limits of a function are both approaching to the same value, then it is considered as two-sided limits or ordinary limits, which we have already discussed at the beginning of this chapter.
$$\begin{align} \lim_{x\to a}f(x)=\lim_{x\to a^-}{f(x)} = \lim_{x\to a^+}{f(x)} \label{eq:two sided limits} \end{align}$$
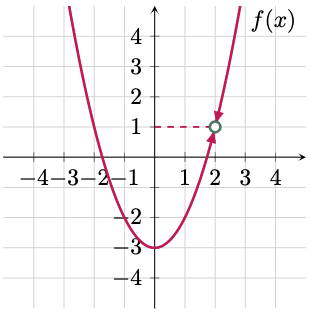
$\example{1}$
Evaluate the following limits based from the graph.
a. $\lim_{x \to 2^-}f(x)$
b. $\lim_{x \to 2^+}f(x)$
c. $\lim_{x \to 2}f(x)$
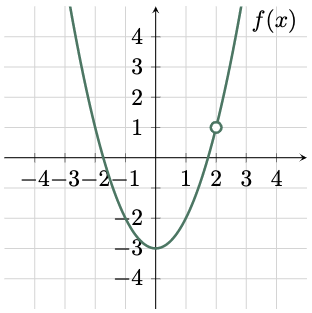
$\solution$
$\For{a}$
To evaluate the left-hand limit of the function as $x$ approaches $2^-$, trace the graph from the left side of $x=2$. Then determine the corresponding output value, which in this case is 1. Hence,
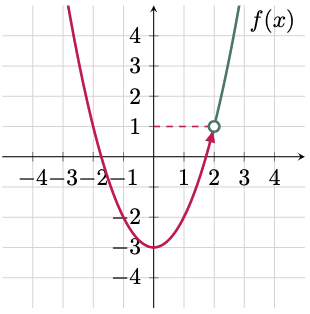
$\For{b}$
To evaluate the \tcA{right-hand limit} of the function as $x$ approaches $2^+$, trace the graph from the \tcA{right side} of $x=2$. Then determine the corresponding output value, which in this case is also 1. Hence,
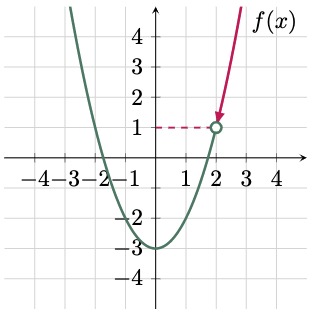
$\For{c}$
Since both the left and right hand limits approaches the same value at $x=2$. Use Equation 3,
$\example{2}$
Evaluate the following limits based from the graph.
a. $\lim_{x \to 1^-}f(x)$
b. $\lim_{x \to 1^+}f(x)$
c. $\lim_{x \to 1}f(x)$
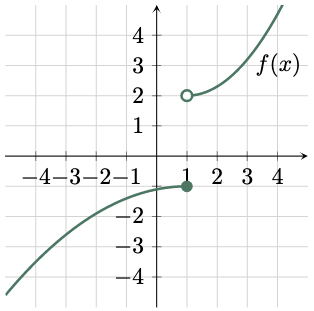
$\solution$
$\For{a}$
To evaluate the left-hand limit of the function as $x$ approaches $1^-$, trace the graph from the left side of $x=1$. Then determine the corresponding output value, which in this case is $-1$. Hence,
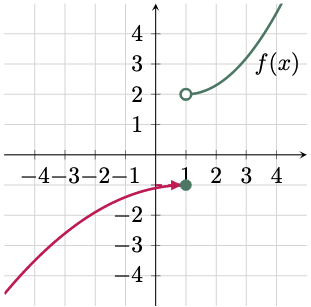
$\For{b}$
To evaluate the right-hand limit of the function as $x$ approaches $1^+$, trace the graph from the right side of $x=1$. Then determine the corresponding output value, which in this case is 2. Hence,
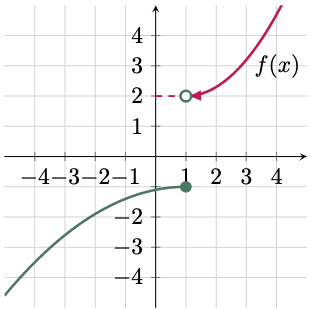
$\For{c}$
Since the left and the right hand limits approaches to different values, the limit of the function as $x$ approaches 1 does not exist (DNE).
$\example{3}$
Evaluate the following limits based from the graph.
a. $\lim_{x \to -2^-}f(x)$
b. $\lim_{x \to -2^+}f(x)$
c. $\lim_{x \to -2}f(x)$
d. $\lim_{x \to 3^-}f(x)$
e. $\lim_{x \to 3^+}f(x)$
f. $\lim_{x \to 3}f(x)$
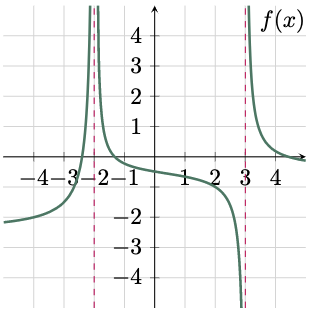
$\solution$
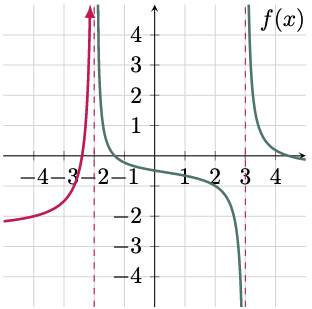
$\For{a}$
To evaluate the left-hand limit of the function as $x$ approaches $-2^-$, trace the graph from the left side of $x=-2$. In this case, the function is approaching to positive infinity. Hence,
$\For{b}$
Tracing the graph from the right side of $x=-2$ also leads to positive infinity. Hence,
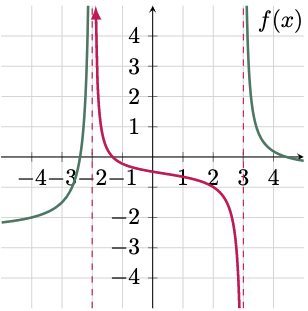
$\For{c}$
Since both the left and right hand limits approaches to the same value as $x$ approaches $-2$,
$\For{d}$
Tracing the graph from the left side of $x=3$ leads to negative infinity.
Hence,
$\For{e}$
Tracing the graph from the right side of $x=3$ leads to positive infinity.
Hence,
$\For{f}$
Since the left and the right hand limits approaches to different values, the limit of the function as $x$ approaches 3 does not exist (DNE).

