Let us begin our lesson with reviewing the concept of absolute value. Absolute value or sometimes called the modulus is the distance from zero in the number line. Since it only measures the distance, the resulting value will always be non-negative.
Simply put, the absolute value removes the negative sign of a number. So, for instance, the absolute value of $-5$ is $5$, and the absolute value of $5$ is also $5$.
\[\begin{align*} |-5| &= 5 \\ |5| &= 5 \end{align*}\]With this in mind, it is possible to breakdown a function with an absolute value. Bear in mind that an absolute value can contain two possible input values, as its primary purpose is to eliminate the negative sign. Given this, both positive and negative values of the function contained within the absolute value symbol are possible. Thus, we can express the absolute value of $x$ as,
\[|x|= \begin{cases} x, & \text{if $x \geq 0$} \\ -x, & \text{if $x<0$} \end{cases}\]By examining each of these cases separately, we can establish how the function acts to the left and right of $x=a$ by using the concept of One-Sided Limits. Furthermore, we can now find the limit as $x$ approaches $a$ by combining the two independent limits. To illustrate this, let us have some examples.
$\example{1}$ Evaluate $\lim_{x\to 1} |x+5|$
$\solution$
In evaluating limits, we should always try to substitute the value for the function first before considering alternative solutions. Thus, in this case, substitute $x$ with 1,
\[\begin{align*} \lim_{x\to 1} |x+5| &= |1+5| \\ &= |6| \\ &= 6 \tagans \end{align*}\]Since we have arrived at a value, there is no reason for us to pursue alternative solutions. Hence, the limit of the function is 6.
$\example{2}$ Evaluate $\lim_{x\to 0} \frac{|x|}{x}$
$\solution$
In this example, if we directly substitute 0 into the expression, we would get $\frac{0}{0}$ which is undefined. Thus, in this case, we need to resort to a different approach.
The first method we’ll attempt is to substitute values approaching zero from both sides.
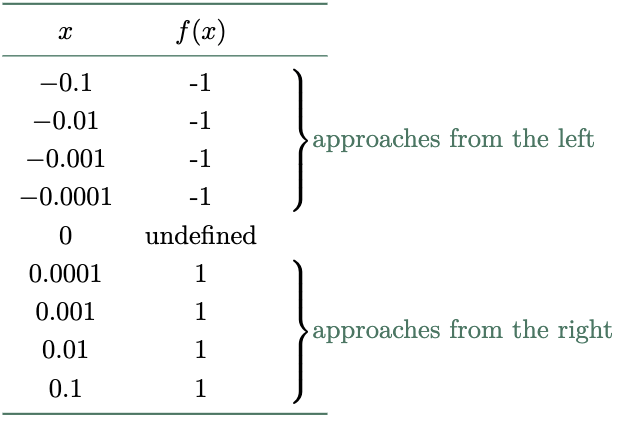
Thus, the left-hand limit is,
\[\lim_{x\to 0^-} \frac{|x|}{x} = -1\]And the right hand-limit is,
\[\lim_{x\to 0^+} \frac{|x|}{x} = 1\]Since the left and right hand limits do not approach the same value, the limit as $x$ approaches $0$ does not exist.
\[\begin{align*} \lim_{x\to 0^-} \frac{|x|}{x} &\neq \lim_{x\to 0^+} \frac{|x|}{x} \\ \lim_{x\to 0} \frac{|x|}{x} &= \mathrm{DNE} \tagans \end{align*}\]Another method, is by breaking down the absolute value,
\[|x|= \begin{cases} \tcB{x}, & \text{if $x \geq 0$ $\quad \tcAal{approaches from the right}$} \\ \tcB{-x}, & \text{if $x<0$ $\quad \tcAal{approaches from the left}$} \end{cases}\]As $x$ approaches to the right,
\[\begin{align*} \lim_{x\to 0^+} \frac{|x|}{x} &= \lim_{x\to 0^+} \frac{ \tcB{x} }{x} \\ &= 1 \end{align*}\]And, as $x$ approaches to the left,
\[\begin{align*} \lim_{x\to 0^-} \frac{|x|}{x} &= \lim_{x\to 0^-} \frac{ \tcB{-x} }{x} \\ &= -1 \end{align*}\]With this method, the result would be the same.
\[\begin{align*} \lim_{x\to 0^-} \frac{|x|}{x} &\neq \lim_{x\to 0^+} \frac{|x|}{x} \\ \lim_{x\to 0} \frac{|x|}{x} &= \mathrm{DNE} \tagans \end{align*}\]$\example{3}$ Evaluate $\lim_{x\to 3^+} \frac{|x-3|}{x-3}$
$\solution$
Break down the absolute value,
\[|x-3|= \begin{cases} \phantom{-}\tcB{(x-3)}, & \text{if $x > 3$ $\quad \tcAal{approaches from the right}$} \\ -(x-3), & \text{if $x<3$ $\quad \tcAal{approaches from the left}$} \end{cases}\]Since we are only required to determine the the right-hand limit,
\[\begin{align*} \lim_{x\to 3^+} \frac{|x-3|}{x-3} &= \lim_{x\to 3^+} \frac{\tcB{(x-3)}}{x-3} \\ &= 1 \tagans \end{align*}\]$\example{4}$ Evaluate $\lim_{x\to 7} \frac{|7-x|}{7-x}$
$\solution$
Break down the absolute value,
\[|7-x|= \begin{cases} \tcB{-(7-x)}, & \text{if $x > 7$ $\quad \tcAal{approaches from the right}$} \\ \phantom{-}\tcB{(7-x)}, & \text{if $x<7$ $\quad \tcAal{approaches from the left}$} \end{cases}\]As $x$ approaches to the right,
\[\begin{align*} \lim_{x\to 7^+} \frac{|7-x|}{7-x} &= \lim_{x\to 7^+} \frac{ \tcB{-(7-x)} }{7-x} \\ &= -1 \end{align*}\]And, as $x$ approaches to the left,
\[\begin{align*} \lim_{x\to 7^-} \frac{|7-x|}{7-x} &= \lim_{x\to 7^-} \frac{ \tcB{(7-x)} }{7-x} \\ &= 1 \end{align*}\]Since the left and right hand limits do not approach to the same value, the limit as $x$ approaches 7 does not exist.
\[\begin{align*} \lim_{x\to 7^-} \frac{|7-x|}{7-x} &\neq \lim_{x\to 7^+} \frac{|7-x|}{7-x} \\ \lim_{x\to 7} \frac{|7-x|}{7-x} &= \mathrm{DNE} \tagans \end{align*}\]$\example{5}$ Evaluate $\lim_{x\to -2^-} \frac{2x+4}{|x+2|}$
$\solution$
Factor the numerator,
\[\lim_{x\to -2^-} \frac{2x+4}{|x+2|} = \lim_{x\to -2^-} \frac{2(x+2)}{|x+2|}\]Then, break down the absolute value,
\[|x+2|= \begin{cases} \phantom{-}(x+2), & \text{if $x > -2$ $\quad \tcAal{approaches from the right}$} \\ \tcB{-(x+2)}, & \text{if $x<-2$ $\quad \tcAal{approaches from the left}$} \end{cases}\]Since we are only required to determine the left-hand limit,
\[\begin{align*} \lim_{x\to 2^-} \frac{2x+4}{|x+2|} &= \lim_{x\to 2^-} \frac{2(x+2)}{\tcB{-(x+2)}} \\ &= \frac{-2\cancel{(x+2)}}{\cancel{\tcB{(x+2)}}} \\ &= -2 \tagans \end{align*}\]
