An intuitive way to determine if a function is continuous, is if the graph of such function can be drawn without lifting up the pen, which emphasizes that there is no break on the curve. However, there are also instances that a graph cannot be easily sketched especially if the function is complicated. In such cases, continuity can be determined mathematically.
We can determine if the function is continuous if $\lim\limits_{x\to a}{f(x)}$ exists, $f(a)$ is defined, and $\lim\limits_{x\to a}{f(x)}=f(a)$, which tells us that the value of the function where $x=a$ is equal to the limit $f(a)=L$.
$$\begin{align} \lim\limits_{x\to a}{f(x)}=f(a) \end{align}$$
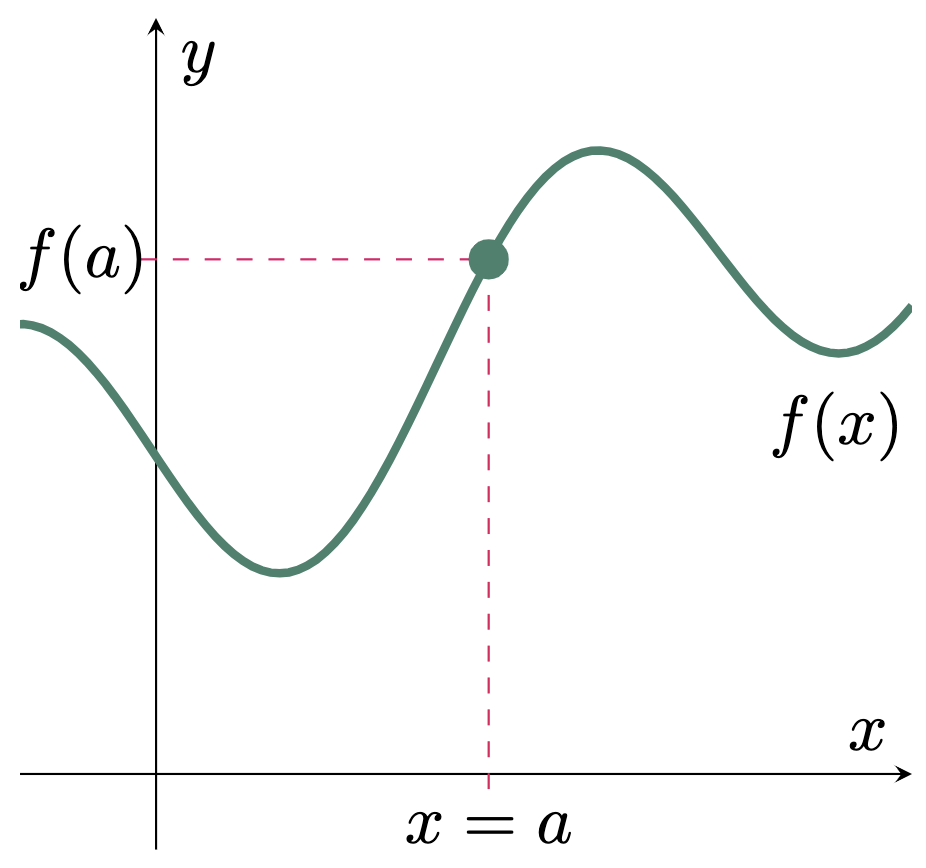
Figure 1: $\lim\limits_{x\to a}{f(x)}=f(a)$
Furthermore, since the limit must exist in order for a function to be continuous, the left-hand and right-hand limits of the function must be approaching to the same value. $\lim\limits_{x\to a^-}{f(x)}=\lim\limits_{x\to a^+}{f(x)}$. Otherwise, if the conditions are not satisfied, the function is said to be discontinuous.
Discontinuity
Consider the graph in Figure 2a, the curve has a hole at $x=a$ and $f(a)=1$ hence, $\lim\limits_{x\to a}{f(x)} \neq f(a)$ and thus, the function is discontinuous at $x=a$. In Figure 2b, the curve suddenly jumps at $x=a$ hence, $\lim\limits_{x\to a^-}{f(x)} \neq \lim\limits_{x\to a^+}{f(x)}$ and thus, the function is also discontinuous at $x=a$. And in Figure 2c, the curve has no hole nor did it jump and $\lim\limits_{x\to a}{f(x)}=f(a)$ hence, the function is continuous at $x=a$.
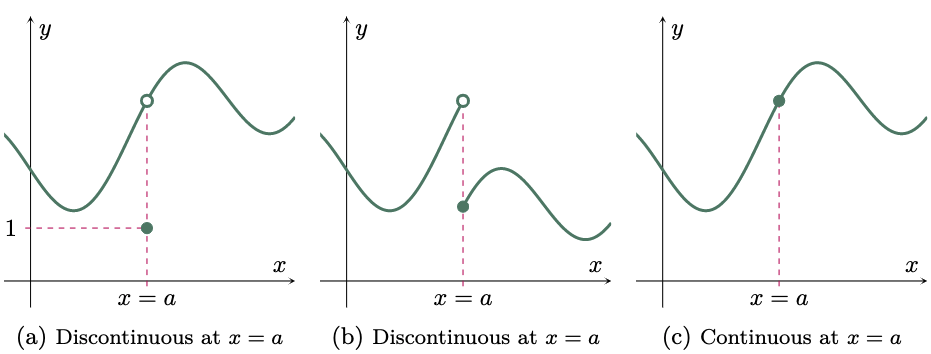
Figure 2: Continuity and Discontinuity
Types of Discontinuities
There are two types of discontinuities: Removable and Non-Removable Discontinuity. Think of if this way, if its removable “something is missing” and if its non-removable “it suddenly jumps”.
Consider the graph of a removable discontinuity (Figure 3a), we can easily make the function continuous by just plugging the hole at $x=a$. However, for the non-removable discontinuities, the left and right hand limits are approaching different values so, these type of discontinuities are much easier to visually distinguish from a continuous function (Figures 3b and 3c).
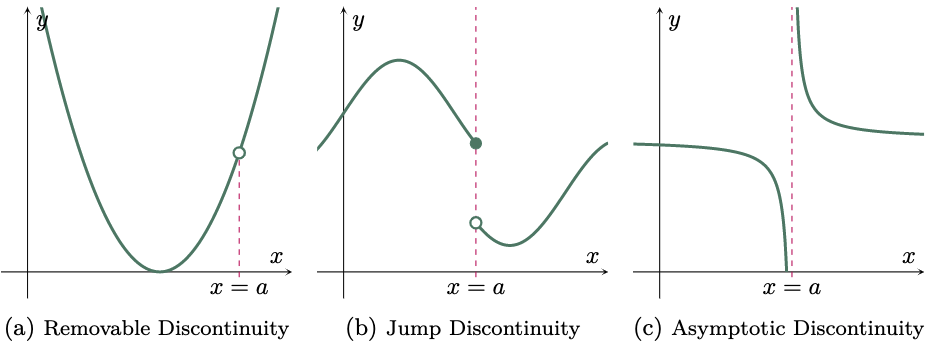
Figure 3: Types of discontinuities
$\typB{Removal Discontinuity}$
The curve in a removal discontinuity appears to be continuous except at the point where $x=a$ (Figure 3a). In this type of discontinuity, the limit still exists but $f(a)$ is either undefined or not equal to the limit.
$\typB{Jump Discontinuity (Non-Removal Discontinuity)}$
The curve in jump discontinuity (Figure 3b) is disconnected at the point $x=a$, these appears when the left and right hand limits are not equal to each other.
$\typB{Asymptotic Discontinuity (Non-Removal Discontinuity)}$
In asymptotic discontinuity, the curve approaches the line $x=a$ but does not meet with each other. Simply put, the line $x=a$ is the asymptote of the curve (Figure 3c). This type of discontinuity is sometimes called as Infinite Discontinuity since it occurs if the limit approaches to positive or negative infinity.
$\example{1}$ Determine if the function $f(x)=2x^{2}-1$ is continuous or not at $x=2$.
$\solution$
The function is continuous at $x=a$ if $\lim_{x\to a} f(x)=f(a)$.
For $\lim_{x\to a} f(x)$,
\[\begin{align*} \lim_{x\to 2} (2x^{2}-1) &= 2(2)^2-1 \\ &= 2(4)-1 \\ &= 7 \end{align*}\]And for $f(a)$,
\[\begin{align*} f(2) &= 2(2)^{2}-1 \\ &= 7 \end{align*}\]Since $\lim_{x\to 2} f(x)=f(2)$, the function is continuous.
$\example{2}$ Determine if the function $f(x)=\frac{4|x-5|}{x-5}$ is continuous or not at $x=5$.
$\solution$
Break down the absolute value,
\[|x-5|= \begin{cases} \phantom{-}\tcB{(x-5)}, & \text{if $x > 5$ $\quad \tcAal{approaches from the right}$} \\ \tcB{-(x-5)}, & \text{if $x<5$ $\quad \tcAal{approaches from the left}$} \end{cases}\]As $x$ approaches to the right,
\[\begin{align*} \lim_{x\to 5^+} \frac{4|x-5|}{x-5}&= \frac{4\tcB{(x-5)} }{x-5} \\ &= 4 \end{align*}\]And, as $x$ approaches to the left,
\[\begin{align*} \lim_{x\to 5^-} \frac{4|x-5|}{x-5} &= \frac{4[{\tcB{-(x-5)}}] }{x-5} \\ &= \frac{-4(x-5)}{x-5} \\ &= -4 \end{align*}\]Since the left and right hand limits do not approach to the same value, the limit as $x$ approaches 5 does not exist. Thus, the function is not continuous at $x=5$.
$\example{3}$ Find the point/s of discontinuity of the function $f(x)=\frac{x^2-16}{x-4}$
$\solution$
Discontinuities occur where the function is undefined. In this example, at $x=4$ both the numerator and the denominator becomes 0.
Hence, the function is discontinuous at $x=4$.
$\example{4}$ Find the point/s of discontinuity of the function $f(x)=\frac{2x}{x^2+x-6}$
$\solution$
Factor the denominator,
\[\begin{align*} \frac{2x}{x^2+x-6} &= \frac{2x}{(x+3)(x-2)} \end{align*}\]In this example, the denominator becomes 0 at $x=-3$ or $x=2$. And whenever the denominator is 0, the function is considered undefined.
Hence, the function is discontinuous at $x=-3$ and $x=2$.

