Introduction
In this lesson, we will try to establish the fundamental notions of derivatives. But before we begin, let us review some of the concepts necessary to adequately comprehend derivatives, as this concept distinguishes Differential Calculus from other branches of mathematics that you may have studied in your earlier years.
Increments
The increment of the variable indicates the change of the value of a variable. The increment is represented by the symbol $\Delta$ (delta), and is written before the variable to denote change. For example, if $x$ changes from $x_1$ to $x_2$, the increment of $x$ is equal to $x_2- x_1$.
$$\begin{align} \Delta x=x_2- x_1 \end{align}$$
The Derivative
To understand what a derivative is, let us start by recalling the slope of a line. A slope is commonly denoted by the symbol “$m$,” known simply as the “rise over run” or the “ratio of the difference of the $y$-coordinates and the difference of the $x$-coordinates between two specified positions” (see Figure 1). Furthermore, the slope of a line can be represented by any two points on the same plane, and the slope remains constant regardless of how far or close the points are separated, which is what defines it as a line.
$$\begin{align} m = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1} \end{align}$$
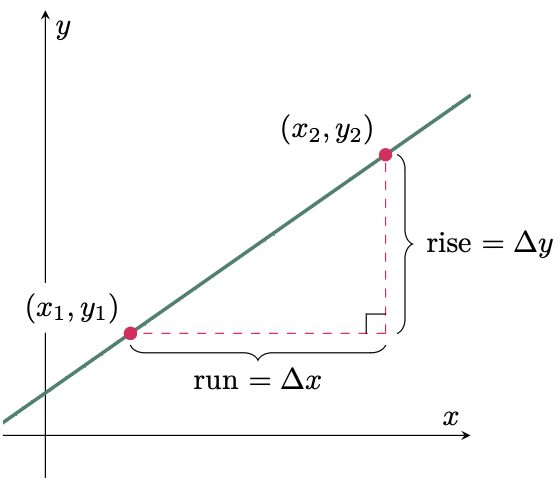
Figure 1: Slope of a line
However, if a graph does not represent a line (Figure 2a), getting the slope is not as easy as determining the slope of a line since its slope varies from one point to the other (Figure 2b). Nevertheless, what makes calculus so remarkable is that we can use the concept of limits to find the slope of the tangent line at any point on the curve.
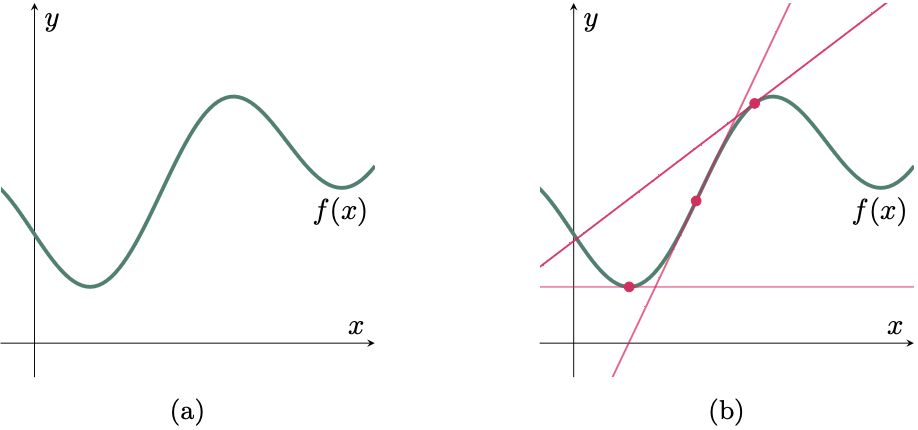
Figure 2: Slope of a curve
To determine the slope of a tangent line, we will start by locating two points on the curve, then connect these points with a line (Figure 3a). Bear in mind that our objective is to determine the slope at a single point. Therefore, let us bring the two points relatively close to each other (Figure 3b). And as the points get closer and closer to each other, the change in $x$ “$\Delta x$” approaches zero. Thus, $\lim_{\Dx\to 0} \frac{\Delta y}{\Delta x}$.
The slope of the tangent line is denoted as $\frac{dy}{dx}$, and this is what we call a derivative. Hence,
$$\begin{align} \frac{dy}{dx} = \lim_{\Dx\to 0} \frac{\Delta y}{\Delta x} \label{eq:the derivative 1} \end{align}$$
Which is read as the “derivative of $y$ with respect to $x$ is equal to the limit of the ratio of ${\Delta y}/{\Delta x}$ as $\Delta x$ approaches 0”.
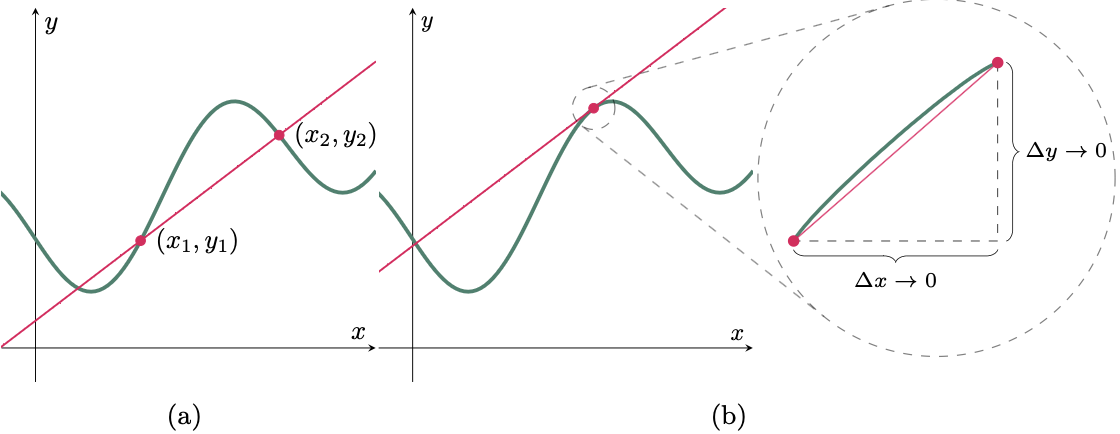
Figure 3: Slope of the tangent line of a curve
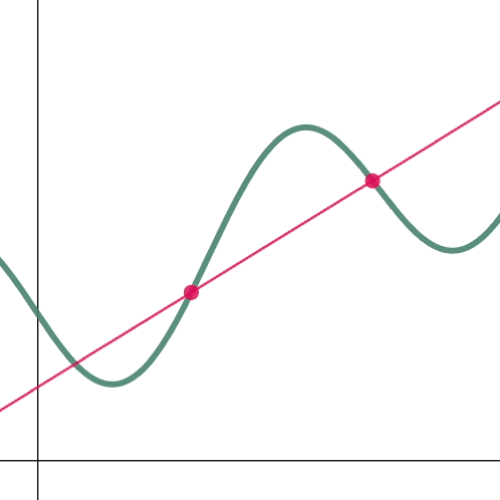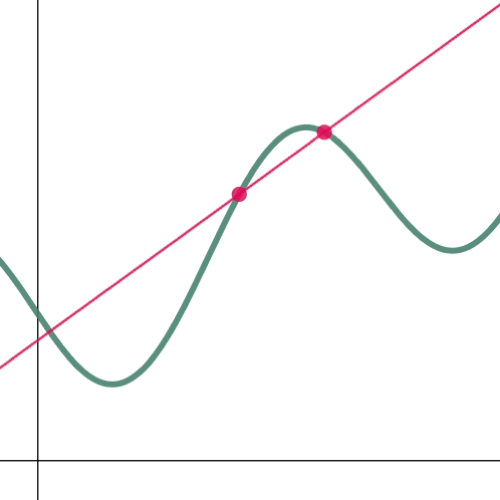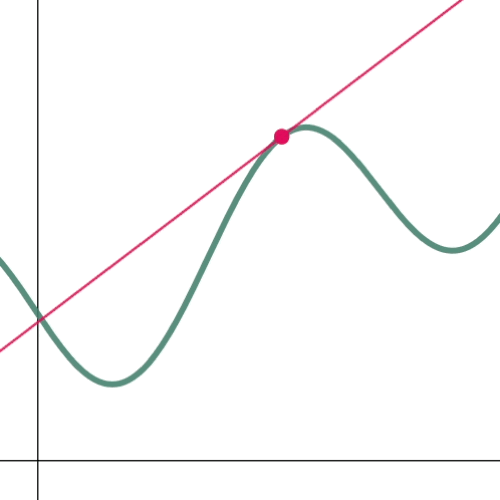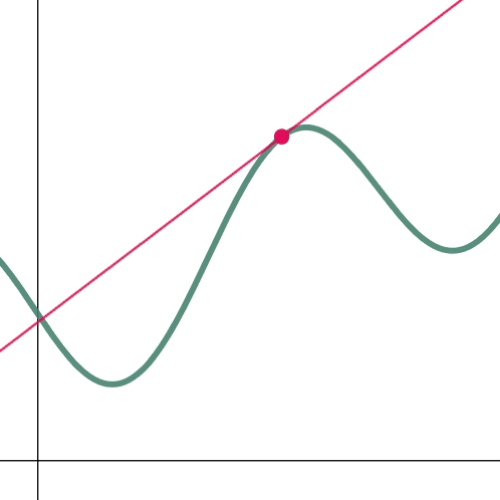
Figure 4: Approaching $\D{x}$ to zero (0)
Differentiation is the process of finding the derivative. And to evaluate the derivative of a function, consider the function,
\[\begin{align*} y &= f(x) \end{align*}\]Then add $\Delta x$ and $\Delta y$ to $x$ and $y$ respectively,
\[\begin{align*} y+\Delta y &= f(x+\Delta x) \\ \Delta y &= f(x+\Delta x)-y \end{align*}\]Since $y=f(x)$,
\[\begin{align*} \Delta y &= f(x+\Delta x)-f(x) \end{align*}\]Divide both sides by $\Delta x$,
\[\begin{align*} \frac{\Delta y}{\Delta x} &= \frac{f(x+\Delta x)-f(x)}{\Delta x} \end{align*}\]From $\eref{eq:the derivative 1}$,
\[\begin{align*} \frac{dy}{dx} &= \lim_{\Dx\to 0} \frac{\Delta y}{\Delta x} \\ &= \lim_{\Dx\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \\ \end{align*}\]Therefore, the derivative of $y$ with respect to $x$ is,
$$\begin{align} \frac{dy}{dx} = \lim_{\Dx\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \label{eq:the derivative delta notation} \end{align}$$
$\example{1}$ Differentiate the function $y=5x+2$
$\solution$
Add $\Delta x$ and $\Delta y$ to $x$ and $y$ respectively,
\[\begin{align*} % y+\Dy &= f(x+\Dx) \\ y+\Dy &= 5(x+\Dx)+2 \\ &= 5x+5\Dx+2 \\ \Dy &= 5x+5\Dx+2 -y \end{align*}\]Since $y=5x+2$,
\[\begin{align*} \Dy &= 5x+5\Dx+2 -(5x+2) \\ &= \cancel{5x}+5\Dx+\cancel{2} -\cancel{5x}-\cancel{2} \\ &= 5\Dx \end{align*}\]Divide both sides by $\Dx$,
\[\begin{align*} \frac{\Dy}{\Dx} &= \frac{5\cancel{\Dx} }{\cancel{\Dx}} \\ &= 5 \end{align*}\]Thus,
\[\begin{align*} \dydx &= \lim_{\Dx\to 0} 5 \\ &= 5 \tagans \end{align*}\]$\example{2}$ Differentiate the function $y=3-2x+x^2$
$\solution$
Add $\Delta x$ and $\Delta y$ to $x$ and $y$ respectively,
\[\begin{align*} y+\Dy &= 3-2(x+\Dx)+(x+\Dx)^2 \\ &= 3-2x-2\Dx+x^2+2x\Dx+\Dx^2 \\ \Dy &= 3-2x-2\Dx+x^2+2x\Dx+\Dx^2 -y \end{align*}\]Since $3-2x+x^2$,
\[\begin{align*} \Dy &= 3-2x-2\Dx+x^2+2x\Dx+\Dx^2 -(3-2x+x^2) \\ &= \cancel{3}-\cancel{2x}-2\Dx+\cancel{x^2}+2x\Dx+\Dx^2 - \cancel{3}+\cancel{2x}-\cancel{x^2} \\ &= -2\Dx+2x\Dx+\Dx^2 \end{align*}\]Divide both sides by $\Dx$,
\[\begin{align*} \frac{\Dy}{\Dx} &= \frac{\cancel{\Dx}(-2+2x+\Dx)}{\cancel{\Dx}} \\ &= -2+2x+\Dx \end{align*}\]Thus,
\[\begin{align*} \dydx &= \lim_{\Dx\to 0} (-2+2x+\Dx) \\ &= -2+2x+0 \\ &= 2x-2 \tagans \end{align*}\]$\example{3}$ Differentiate the function $x=\frac{1}{t^2}$
$\solution$
Add $\Delta x$ and $\Delta t$ to $x$ and $t$ respectively,
\[\begin{align*} x+\Dx &= \frac{1}{(t+\D t)^2} \\ \Dx &= \frac{1}{(t+\D t)^2} - \frac{1}{t^2} \\ &=\frac{(1)t^2-(1)(t+\D t)^2}{t^2(t+\D t)^2} \\ &=\frac{t^2-(t^2+2t\D t+\D t^2)}{t^2(t+\D t)^2} \\ &=\frac{-2t\D t-\D t^2}{t^2(t+\D t)^2} \end{align*}\]Divide both sides by $\D t$,
\[\begin{align*} \frac{\Dx}{\D t} &= \frac{\cancel{\D t} (-2t-\D t)}{t^2(t+\D t)^2} \cdot \frac{1}{\cancel{\D t}} \end{align*}\]Thus,
\[\begin{align*} \frac{dx}{dt} &= \lim_{\D t\to 0} \frac{-2t-\D t}{t^2(t+\D t)^2} \\ &= \frac{-2t-0}{t^2(t+0)^2} \\ &= \frac{-2t}{t^4} \\ &= -\frac{2}{t^3} \tagans \end{align*}\]$\example{4}$ Differentiate the function $x=\frac{y-2}{2y+5}$
$\solution$
Add $\Delta x$ and $\Delta y$ to $x$ and $y$ respectively,
\[\begin{align*} x+\Dx &= \frac{(y+\Dy)-2}{2(y+\Dy)+5} \\ \Dx &= \frac{y+\Dy-2}{2y+2\Dy+5} - \frac{y-2}{2y+5} \\ &=\frac{(y+\Dy-2)(2y+5)-(y-2)(2y+2\Dy+5)}{(2y+2\Dy+5)(2y+5)} \\ &=\frac{(2y^2+2y\Dy-4y+5y+5\Dy-10)-(2y^2+2y\Dy+5y-4y-4\Dy-10)}{(2y+2\Dy+5)(2y+5)} \\ &=\frac{5\Dy+4\Dy}{(2y+2\Dy+5)(2y+5)} \\ &=\frac{9\Dy}{(2y+2\Dy+5)(2y+5)} \end{align*}\]Divide both sides by $\D y$,
\[\begin{align*} &=\frac{9\cancel{\Dy}}{(2y+2\Dy+5)(2y+5)} \cdot \frac{1}{\cancel{\Dy}} \end{align*}\]Thus,
\[\begin{align*} \frac{dx}{dy} &= \lim_{\Dy\to 0} \frac{9}{(2y+2\Dy+5)(2y+5)} \\ &= \frac{9}{(2y+2(0)+5)(2y+5)} \\ &= \frac{9}{(2y+5)(2y+5)} \\ &= \frac{9}{(2y+5)^2} \tagans \end{align*}\]$\example{5}$ Find the value of the derivative: $\frac{dz}{dw}$ at $w=3$, if $z=\sqrt{1+w}$.
$\solution$
Add $\Delta z$ and $\Delta w$ to $z$ and $w$ respectively,
\[\begin{align*} z + \D z &= \sqrt{1+(w+\D w)} \\ \D z &= \sqrt{1+w+\D w} - \sqrt{1+w} \end{align*}\]To combine the terms, multiply both the numerator and the denominator by the conjugate,
\[\begin{align*} &= \br{ \sqrt{1+w+\D w} - \sqrt{1+w} } \cdot \frac{\sqrt{1+w+\D w} + \sqrt{1+w}}{\sqrt{1+w+\D w} + \sqrt{1+w}} \end{align*}\]If you can recall in algebra, multiplying an expression by its conjugate results to the square of the difference of the two terms $(a+b)(a-b)=a^2-b^2$,
\[\begin{align*} &= \frac{ \br{ \sqrt{1+w+\D w} }^2 - \br {\sqrt{1+w} }^2 }{\sqrt{1+w+\D w} + \sqrt{1+w}} \\ &= \frac{\cancel{1}+\cancel{w}+\D w-\cancel{1}-\cancel{w}}{\sqrt{1+w+\D w} + \sqrt{1+w}} \\ &= \frac{\D w}{\sqrt{1+w+\D w} + \sqrt{1+w}} \end{align*}\]Divide both sides by $\D w$,
\[\begin{align*} \frac{\D z}{\D w} &=\frac{\cancel{\D w}}{\sqrt{1+w+\D w} + \sqrt{1+w}} \cdot \frac{1}{\cancel{\D w}} \end{align*}\]Thus,
\[\begin{align*} \frac{dz}{dw} &= \lim_{\D w\to 0} \frac{1}{\sqrt{1+w+\D w} + \sqrt{1+w}} \\ &= \frac{1}{\sqrt{1+w+0} + \sqrt{1+w}} \\ &= \frac{1}{2\sqrt{1+w}} \end{align*}\]At $w=3$, substitute $w$ with 3,
\[\begin{align*} &= \frac{1}{2\sqrt{1+3}} \\ &= \frac{1}{4} \tagans \end{align*}\]
