From the previous lesson, we have defined derivatives as a slope of a curve. In this lesson, we will explore how we can apply the concept of derivatives to solve for the slope of a tangent line of a curve at a specific point. To start, let us first review some of the properties of the slope of a line.
The slope of a line measures the steepness and direction of the line. The larger the value of the slope, the steeper it becomes. And the sign of the numerical value of the slope indicates its direction.
If the sign is positive (+), the direction of the line slants upward to the right (Figure 1a), and if the sign is negative (−), the line slopes down to the right (Figure 1b).
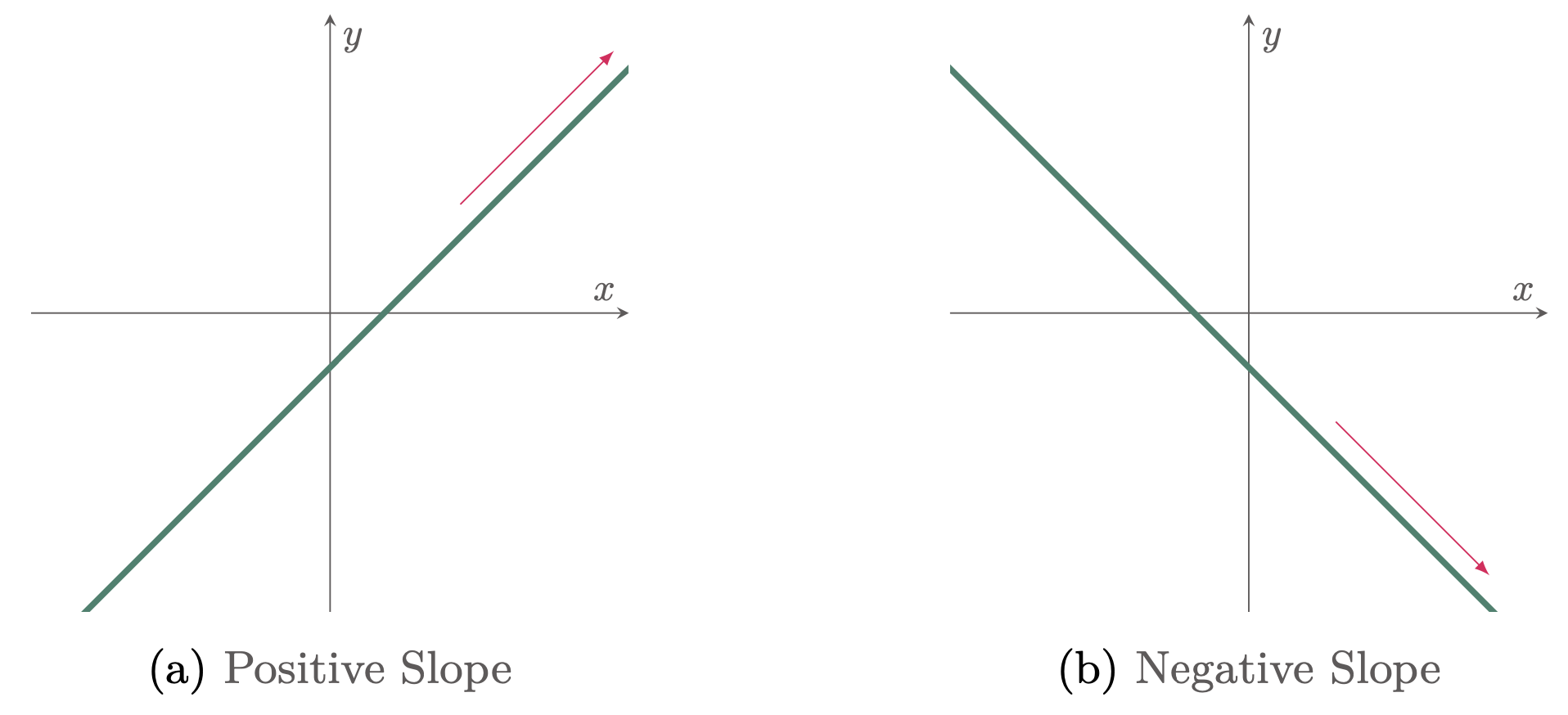
Figure 1: Direction of a curve
Slopes can also be equal to zero or undefined. A zero slope with a zero numerator indicates no change in the y-coordinates between any two points on the line, hence forming a horizontal line (Figure 2a). And an undefined slope has a zero denominator since any value divided to zero is undefined, indicating no change in the x-coordinates between any two points on the line, forming a vertical line (Figure 2b).
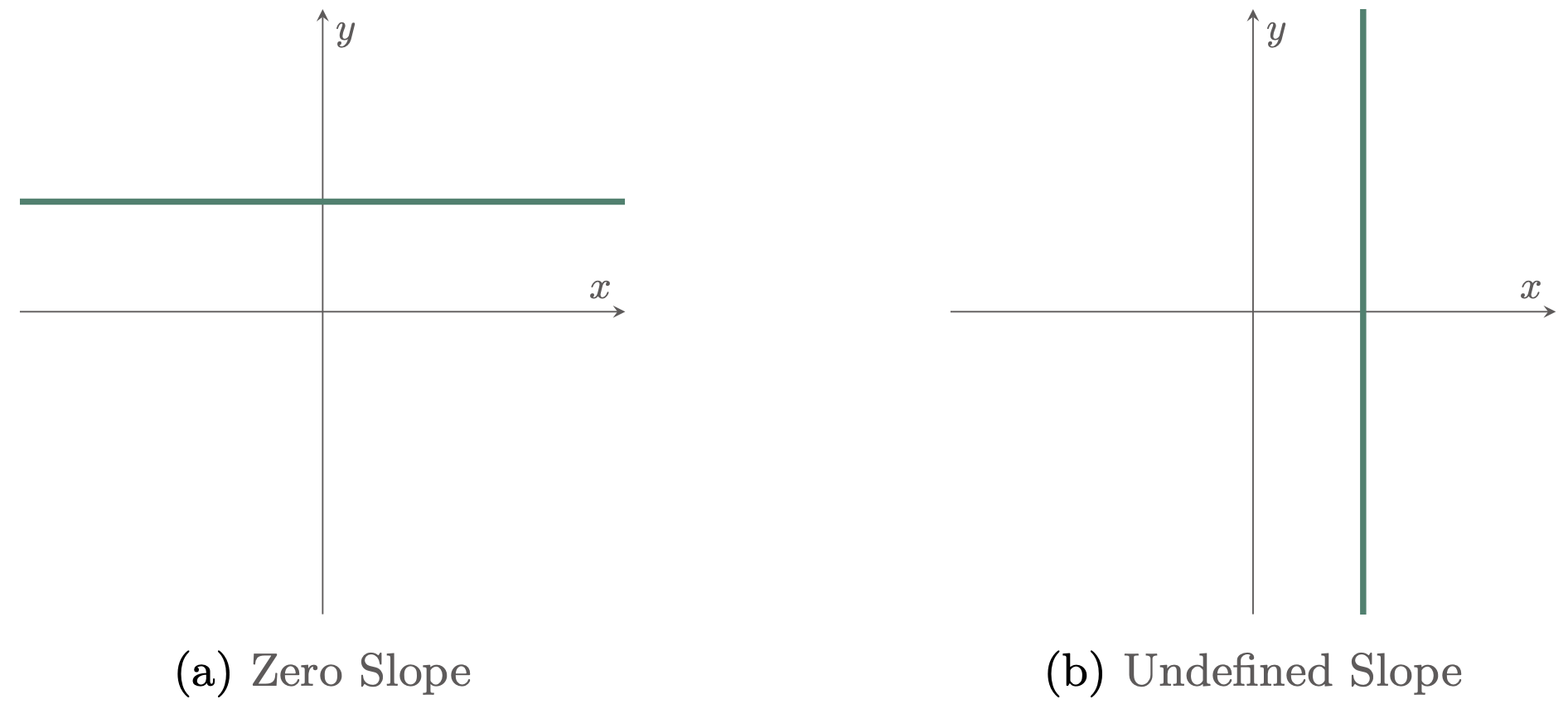
Figure 2: Horizontal and vertical lines
In solving for the slope of a curve, the first step that we need to undergo is to solve for the derivative of the equation of the curve.
dydx=lim
\example{1} Determine the slope of the line y=2x-3.
\solution
Differentiate y with respect to x,
\begin{align*} y+\Dy &= 2(x+\Dx)-3 \\ \Dy &= 2(x+\Dx)-3 - (2x-3) \\ &= \cancel{2x}+2\Dx-\cancel{3} - (\cancel{2x}-\cancel{3}) \\ &= 2\Dx \end{align*}Divide both sides by \Dx,
\begin{align*} \frac{\Dy}{\Dx} &= \frac{2\cancel{\Dx}}{\cancel{\Dx}} \end{align*}Thus,
\begin{align*} \frac{dy}{dx} &= \lim_{\Dx\to 0} 2 \\ &= 2 \tagans \end{align*}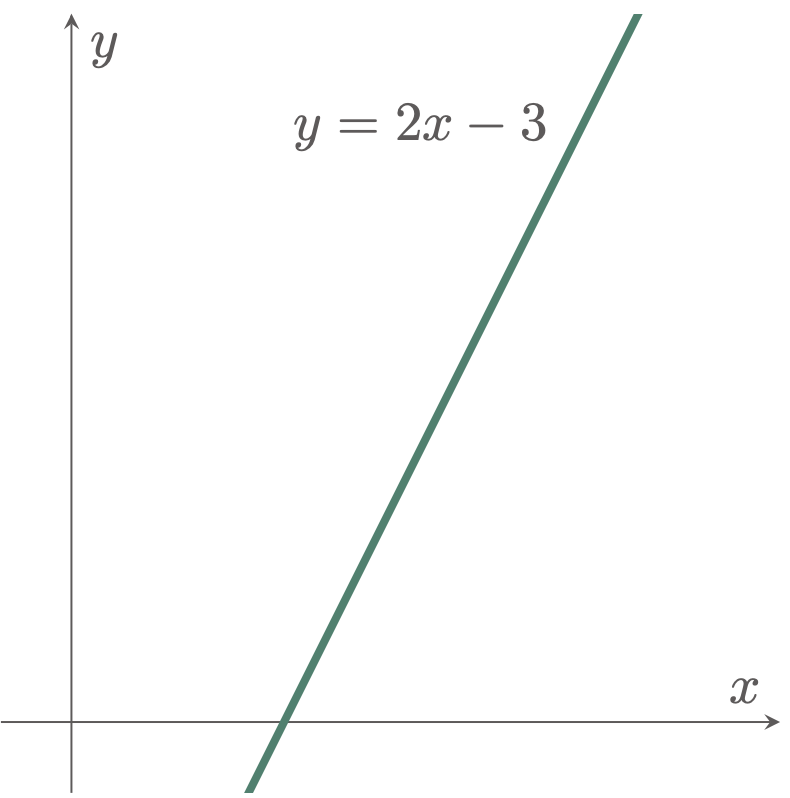
Since the function represents a line, the slope remains constant which is equal to 2 anywhere on the curve.
\example{2} Determine the slope of the curve y=3x^2+5x-2 at (-2,0).
\solution
Differentiate y with respect to x,
\begin{align*} y+\Dy &= 3(x+\Dx)^2+5(x+\Dx)-2 \\ \Dy &= 3(x^2+2x\Dx+\Dx^2)+5x+5\Dx-2 - (3x^2+5x-2) \\ &= \cancel{3x^2}+6x\Dx+3\Dx^2+\cancel{5x}+5\Dx-\cancel{2} - (\cancel{3x^2}+\cancel{5x}-\cancel{2}) \\ &= 6x\Dx+3\Dx^2+5\Dx \\ \frac{\Dy}{\Dx} &= \frac{\cancel{\Dx}(6x+3\Dx+5) }{\cancel{\Dx}} \end{align*}Thus,
\begin{align*} \frac{dy}{dx} &= \lim_{\Dx\to 0} 6x+3\Dx+5 \\ &= 6x+5 \end{align*}To determine the slope at point (-2,0), replace x with -2.
\begin{align*} \frac{dy}{dx} &= 6(-2)+5 \\ &= -7 \tagans \end{align*}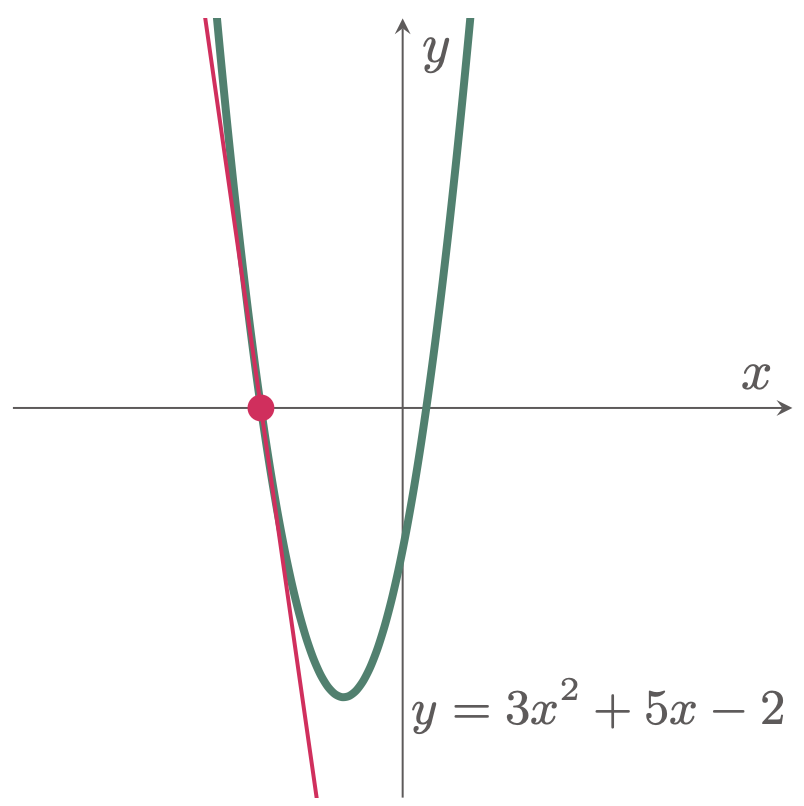
\example{3} Find y’(-1) of the curve y=\frac{3}{x^2+2}
\solution
Differentiate y with respect to x,
\begin{align*} y+\Dy &= \frac{3}{(x+\Dx)^2+2} \\ \Dy &= \frac{3}{(x+\Dx)^2+2}- \frac{3}{x^2+2} \\ &= \frac{ 3(x^2+2) - 3[x+\Dx)^2+2] }{ [(x+\Dx)^2+2](x^2+2) } \\ &= \frac{ \cancel{3x^2}+\cancel{6} - [\cancel{3x^2}+6x\Dx+3\Dx^2+\cancel{6}] }{ [(x+\Dx)^2+2](x^2+2) } \\ &= \frac{-6x\Dx-3\Dx^2}{ [(x+\Dx)^2+2](x^2+2) } \\ \frac{\Dy}{\Dx} &= \frac{\cancel{\Dx}(-6x-3\Dx)}{ [(x+\Dx)^2+2](x^2+2) } \cdot \frac{1}{\cancel{\Dx}} \end{align*}Thus,
\begin{align*} y' &= \lim_{\Dx\to 0} \frac{-6x-3\Dx}{ [(x+\Dx)^2+2](x^2+2) } \\ &= \frac{-6x}{ (x^2+2)(x^2+2) } \\ &= \frac{-6x}{(x^2+2)^2} \end{align*}At x=-1,
\begin{align*} y'(-1) &= \frac{-6(-1)}{[(-1)^2+2]^2} \\ % &= \frac{-6}{9} \\ &= \frac{2}{3} \tagans \end{align*}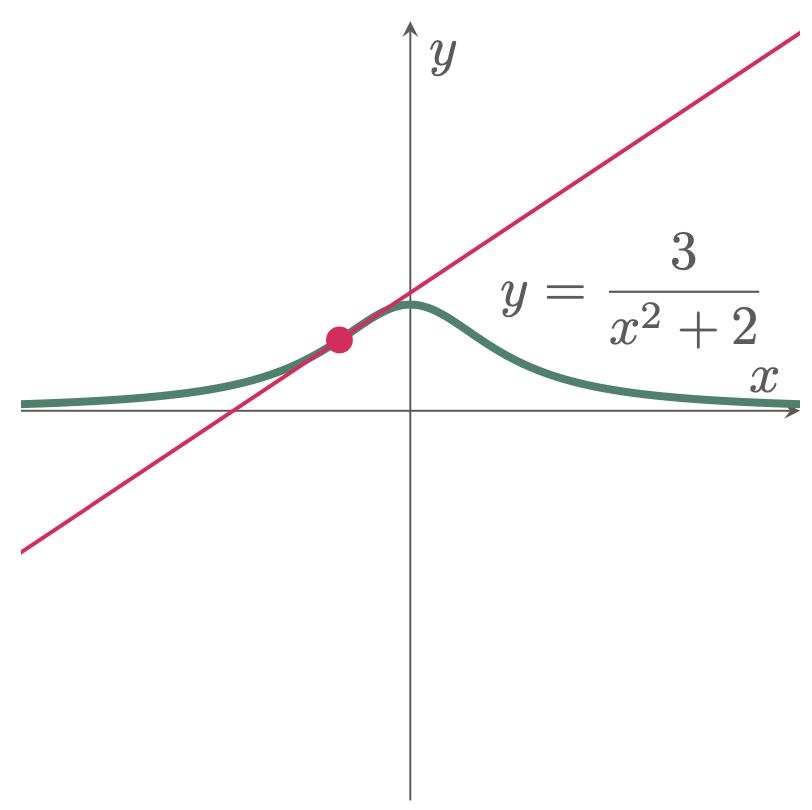
\example{4} Determine the slope of the curve y^2=2x+7 at y=3.
\solution
Differentiate y with respect to x,
\begin{align*} (y+\Dy)^2 &= 2(x+\Dx)+7 \\ y^2+2y\Dy+\Dy^2-7 &= 2(x+\Dx) \\ \frac12(y^2+2y\Dy+\Dy^2-7) &= \frac{\cancel{2}(x+\Dx)}{\cancel{2}} \\ x+\Dx &= \frac{1}{2} (y^2+2y\Dy+\Dy^2-7) \\ \Dx &= \frac{1}{2} (y^2+2y\Dy+\Dy^2-7) - x \end{align*}Since y^2=2x+7, x=\frac{1}{2} (y^2-7),
\begin{align*} \Dx &= \frac{1}{2} (\cancel{y^2}+2y\Dy+\Dy^2-\cancel{7}) - \frac{1}{2} (\cancel{y^2}-\cancel{7}) \\ &= \frac{2y\Dy+\Dy^2}{2} \end{align*}Divide both sides by \Dy,
\begin{align*} \frac{\Dx}{\Dy} &= \frac{\cancel{\Dy}(2y+\Dy)}{2} \cdot \frac{1}{\cancel{\Dy}} \end{align*}Thus,
\begin{align*} \frac{dx}{dy} &= \lim_{\Dy\to 0} \frac{2y+\Dy}{2} \\ &= \frac{\cancel{2}y}{\cancel{2}} \\ \frac{dx}{dy} &= y \end{align*}To get the derivative of y with respect to x, take the reciprocal of both sides,
\begin{align*} \frac{dy}{dx} &= \frac{1}{y} \end{align*}At y=3,
\begin{align*} &= \frac{1}{3} \tagans \end{align*}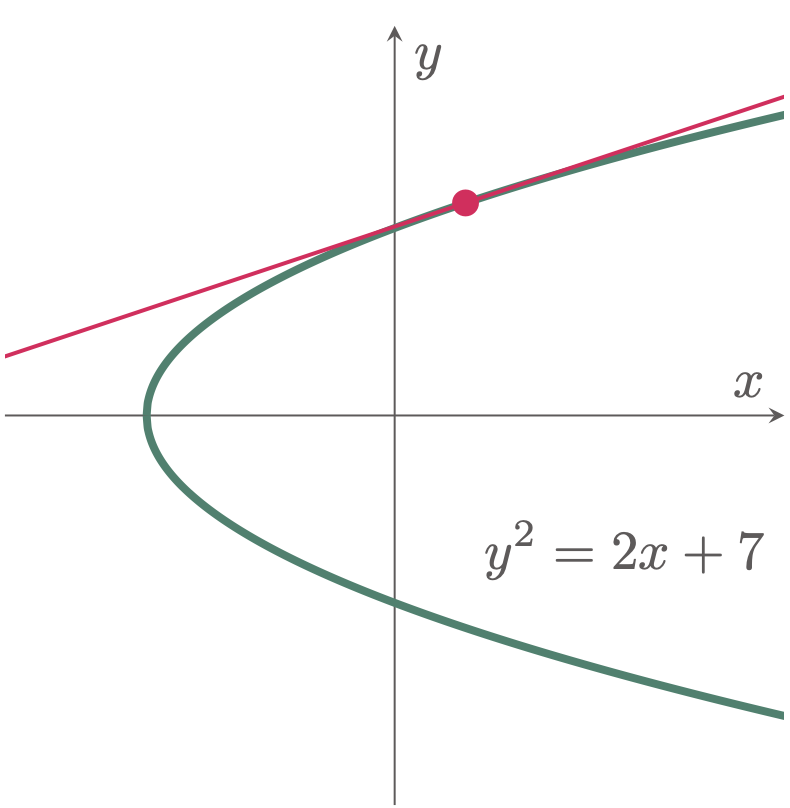
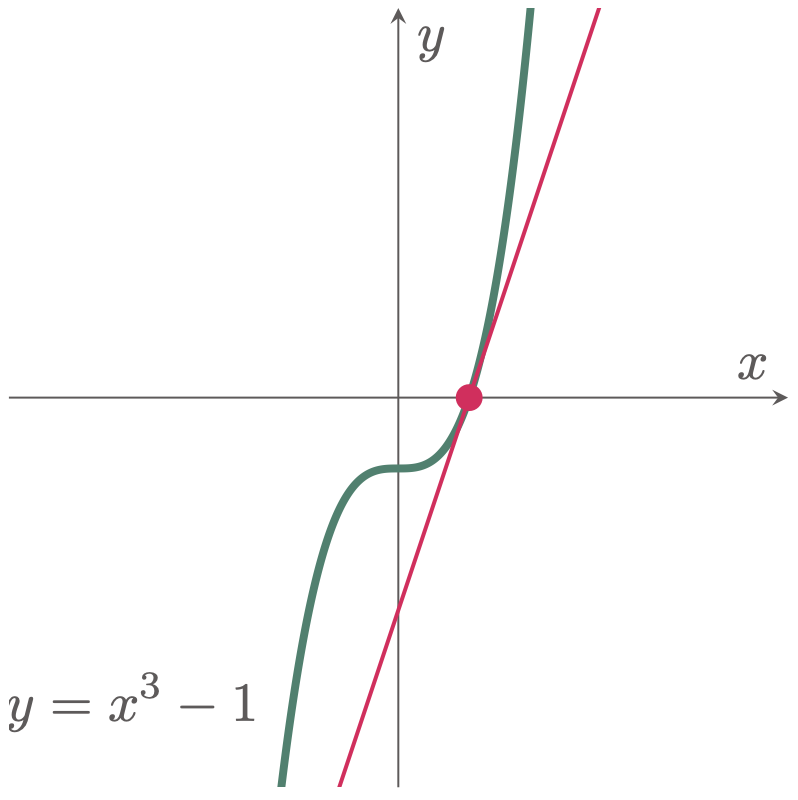
\example{5} Determine the slope of the curve y=x^3-1 where the curve intersects the x-axis.
\solution
Differentiate y with respect to x,
\begin{align*} y+\Dy &= (x+\Dx)^3-1 \\ \Dy &= \cancel{x^3}+3x^2\Dx+3x\Dx^2+\Dx^3-\cancel{1} - (\cancel{x^3}-\cancel{1}) \\ \frac{\Dy}{\Dx} &= \frac{\cancel{\Dx}(3x^2+3x\Dx+\Dx^2)}{\cancel{\Dx}} \\ \dydx &= \lim_{\Dx\to 0} (3x^2+3x\Dx+\Dx^2) \\ &= 3x^2 \end{align*}At the point where the curve intersects the x-axis, the y-coordinate is 0, y=0. Hence, solving for x using the given eqiation y=x^3-1 gives us,
\begin{align*} 0 &= x^3-1 \\ x &= 1 \end{align*}Hence, at point where x=1,
\begin{align*} \dydx &= 3(1)^2 \\ &= 3 \tagans \end{align*}