The rate of change indicates how fast a variable is changing with respect to another variable. For example, “How fast is the volume changing with respect to its radius?’’ or “how fast is the position of an object changing with respect to time?’’. But remember that this is also what a derivative intends to measure. So, the Rate of Change is an application of derivatives. And to understand this more clearly, let’s have some examples.
$\example{1}$ Find the rate of change of an area of a square with respect to its side.
$\solution$
We have already learned how to explicitly express one variable as a function of another in our lesson in Functions. In this example, before we can differentiate to find the rate of change, we must first represent the area of the square as a function of the length of its side.
\[\begin{align*} \text{Let: } A &= \text{area of the square} &\\ x &= \text{length of the side of the square} \end{align*}\]Hence, the equation for the area of a square is,
\[\begin{align*} A &= x^2 \end{align*}\]Then, differentiate $A$ with respect to $x$,
\[\begin{align*} A+\D{A} &= (x+\Dx)^2 \\ \D{A} &= \cancel{x^2}+2x\Dx+\Dx^2 - (\cancel{x^2}) \\ \frac{\D{A}}{\Dx} &= \frac{\cancel{\Dx}(2x+\Dx)}{\cancel{\Dx}} \\ \frac{dA}{dx} &= 2x \tagans \end{align*}\]Therefore, the rate of change of the area of the square with respect to its side is equal to twice the length of its side.
$\example{2}$ A spherical balloon has a volume of $V=\frac{4}{3}\pi r^3$. Determine how fast its volume is increasing with respect to its radius in $(\mathrm{in^3/in})$ when $r=5\un{in}$.
$\solution$
To determine the rate of change of the volume $V$ with respect to the radius $r$, differentiate $V$ with respect to $r$,
\[\begin{align*} V+\D{V} &= \frac{4}{3}\pi(r+\D{r})^3 \\ \D{V} &= \frac{4}{3}\pi(r^3+3r^2\D{r}+3r\D{r}^2+\D{r}^3) - \frac{4}{3}\pi r^3 \\ &= \cancel{\frac{4}{3}\pi r^3} +4\pi r^2\D{r}+4\pi r\D{r}^2+\frac{4}{3}\pi\D{r}^3 - \cancel{\frac{4}{3}\pi r^3} \\ \frac{\D V}{\D r} &= \frac{\cancel{\D r}(4\pi r^2+4\pi r\D{r}+\frac{4}{3}\pi\D{r}^2)}{\cancel{\D r}} \\ \frac{dV}{dr} &= \lim_{\D r\to 0} (4\pi r^2+4\pi r\D{r}+\frac{4}{3}\pi\D{r}^2) \\ &= 4\pi r^2 \end{align*}\]At $r=5\un{in}$,
\[\begin{align*} &= 4\pi (5\un{in})^2 \\ \frac{dV}{dr} &= 100\pi\un{in^2} \qquad{\text{or}}\qquad 100\pi\un{in^3/in} \tagans \end{align*}\]$\example{3}$ A right circular cone’s radius increases as its height remains constant ($h=10\un{cm}$). Find the rate of change of the cone’s volume with respect to its radius.
$\solution$
\[\begin{align*} \text{Let: } V &= \text{volume of the cone} \hspace{100cm} \\ r &= \text{radius of the base oh the cone} \\ h &= \text{height of the cone} \end{align*}\]
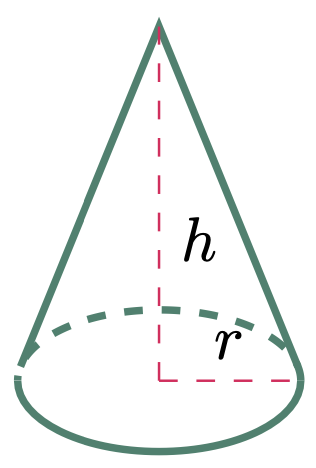
Hence, the equation for the volume of a cone is,
\[\begin{align*} V &= \frac{1}{3}\pi r^2 h \end{align*}\]Then, differentiate $V$ with respect to $r$,
\[\begin{align*} V+\D{V} &= \frac{1}{3}\pi (r+\D{r})^2 h \\ \D{V} &= \frac{1}{3}\pi (r^2+2r\D{r}+\D{r}^2) h - \frac{1}{3}\pi r^2 h \\ &= \cancel{\frac{1}{3}\pi r^2 h} + \frac{2}{3}\pi r\D{r}h+\frac{1}{3}\pi\D{r}^2 h - \cancel{\frac{1}{3}\pi r^2 h} \\ &= \frac{2}{3}\pi r\D{r}h+\frac{1}{3}\pi\D{r}^2 h \\ \frac{\D V}{\D r} &= \cancel{\D r}\br{ \frac{2}{3}\pi rh+\frac{1}{3}\pi\D{r} h } \cdot \frac{1}{\cancel{\D r}} \\ \frac{dV}{dr} &= \lim_{\D r\to 0} \br{ \frac{2}{3}\pi rh+\frac{1}{3}\pi\D{r} h } \\ &= \frac{2}{3}\pi rh \end{align*}\]Since $h=10\un{cm}$,
\[\begin{align*} &= \frac{2}{3}\pi r (10) \\ \frac{dV}{dr} &= \frac{20}{3}\pi r \un{cm^3/cm} \tagans \end{align*}\]
