From the previous chapters, we have already learned how to graph functions and have a strong understanding of how the slope of a curve works. Therefore, in this section, we will use the concepts we have previously learned to solve for the tangent and normal lines of a curve.
In our lesson in the “introduction to derivatives” and the “slope of a curve,” we have well established how the derivative is related to the slope of a tangent line on the curve. In this section, we will use the slope to define and compose an equation for both the tangent and normal lines of a curve. To start, let us first understand what tangent and normal lines are.
Tangent to a Curve
A tangent of a curve is a line that touches the curve at one point where its slope is the same as the slope of the curve at a specific point. The point where the line and the curve intersects is what we call the point of tangency.
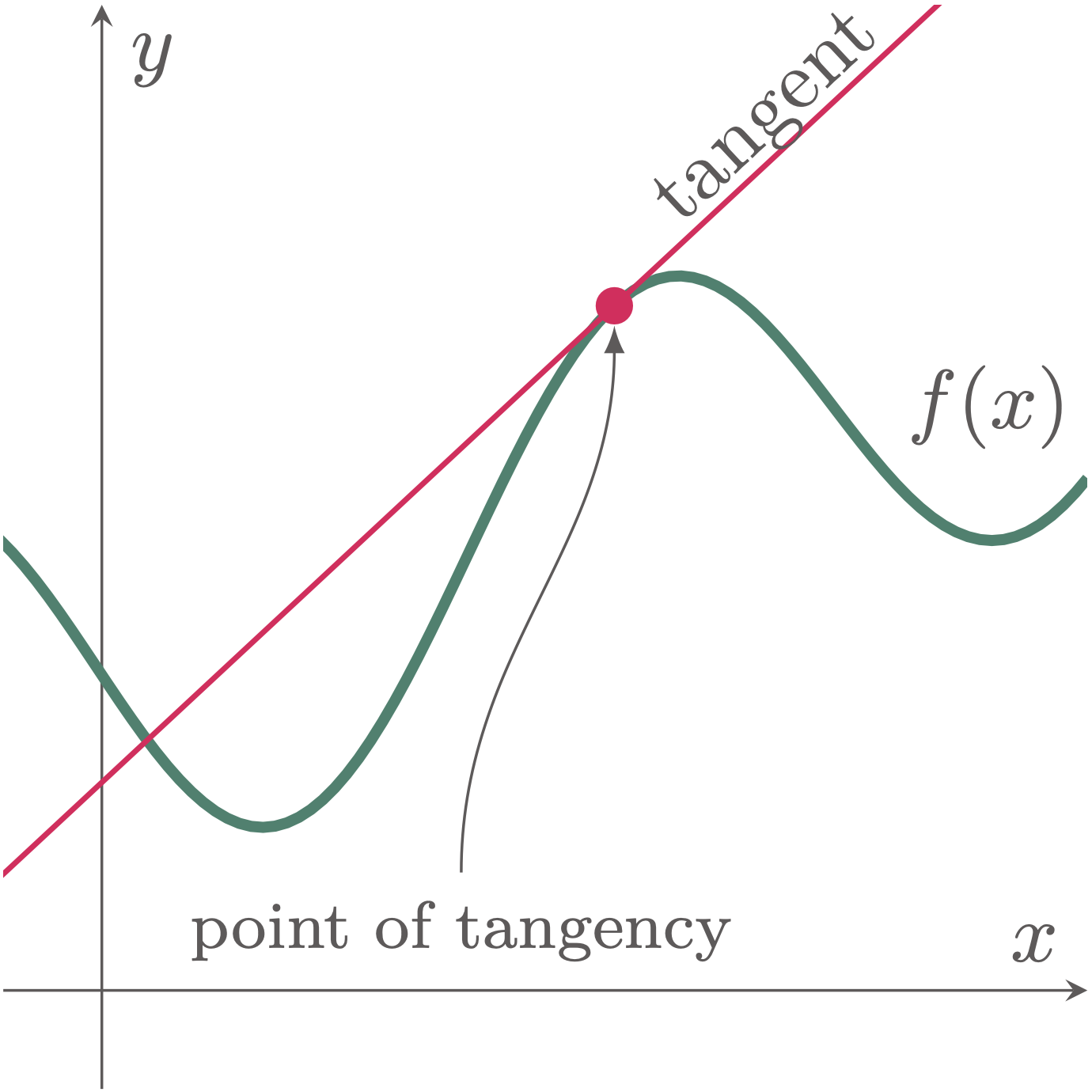
Figure 1: A point of tangency is the intersection of a curve and its tangent line at a point where both have equal slopes
If you are wondering in $\fref{2}$, how about the other point intersecting the curve at Point $B$?. Since the slope of the line and the curve at Point $B$ does not match, we cannot call it a point of tangency; it is merely an intersection point between the line and the curve.
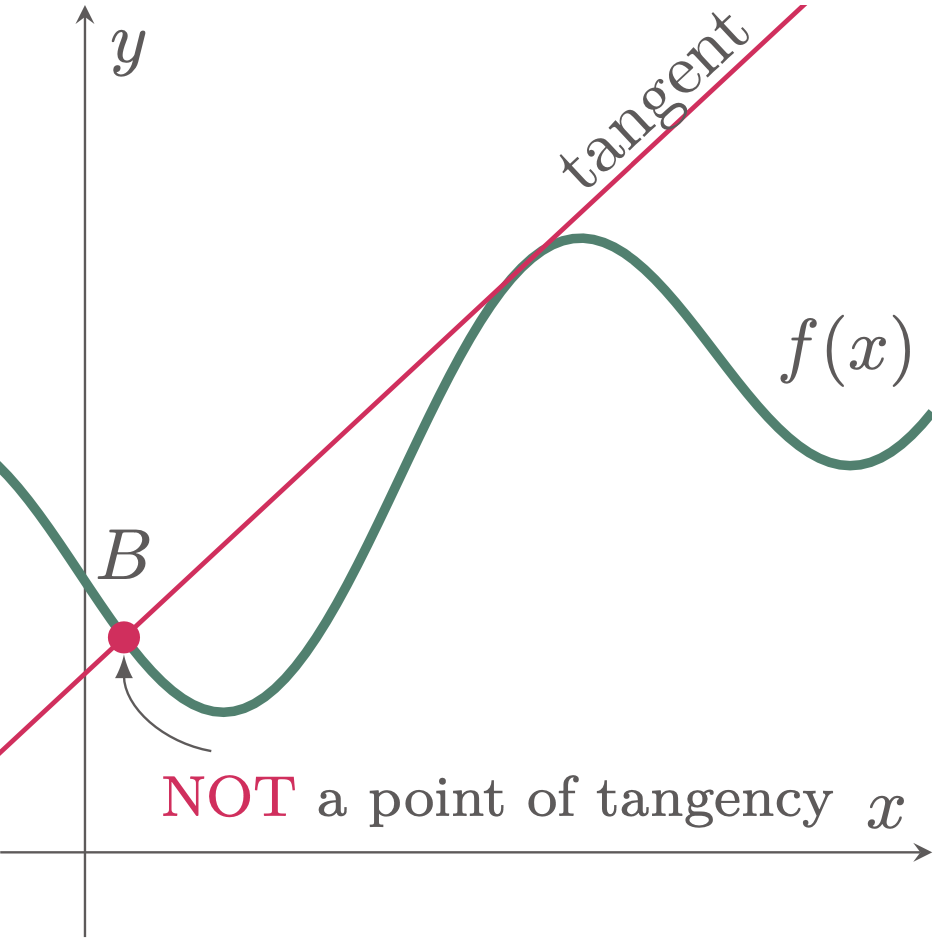
Figure 2: The point at which a line intersects with a curve with unequal slopes is not considered a point of tangency.
Furthermore, a line tangent to a curve changes from one point to another, following the path of the curve. With this in mind, if we are to find the equation of a tangent line, we must first indicate where exactly it is located on the curve since tangent lines of the same curve vary from one location to another.
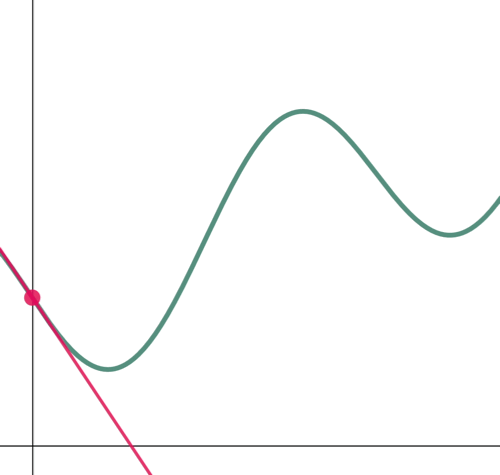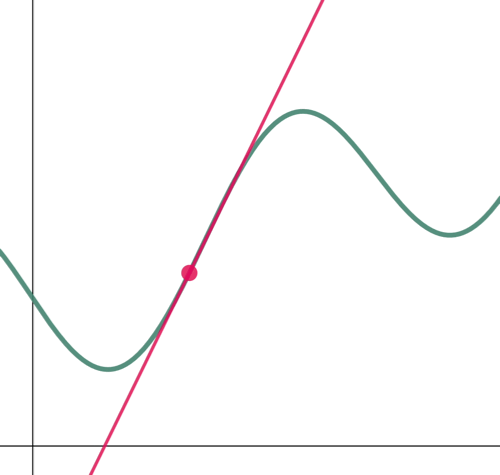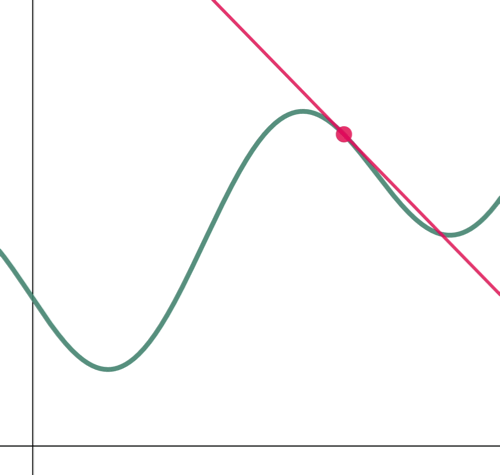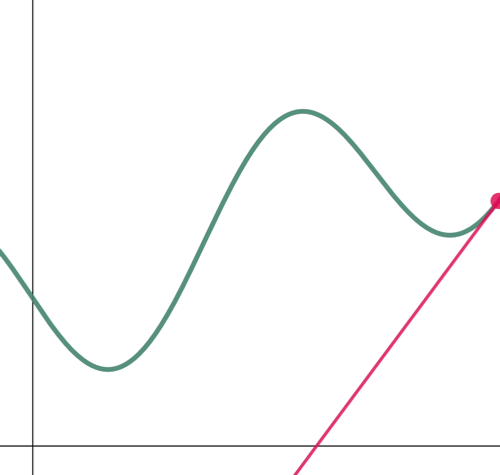
Figure 3: A tangent of a curve changes from one location to another.
Normal to a Curve
A line normal to a curve, on the other hand, is dependent on the tangent line. It is simply the line perpendicular to the tangent line. With this in mind, if we have already determined the slope of the tangent, we could easily solve for the slope of the normal line.
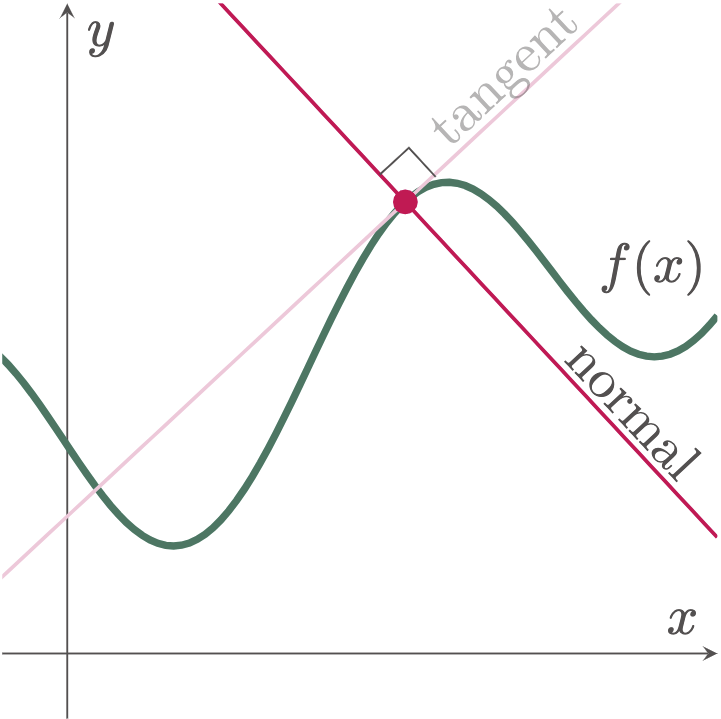
Figure 4: Normal to a curve is the line perpendicular to the tangent line.
If you could recall in Analytic Geometry, the slope of a perpendicular line is the negative reciprocal of the slope. Thus,
$$\begin{align} m_N = -\frac{1}{m_T} \label{eq:slope of normal line} \end{align}$$
Where $m_T$ denotes the slope of the tangent line, and $m_N$ as the slope of the normal line.

