From the previous section, we have learned how we can determine the slope of either a tangent or a normal line through differentiation, or in the case of normal lines, it can be easily determined by getting the negative reciprocal of the slope of the tangent line. In this section, we will learn how to utilize their slopes to find the general equation of such lines.
In determining the equation of a line, there are different methods available. However in our case, since we can easily determine the slope of the line by differentiation and the coordinates of a point on the line will most likely be available, we can specifically use the Point-Slope Form (\(\eref{eq:pt-slope of a line}\)) .
$$\begin{align} y-y_1=m(x-x_1) \label{eq:pt-slope of a line} \end{align}$$
Point-slope Form, by the name suggests, can be used to determine the equation of a line by using two parameters, namely: a point, and a slope of a line. To understand more how we can use this form, it is best to solve some problems.
$\example{1}$ Find the equation of the tangent and normal lines to the curve $y=x^3+3x^2+1$ at point $(1,5)$.
$\solution$
To get the slope of the tangent, differentiate the function with respect to $x$,
\[\begin{align*} \ddx\br{y} &= \ddx\br{x^3+3x^2+1} \\ \dydx &= 3x^2+6x \\ \end{align*}\]Then to find the slope of the tangent line at point $(1,5)$, replace the independent variable $x$ with 1.
\[\begin{align*} y-y_1 &= m_T (x-x_1) \\ m_T &= \dydx = 3(1)^2+6(1) \\ &= 9 \end{align*}\]Thus, the equation of the tangent line at point $(1,5)$ with a slope of 9 can be determined by using the Poin-Slope Form ($\eref{eq:pt-slope of a line}$)
\[\begin{align*} y-(5) &= 9[x-(1)] \\ y-5 &= 9x -9 \\ 9x-y &= 4 \tagans \end{align*}\]And for the slope of the normal line, get the negative reciprocal of the slope of the tangent,
\[\begin{align*} m_N &= -\frac{1}{m_T} \\ &= -\frac{1}{9} \end{align*}\]Hence, the equation of the normal line at point $(1,5)$ with a slope of $-\frac{1}{9}$ is,
\[\begin{align*} y-y_1 &= m_N (x-x_1) \\ y-(5) &= -\frac{1}{9}[x-(1)] \\ 9y-45 &= -x+1 \\ x+9y &= 46 \tagans \end{align*}\]Therefore, the equation of the tangent and normal lines are $9x-y = 4$ and $x+9y = 46$ respectively.
$\example{2}$ Find the equation of the tangent and normal lines to the curve $x^2+y^2+6x-8y=0$ at the origin.
$\solution$
In this example, since we are given an implicit function, the first step that we need to do is differentiate the given equation through Implicit Differentiation.
\[\begin{align*} \ddx\br{x^2+y^2+6x-8y} &= \ddx\br{0} \\ 2x+2y y' + 6 - 8 y' &= 0 \\ (2y-8) y' &= -2x-6 \\ y' &= \frac{-2x-6}{2y-8} \\ &= \frac{-x-3}{y-4} \end{align*}\]To determine the slope of the tangent line at the origin, which has a coordinates of $(0,0)$, substitute the variables of the derivative with the respective values of the coordinates.
\[\begin{align*} m_T &= y' = \frac{-0-3}{0-4} \\ &= \frac34 \end{align*}\]Solving for the equation of the tangent line using the Point-Slope Form ($\eref{eq:pt-slope of a line}$) gives us,
\[\begin{align*} y-y_1 &= m_T (x-x_1) \\ y-0 &= \frac34[x-0] \\ y &= \frac34x \\ 4y &= 3x \\ 4y-3x &= 0 \tagans \end{align*}\]Then for the equation of the normal line, we can directly plug the slope to the Point-Slope Form,
\[\begin{align*} y-y_1 &= m_N (x-x_1) \\ y-y_1 &= -\frac{1}{m_T} (x-x_1) \\ y-0 &= -\frac43 (x-0) \\ 3y &= -4x \\ 4x+3y &= 0 \tagans \end{align*}\]$\example{3}$ Find the equation of the tangent and normal lines to the curve $y=(x+4)^2$ at the point where the curve intersects the $y$-axis.
$\solution$
In this example, the coordinates of the point are not given. However, it is stated that the point is located where the curve intersects the $y$-axis. Thus, graphing the curve can give us a clearer picture of where it is located.
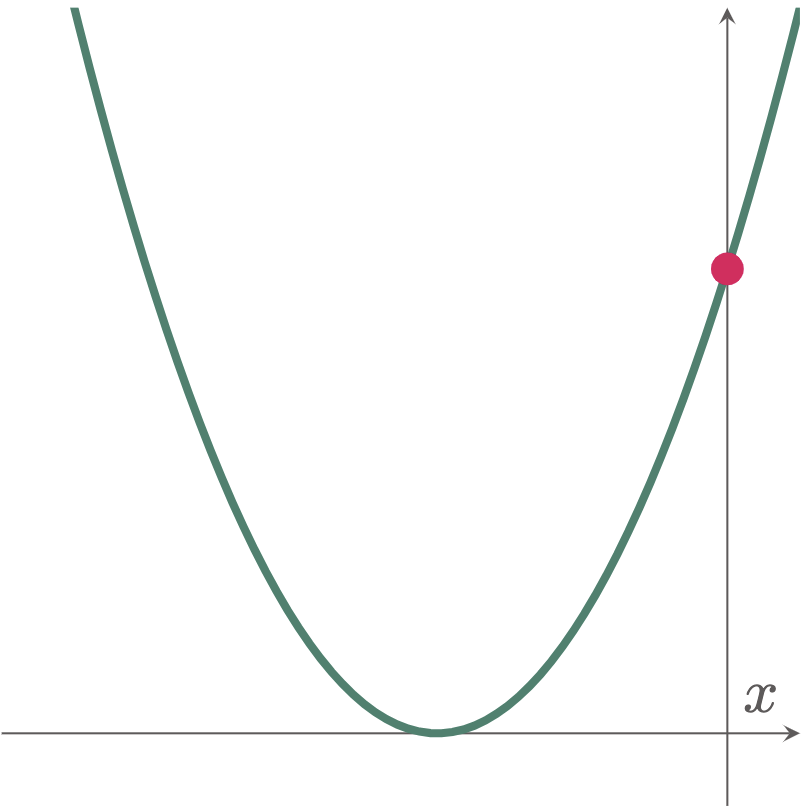
Mathematically, we can solve the intersection point by equating the equation of the curve and the $y$-axis. If you can recall, the equation of the $y$-axis is $x=0$, since every point that lies on the $y$-axis has an $x$-coordinate of 0. Thus, replacing 0 to $y=(x+4)^2$ will give us the $y$-coordinate of the intersection point.
\[\begin{align*} y &= (x+4)^2 \\ &= (0+4)^2 \\ &= 16 \end{align*}\]Hence, the point of intersection is at $(0,16)$
Since we already have the coordinates of the point, we can now solve the problem by the same method as our previous examples. To start, differentiate the equation of the curve with respect to $x$.
\[\begin{align*} \ddx\br{y} &= \ddx\brk{(x+4)^2} \\ y' &= 2(x+4) \end{align*}\]At $(0,16)$,
\[\begin{align*} m_T &= y' = 2(0+4) \\ &= 8 \end{align*}\]Solving for the equation of the tangent line using the Point-Slope Form ($\eref{eq:pt-slope of a line}$) gives us,
\[\begin{align*} y-y_1 &= m_T (x-x_1) \\ y-16 &= 8[x-0] \\ y-16 &= 8x \\ 8x-y &= -16 \tagans \end{align*}\]Then for the equation of the normal line,
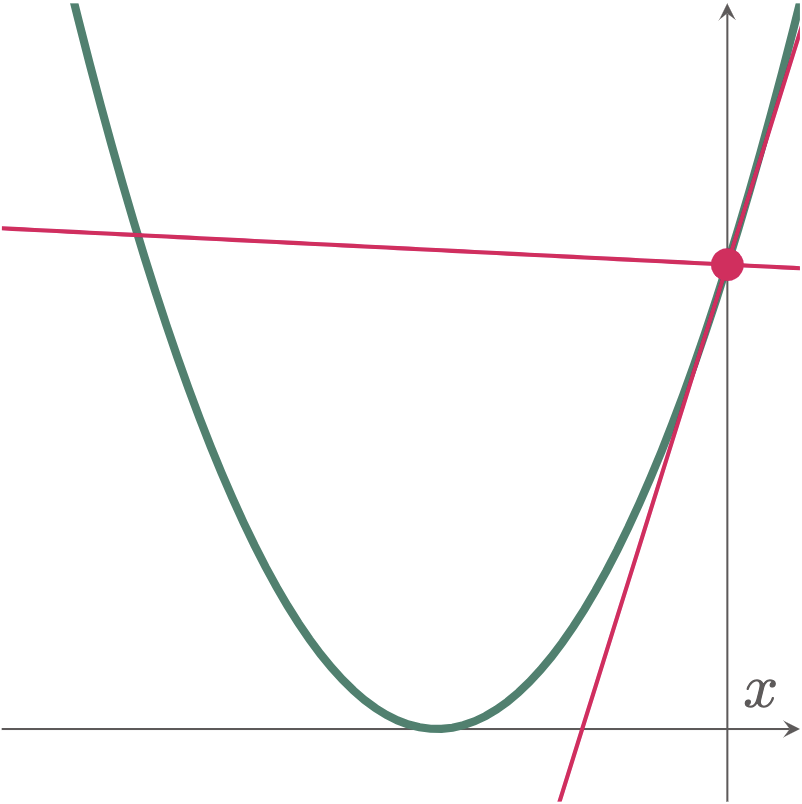
\[\begin{align*} y-y_1 &= -\frac{1}{m_T} (x-x_1) \\ y-16 &= -\frac18 (x-0) \\ 8(y-16) &= -x \\ 8y-128 &= -x \\ x+8y &= 128 \tagans \end{align*}\]To visualize, we can graph the tangent and normal lines of the curve $y=(x+4)^2$ at $(0,16)$.
$\example{4}$ Find the equation of the tangent and normal lines to the curve $a^2y-x^3=0$ at point $(a,a)$.
$\solution$
In this example, we can treat $a$ as a constant. Thus,
\[\begin{align*} \ddx\br{a^2y-x^3} &= \ddx\br{0} \\ a^2 y'-3x^2 &= 0 \\ y' &= \frac{3x^2}{a^2} \end{align*}\]To solve for the slope at $(a,a)$, we can replace $x$ and $y$ with $a$. However, in this case, we only have the variable $x$. Thus,
\[\begin{align*} m_T &= y' = \frac{3\cancel{a^2}}{\cancel{a^2}} \\ &= 3 \end{align*}\]Solving for the equation of the tangent line gives us,
\[\begin{align*} y-y_1 &= m_T (x-x_1) \\ y-a &= 3(x-a) \\ y-a &= 3x-3a \\ 3x-y &= -a+3a \\ 3x-y &= 2a \tagans \end{align*}\]Then for the equation of the normal line,
\[\begin{align*} y-y_1 &= -\frac{1}{m_T} (x-x_1) \\ y-a &= -\frac13 (x-a) \\ 3(y-a) &= -x+a \\ 3y-3a &= -x+a \\ x+3y &= 4a \tagans \end{align*}\]$\example{5}$ Find the equation of the tangent and normal lines to the curve $x^2+4x-y-2=0$ where the slope of the tangent is 6.
$\solution$
In this example, instead of having a point as one of its given, we have the slope of the tangent. To solve for the point, we can first differentiate the function.
\[\begin{align*} \ddx\br{x^2+4x-y-2} &= \ddx\br{0} \\ 2x+4-y' &= 0 \\ y' &= 2x+4 \end{align*}\]Since the tangent is equal to the derivative, we can use this parameter to solve for the $x$-coordinate of the point of tangency.
\[\begin{align*} y' &= 6 \\ 2x+4 &= 6 \\ x &= \frac{6-4}{2} \\ &= 1 \end{align*}\]Then to solve for the $y$-coordinate, substitute the value of $x$ to the equation of the curve.
\[\begin{align*} x^2+4x-y-2 &= 0 \\ y &= (1)^2+4(1)-2 \\ y &= 3 \end{align*}\]Hence, the point of tangency is at $(0,-2)$. With this, we can now solve for the equation of the tangent line.
\[\begin{align*} y-y_1 &= m_T (x-x_1) \\ y-3 &= 6 (x-1) \\ y-3 &= 6x-6 \\ 6x-y &= 3 \tagans \end{align*}\]Then for the equation of the normal line,
\[\begin{align*} y-y_1 &= -\frac{1}{m_T} (x-x_1) \\ y-3 &= -\frac16 (x-1) \\ 6(y-3) &= -x+1 \\ 6y-18 &= -x+1 \\ x+6y &= 19 \tagans \end{align*}\]$\example{6}$ At point $(1,1)$, the tangent line to the curve $y = x^3$ intersects the $x$-axis at $x=$ ?
$\solution$
In this example, we need to find the $x$-coordinate of the tangent line were it intersects the $x$-axis. To visualize, let us first try to plot the given function.
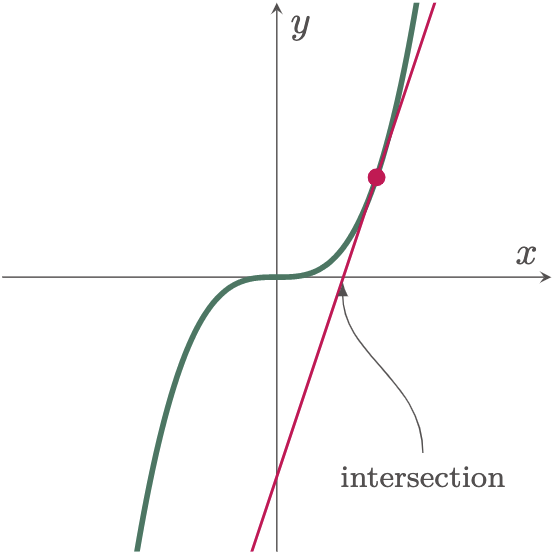
We can start by first differentiating the equation of the curve to determine its slope.
\[\begin{align*} \ddx\br{y} &= \ddx\br{x^3} \\ y' &= 3x^2 \end{align*}\]At $(1,1)$,
\[\begin{align*} m_T &= y' = 3(1)^2 \\ &= 3 \end{align*}\]Then we can now use the slope to solve for the equation of the tangent line,
\[\begin{align*} y-y_1 &= m_T (x-x_1) \\ y-1 &= 3(x-1) \\ y-1 &= 3x-3 \\ 3x-y &= 2 \end{align*}\]Since all points tha lie on the $x$-axis have a $y$-coordinate of 0, we can substitute this to the equation of the line to get its $x$-coordinate where it intersects the $x$-axis.
\[\begin{align*} 3x-(0) &= 2 \\ x &= \frac23 \tagans \end{align*}\]
