From the previous sections, we have already well established that the derivative of $y$ with respect to $x$, $\frac{dy}{dx}$ or $y’$ in Lagrange’s notation indicates the rate of change of $y$ with respect to $x$, which can also be represented graphically as the slope of a curve at a certain point. Additionally, we learned in our previous lesson that the direction of a slope is determined by its sign. With this in mind, we can tell whether a continuous curve increases or decreases based on its slope.
The function increases if the direction of the graph is going upwards. Hence, having a slope with a positive value ($y’>0$) or $y$ increases as $x$ increases will indicate that the function increases at a specific interval. On the contrary, having a slope with a negative value ($y<0$) or $y$ decreases as $x$ increases will indicate that the function decreases at a specific interval.
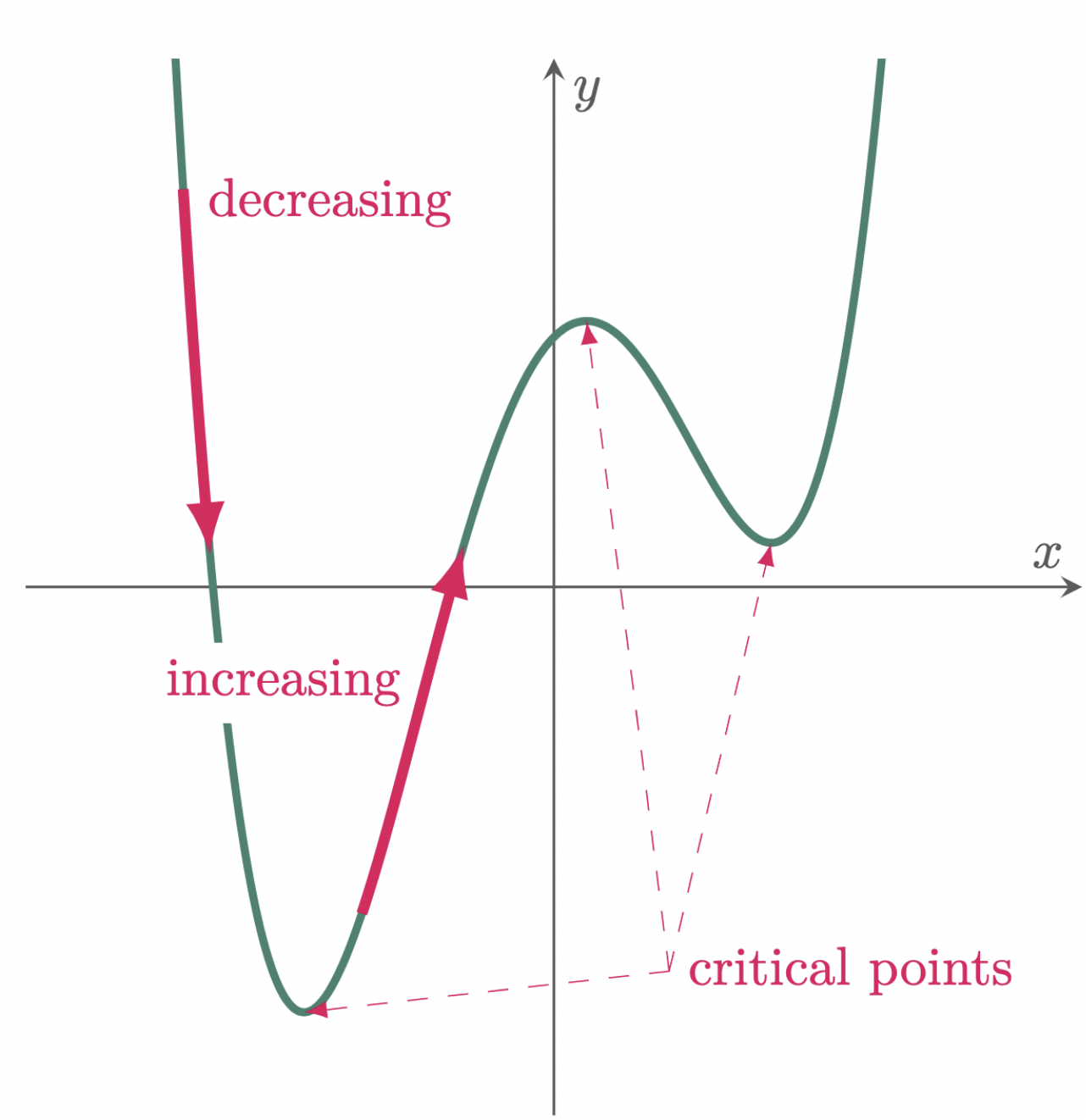
Figure 1: Increasing and decreasing
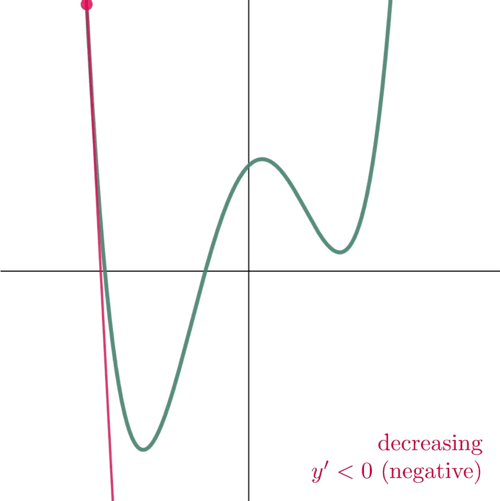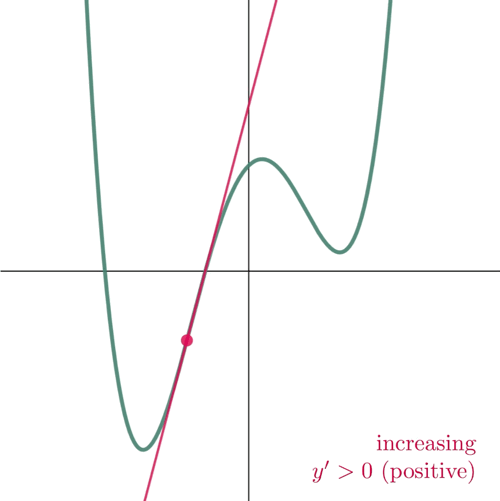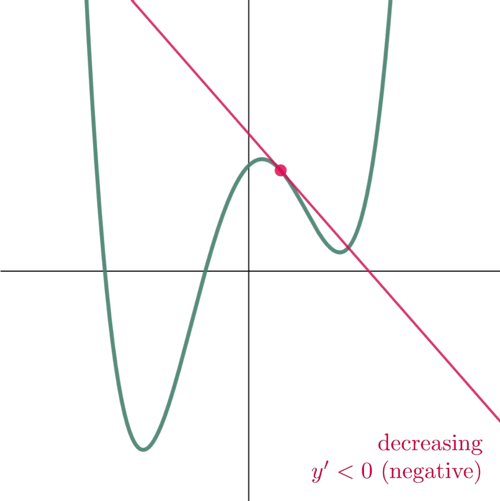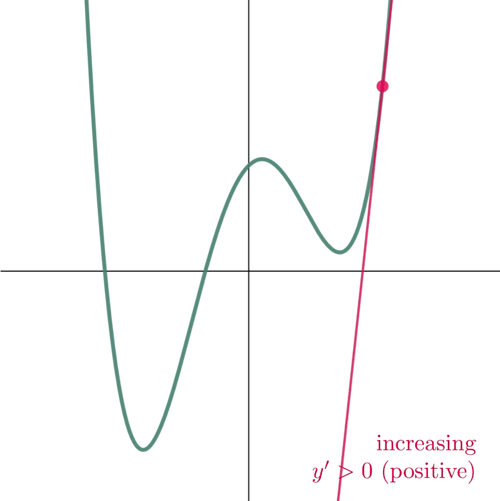
Figure 2: At the point where the slope is positive, the function increases. And where the slope is negative, the function decreases.
However, a function can increase in two ways: either increasing at a decreasing rate ($\fref{3a}$) or increasing at an increasing rate ($\fref{3b}$). Similarly, a function can also decrease at a decreasing rate ($\fref{3c}$) or decrease at an increasing rate ($\fref{3d}$). The direction of a function can reveal a great deal about it, particularly when it comes to identifying the graph’s behavior, which is very valuable when sketching curves.
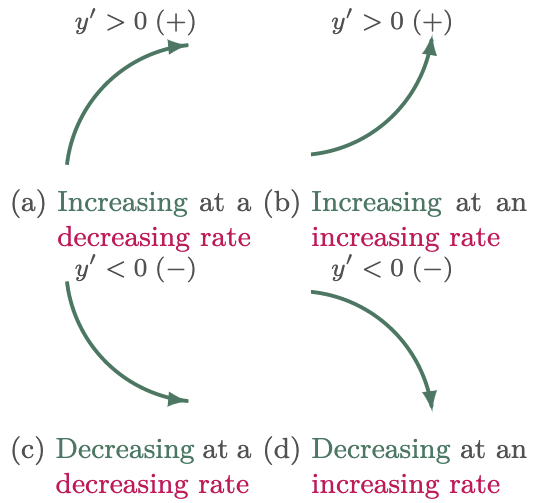
Figure 3: Direction of increasing and decreasing functions

