Maxima and Minima are the critical points found on a polynomial curve, collectively known as extremes. Moreover, since critical points can occur multiple times on a curve, we can classify the points by either relative or absolute.
Relative maximum are points that are higher relative to its neighboring points, while relative minimum are points that are lower relative to its neighboring points $(\fref{1})$. In contrast, absolute maximum and absolute minimum are the largest and smallest valued extremes in the function’s entire domain $(\fref{2})$.
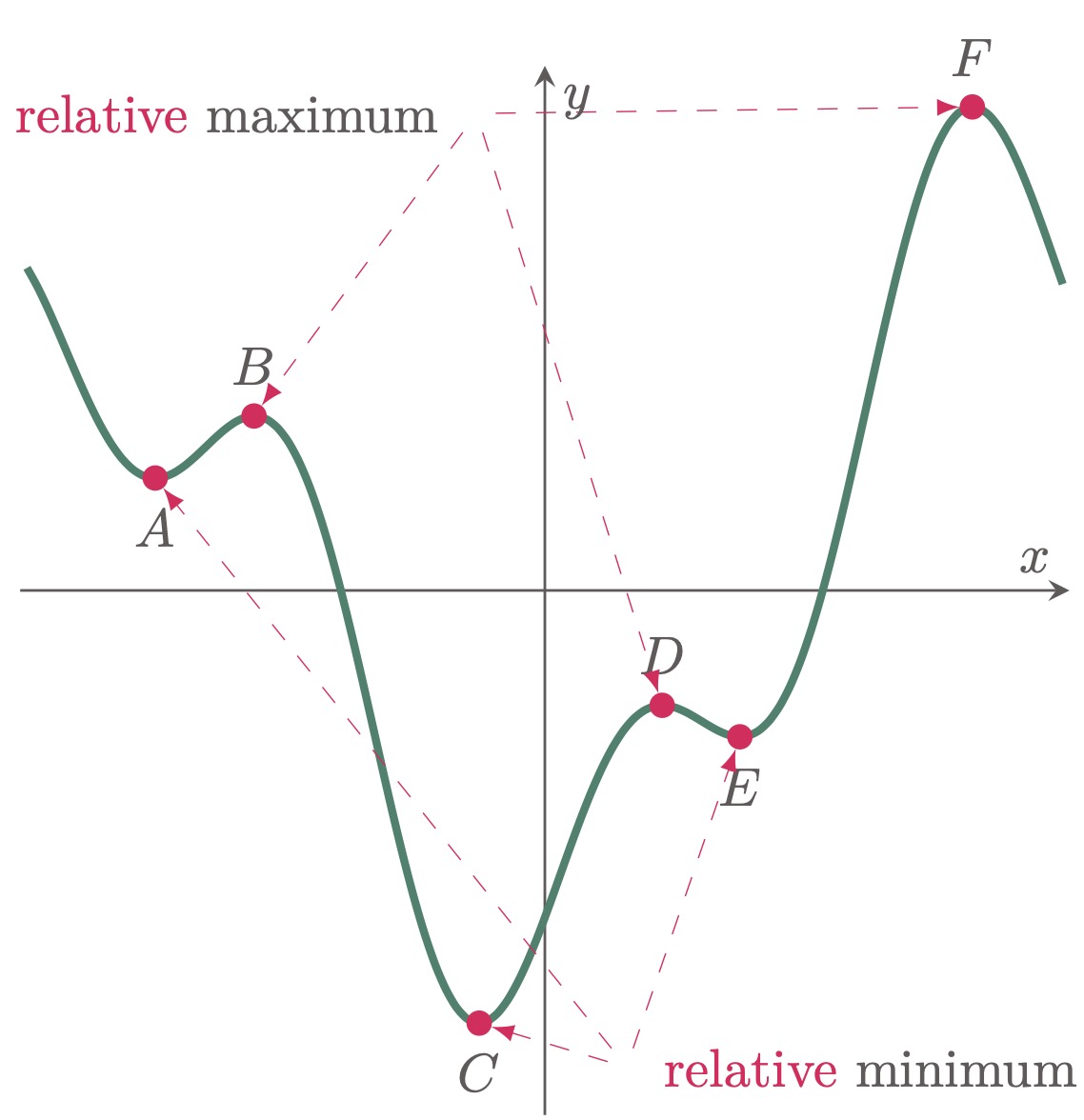
Figure 1: Points $B$, $D$, and $F$ are relative maximum. And points $A$, $C$, and $E$ are relative minimum
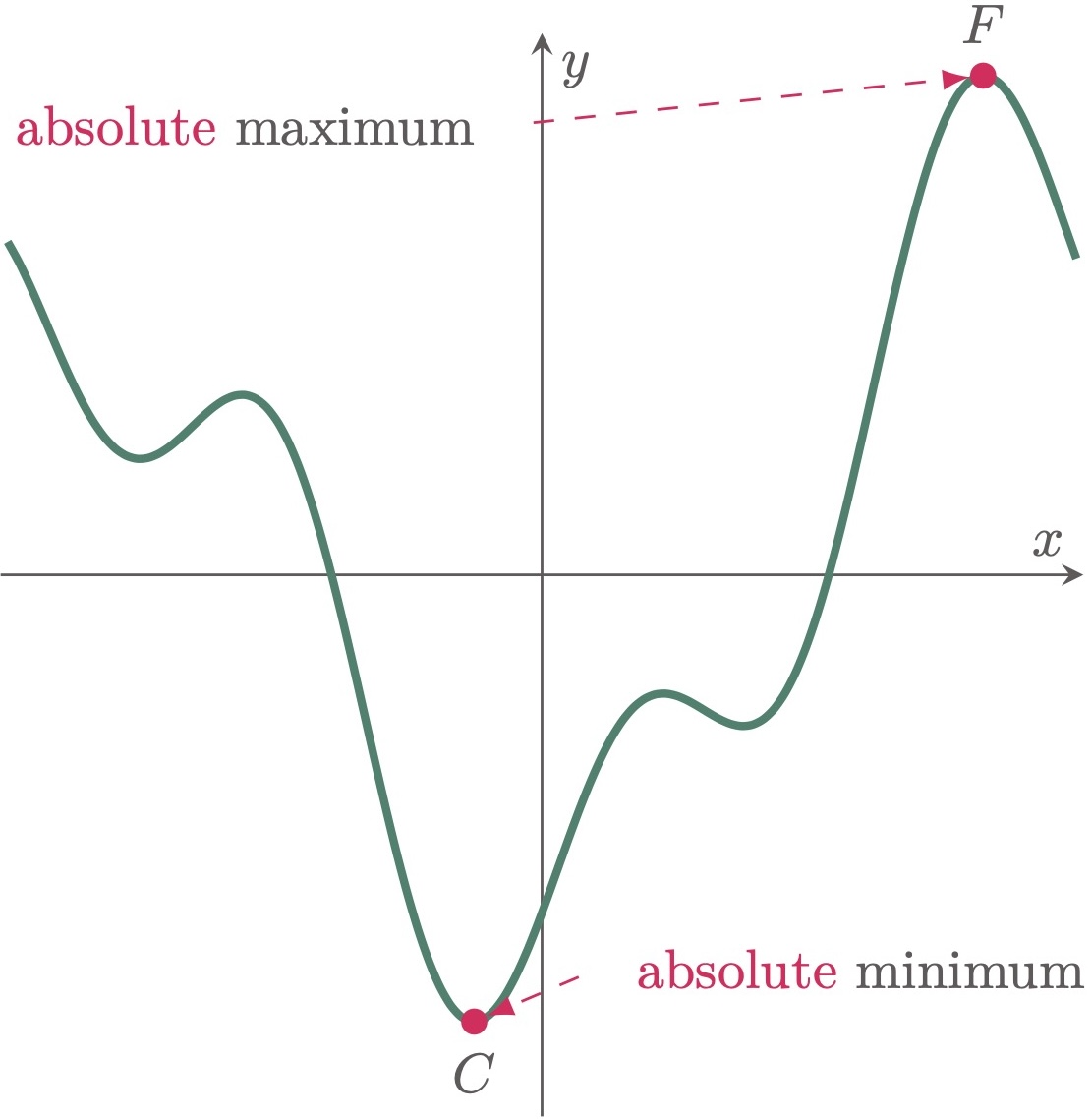
Figure 2: Points $C$ and $F$ are the absolute minimum and maximum points respectively
What’s interesting about these critical points is that both maxima and minima are found at the peaks of the curve, where the slopes of the tangent lines are parallel to the $x$-axis, thus having a slope equal to zero $(\fref{3})$. Understanding where these critical points lie is essential since they indicate where a function reaches its extreme values, which is invaluable in many real-world applications that we will cover in the next chapter. In this section, however, we will first focus our attention on locating these points on the curve.
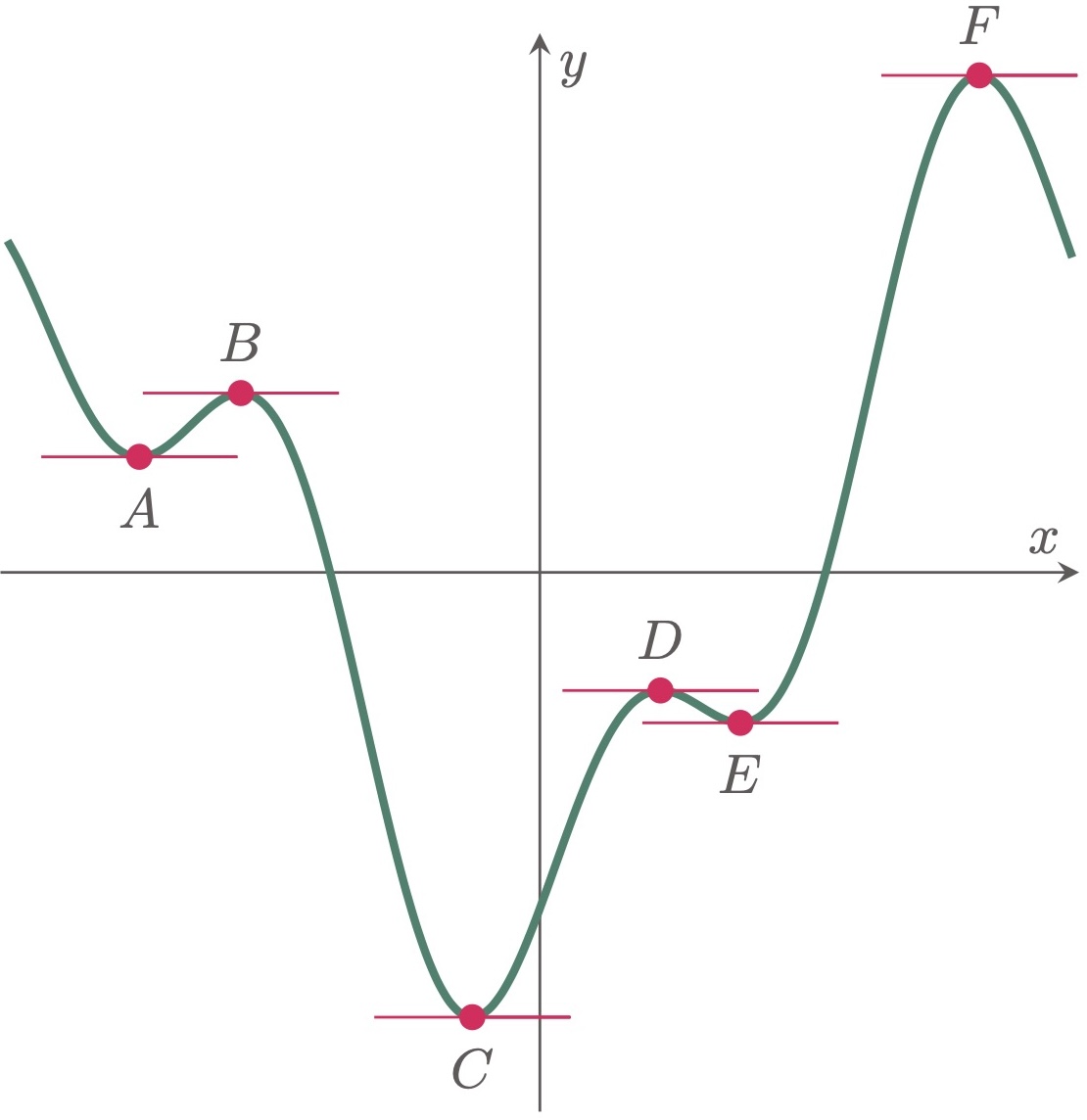
Figure 3: For every critical point, it has a slope of $\dydx = 0$
$\example{1}$ Locate the critical point/s of the curve, $y = 3x^2-6x+9$
$\solution$
To determine the critical point(s) of the curve, we know that points lying at the peaks of the curve have a slope of zero. With this in mind, we can first differentiate the function to find the slope at any point:
\[\begin{align*} \ddx\br{y} &= \ddx\br{3x^2-6x+9} \\ \dydx &= 6x-6 \end{align*}\]At the critical point(s), the slope is $\dydx = 0$. Thus,
\[\begin{align*} 0 &= 6x-6 \\ 6x &= 6 \\ x &= 1 \\ \end{align*}\]To determine the $y$-coordinate of the critical point, we can substitute this value of $x$ to the given function.
\[\begin{align*} y &= 3(1)^2-6(1)+9 \\ &= 6 \end{align*}\]Hence, the coordinate of the critical point of the function $y = 3x^2-6x+9$ is at $(1,6)$.
This method only tells you where the critical point is, but it cannot determine whether it is a maximum or a minimum. To determine the nature of the critical point, we can utilize a simple test known as the second derivative test.

