Optimization involves finding the best solution under a given set of constraints. It answers critical questions like: What dimensions should a container have to maximize its volume while using the least amount of material? or How can a company minimize costs while maximizing profits? By using derivatives, we can find the maximum and minimum values of functions, enabling us to make optimal decisions in various contexts.
In the chapter “Polynomial Curves,” we discussed how to find the maximum and minimum points of a specific function, which are points that occur where the slope of the curve is zero. This property is at the heart of optimization. As long as we can express a specific problem as a function, we can analyze how the system behaves and determine optimal solutions.
In optimization problems, the usual goal is to find the value of the independent variable that results in the dependent variable being either at a maximum or a minimum. To understand this, let’s explore the general steps involved in solving optimization problems and then look at some examples.
General Steps in Solving Optimization Problems
Before diving into the examples, it would be best to outline first the general steps involved in solving optimization problems:
- Understand the Problem. Carefully read the problem to determine what quantity needs to be optimized (maximized or minimized) and identify the variables involved.
- Formulate the Function. Express the quantity you need to optimize as a function of the variable you want to optimize. For instance, if we want to maximize the area, then the area should be isolated on one side of the equation.
- Identify the Relationships. Use any given relationships or constraints to eliminate variables and write the function in terms of a single variable.
- Find the Critical Points. Apply the concept of maxima and minima to determine the value of the independent variable.
- Test the Critical Points. Use the second derivative test to determine if the critical point corresponds to a maximum or a minimum.
- Answer the Question. Provide the final answer, ensuring it addresses what is required in the problem.
$\example{1}$ Determine the values of two numbers if their sum is 8, and the product of one number and the cube of the other is maximized.
$\solution$
In this example, we want to maximize the product of one number and the cube of the other. We can set the first number to be $x$, and the other to be $y$. Thus:
\[\begin{align*} M &= xy^3 \tag{eq.1} \end{align*}\]We can use another relationship, $x + y = 8$, to reduce the number of variables to only one. In our case, it would be easier to replace the value of $x$ to simplify the solution. Hence, we can isolate $x$:
\[\begin{align*} x &= 8 - y \tag{eq.2} \end{align*}\]Substitute this into equation (eq.1):
\[\begin{align*} M &= (8 - y) y^3 \\ &= 8y^3-y^4 \end{align*}\]To maximize the value of $M$, differentiate the function with respect to the independent variable $y$.
\[\begin{align*} \ddx\br{M} &= \ddx{8y^3-y^4} \\ \frac{dM}{dy} &= 24y^2-4y^3 \\ \end{align*}\]To determine the critical value, set $\frac{dM}{dy} = 0$.
\[\begin{align*} 0 &= 24y^2-4y^3 \\ 0 &= 4y^2(6-y) \\ \implies 0 &= 4y^2 \qquad;\quad 0 = 6-y \\ y &= 0 \quad\qquad;\quad y = 6 \end{align*}\]In this case, 0 cannot be possible since it will make the value of M to be zero, which most probably not be maximized. Thus, $y = 6$. With this, we can now substitute the value into equation (eq.2) to solve for the other number.
\[\begin{align*} x &= 8 - y \\ &= 8 - 6 \\ &= 2 \end{align*}\]Hence, the values of the two numbers are 6 and 2 that satisfies the problem.
$\example{2}$ A homeowner only has 10 meters of fencing to build a rectangular garden, using two existing perpendicular walls as two sides of the rectangle. What dimensions will maximize the area of the garden?
$\solution$
In this type of problem, it is helpful to start by drawing a simple sketch to clearly represent the situation. The sketch should include all given values and any necessary variables for unknown values that will help in solving the problem. In this case, we want to maximize the total area of the garden, so we need to express the area in terms of the dimensions of the rectangle.
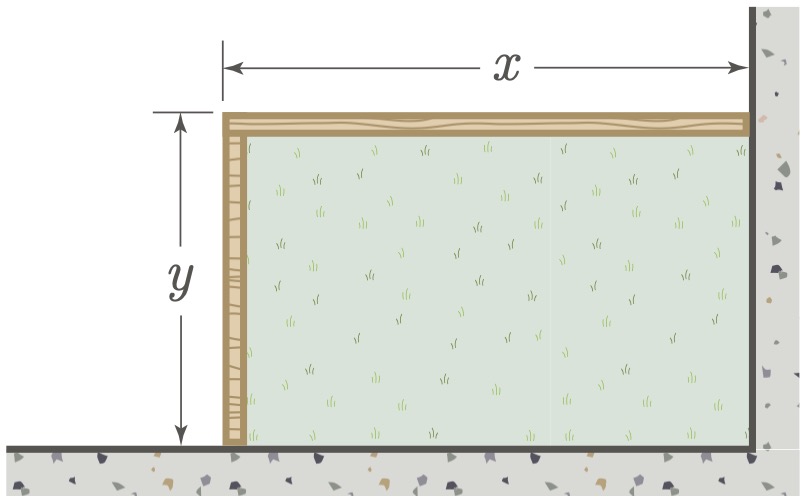
Given that we have 10 meters of fencing material and only two sides of the garden need to be fenced (since the other two sides are formed by the walls), we can reduce the number of variables. We express one variable in terms of the other. In this case, let $y = 10 - x$.
\[\begin{align*} A &= x(10-x) \\ \end{align*}\]Since we want to maximize the area and now have $A$ expressed as a function of one variable $x$, we can differentiate the function with respect to $x$.
\[\begin{align*} \ddx\br{A} &= \ddx\brk{x(10-x)} \\ \frac{dA}{dx} &= x(-1)+(10-x) \\ &= 10-2x \end{align*}\]To find the critical point, set $\frac{dA}{dx} = 0$:
\[\begin{align*} 0 &= 10-2x \\ x &= 5 \tagans \end{align*}\]Now, substituting the value of $x$ back into $y = 10 - x$, we get $y = 0$
Hence, to maximize the area of the garden with the given material, the dimensions should be $10\un{m} \x 10\un{m}$, resulting in a total area of $100\un{m^2}$
$\example{3}$ Two poles, one 18 meters high and the other 12 meters high, stand 40 meters apart. They are to be supported by wires attached to a single anchor point on the ground between them, with wires running from the tops of the poles to the anchor point. Where should the anchor point be placed along the line between the poles to use the least amount of wire?
$\solution$
In this case, we want to minimize the total length of the wire, so we need to express the total wire length as a function of the position of the anchor point, which we represent as $x$ along the line between the poles.
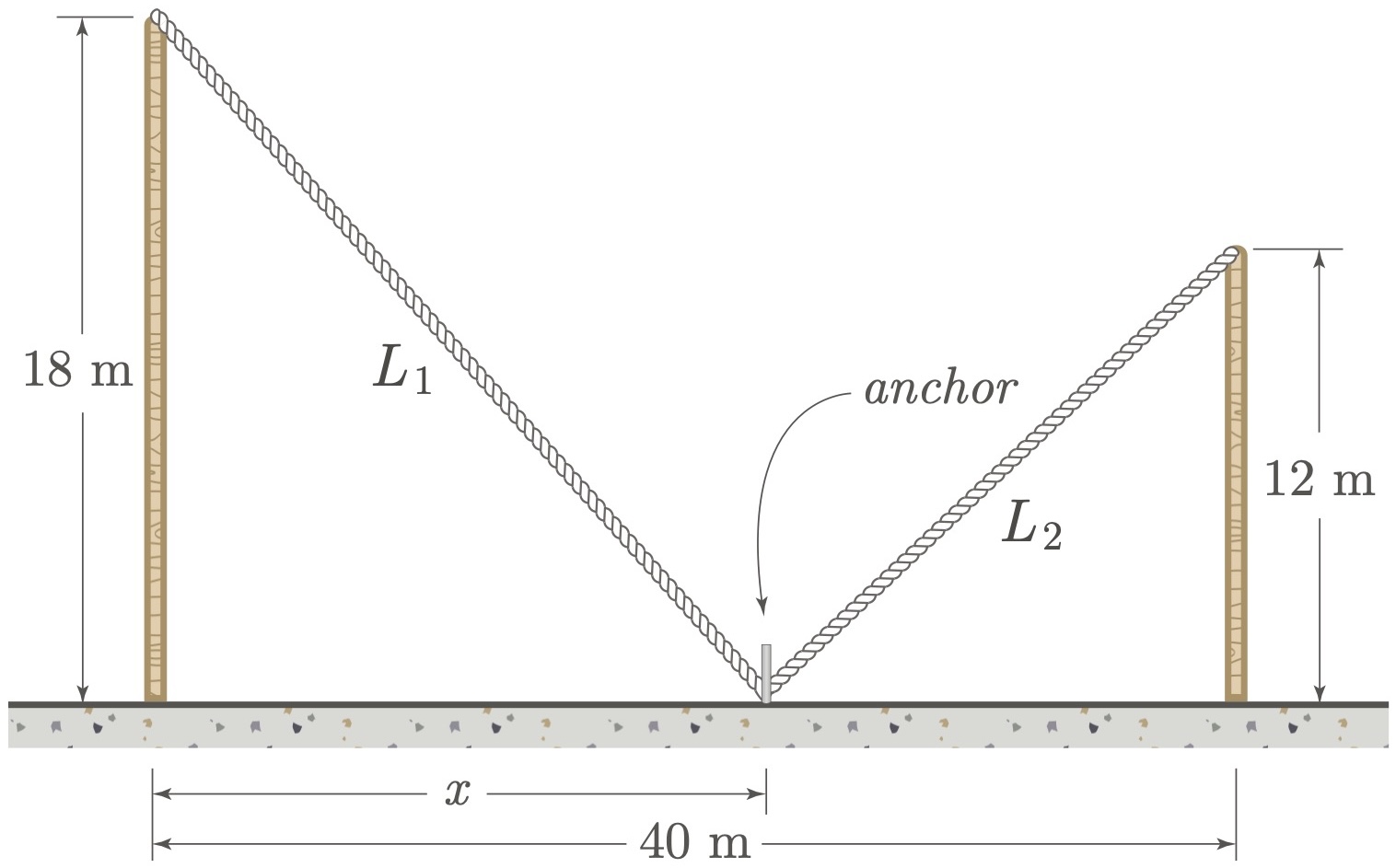
To derive an equation for the total length of the wire, we can assume that the poles are perpendicular to the ground. Using the Pythagorean theorem, we can calculate the length of each wire as the hypotenuse of a right triangle. Thus, the total length of the wire is the sum of the two hypotenuses formed by these triangles.
\[\begin{align*} L &= L_1+L_2 \\ L &= \sqrt{18^2+x^2}+\sqrt{12^2+\br{40-x}^2} \\ L &= \br{324+x^2}^{\frac12}+\brk{144+\br{40-x}^2}^{\frac12} \end{align*}\]Since we want to minimize the total wire length, and now have $L$ expressed as a function of the position of the anchor point $x$, we can proceed by differentiating the function with respect to $x$.
\[\begin{align*} \ddx\br{L} &= \ddx\brk{\br{324+x^2}^{\frac12}+\brk{144+\br{40-x}^2}^{\frac12}} \\ \frac{dL}{dx} &= \frac12(324+x^2)^{-\frac12}(2x)+\frac12\brk{144+\br{40-x}^2}^{-\frac12}\bbrk{2(40-x)(-1)} \\ \frac{dL}{dx} &= \frac{2x}{2(324+x^2)^{-\frac12}}+\frac{2(40-x)(-1)}{2\brk{144+\br{40-x}^2}^{-\frac12}} \end{align*}\]To find the extreme point, we set $\frac{dL}{dx} = 0$.
\[\begin{align*} 0 &= \frac{x}{\sqrt{324 + x^2}} - \frac{(40 - x)}{\sqrt{144 + (40 - x)^2}} \\ \frac{x}{\sqrt{324 + x^2}} &= \frac{(40 - x)}{\sqrt{144 + (40 - x)^2}} \\ \brk{x{\sqrt{144 + (40 - x)^2}}}^2 &= \brk{(40 - x){\sqrt{324 + x^2}}}^2 \\ x^2\br{144 + (40 - x)^2} &= (40 - x)^2\br{324 + x^2} \\ 144x^2 + \cancel{x^2(40 - x)^2} &= 324(40 - x)^2 + \cancel{x^2(40 - x)^2} \\ 144x^2 &= 324(1600-80x+x^2) \\ 4x^2 &= 9(1600-80x+x^2) \\ 0 &= 14,\,400-720x+5x^2 \\ 0 &= x^2-144x+2880 \\ 0 &= (x-24)(x-120) \\ \implies x &= 24 \quad;\quad x=120 \end{align*}\]Since the value of $x$ must be less than 40, the only logical solution is $x = 24$. This means that the anchor point is located 24 meters from the 18-meter pole, resulting in the least amount of wire being used.
$\example{4}$ Determine the diameter of a closed cylindrical can that can hold $500\un{cm^3}$ of milk, such that the least amount of material is used to manufacture it.
$\solution$
We need to determine the diameter of the cylinder that minimizes the surface area $A$. To do this, we need to express $A$ as a function of the diameter $D$. To start, we analyze the equation for the surface area $A$ of a closed cylinder (including the top and bottom).
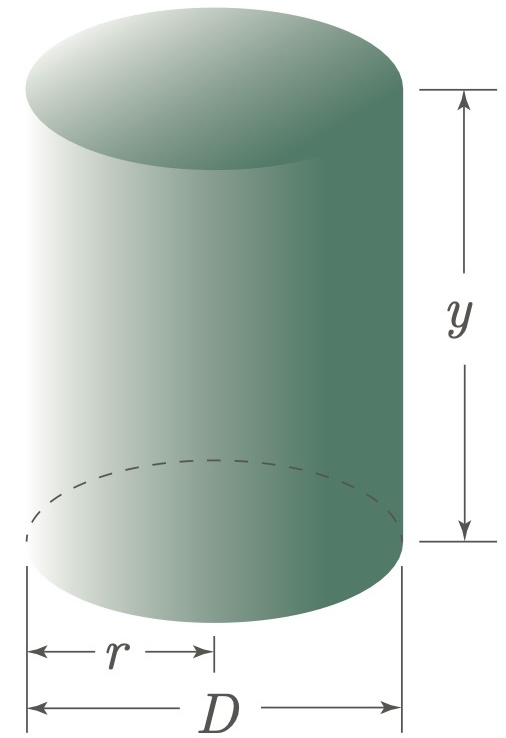
In this equation, there are two variables, the radius $r$ and the height $h$. Since we want to express A as a function of the diameter $D$, and the radius is half of the diameter, our focus shifts to expressing $h$ in terms of $r$. We can use the given volume to find an expression for $h$.
\[\begin{align*} V &= \pi r^2h \\ h &= \frac{V}{r^2} \end{align*}\]Given that the volume is fixed at $500\un{cm^3}$, substituting this into the equation gives us:
\[\begin{align*} h &= \frac{500}{r^2} \tag{eq.2} \end{align*}\]Subtitute this value to eq.1.
\[\begin{align*} A &= 2\pi r^2 + 2\pi r \br{\frac{500}{r^2}} \\ &= 2\pi r^2 + \frac{1000}{r} \end{align*}\]Next, to express the surface area as a function of $D$, we replace $r$ with $\frac{D}{2}$:
\[\begin{align*} &= 2\pi\br{\frac{D}{2}}^2 + \frac{1000(2)}{D} \\ &= \frac{\pi D^2}{2} + \frac{2000}{D} \\ \end{align*}\]We can now differentiate the function with respect to the diameter $D$.
\[\begin{align*} \frac{d}{dD}\br{A} &= \frac{dA}{dD}\br{\frac{\pi D^2}{2} + 2000D^{-1}} \\ \frac{dA}{dD} &= \frac{2\pi D}{2} - 2000D^{-2} \\ &= \pi D - \frac{2000}{D^{2}} \end{align*}\]To find the extreme point, we set $\frac{dA}{dD} = 0$.
\[\begin{align*} 0 &= \pi D - \frac{2000}{D^{2}} \\ \pi D &= \frac{2000}{D^{2}} \\ D &= \sqrt[3]{\frac{2000}{\pi}}\un{cm} \\ &\approx 8.6\un{cm} \end{align*}\]Hence, the can that can hold a volume of $500\un{cm}^3$ using the least amount of material has a diameter of $\sqrt[3]{\frac{2000}{\pi}}\un{cm}$, or approximately 8.6 cm.

