Another application of derivatives is related rates. It deals with situations on how two or more variables change in relation to each other with respect to time. The main idea is that using calculus we can deduce or calculate the rate of change of one quantity by observing the rate of change of a related quantity that can be observed more easily. This is anchored on the fact that, in everyday life, many phenomena involve quantities that are interdependent and changing, i.e., when one variable changes, it often triggers a change in another.
For instance, how does the area of a circle change as its radius expands over time? If water is being poured into a conical tank, how does the water level rise as the volume increases? By understanding the relationships between the rates at which variables change, we can analyze and predict the behavior of dynamic systems.
The related rates problems are solved using derivatives, specifically by applying implicit differentiation with respect to time.
General Steps in Solving Optimization Problems
Before diving into the examples, it would be best to outline first the general steps involved in solving optimization problems:
- Understand the problem. Read the problems carefully and identify the quantities involved, how they are related and their rates of change. It often requires you to have strong background of formula on how these quantities relate to each other, e.g., velocity, volume, area, and others.
- Draw a diagram. Draw a diagram whenever applicable. This helps you visualize the relationships between the different quantities, and establish the variables needed. In this step, you can also write the known and unknown values stated in the problem.
- Write an equation that relates the quantities. This is typically a geometric or algebraic relationship between the variables (e.g., the Pythagorean theorem, volume formulas, etc.).
- Differentiate the equation with respect to time. Use implicit differentiation to find the rate of change of one variable concerning time. Remember to apply the chain rule.
- Substitute the known values. Plug in the given rates and other known values from the problem into the differentiated equation.
- Solve for the unknown rate. Isolate the desired rate of change and solve.
$\example{1}$ A 10-meter long ladder is leaning against a vertical wall. The bottom of the ladder is sliding away from the wall at a rate of 2 meter per second. How fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 meters from the wall?
$\solution$
Let $x$ be the distance from the bottom of the ladder to the wall, and $y$ be the height of the top of the ladder above the ground. With this, we can represent the rate of sliding from the wall as $\frac{dx}{dt}$ (which we already have a value of 2 m/s), and the rate of the ladder sliding down as $\frac{dy}{dt}$ (which is required).
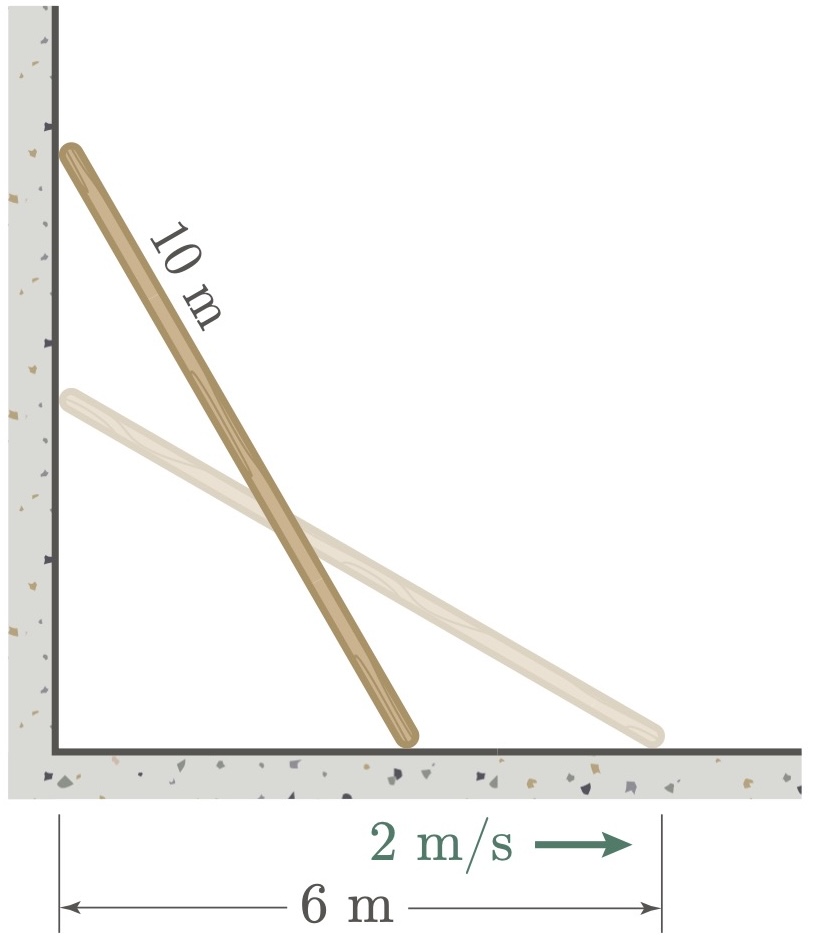
After sketching the figure, notice that the ladder forms a right triangle with the wall and the ground, so by the Pythagorean theorem:
\[\begin{align*} x^2+y^2 &= 10^2 \\ x^2+y^2 &= 100 \\ \end{align*}\]Differentiating the function with respect to time gives us:
\[\begin{align*} \ddt\br{x^2+y^2} &= \ddt\br{100} \\ 2x\frac{dx}{dt}+2y\frac{dy}{dt} &= 0 \\ 2y\frac{dy}{dt} &= -2x\frac{dx}{dt}\\ \frac{dy}{dt} &= -\frac{x}{y}\frac{dx}{dt} \tag{eq.1} \end{align*}\]Applying the Pythagorean theorem again to solve for the height of the ladder when $x = 6$.
\[\begin{align*} y^2 &= 100-y^2 \\ y &= \sqrt{100-6^2} \\ &= 8 \end{align*}\]Now, substitute these values into the eq.1 to get the rate of the ladder sliding down the wall $\frac{dy}{dt}$.
\[\begin{align*} \frac{dy}{dt} &= -\frac{6}{8}(2) \\ \frac{dy}{dt} &= -\frac32\un{m/s} \\ &= -1.5\un{m/s} \end{align*}\]The negative sign denotes the direction of the motion, which in this case, it is going down, therefore, we can say that the ladder is “sliding down” at the rate of 1.5 m/s.
$\example{2}$ Air is being pumped into a spherical balloon so that its volume increases at a rate of 50 cubic centimeters per second. How fast is the radius of the balloon increasing when the radius is 5 centimeters?
$\solution$
Recall that the volume of a sphere is given by the equation:
\[\begin{align*} V &= \frac43\pi r^3 \end{align*}\]In this equation, we see the relationship between the volume and the radius of the sphere. The question is how to relate the rate of change of the volume, $\frac{dV}{dt}$, to the rate of change of the radius, $\frac{dr}{dt}$. To find this relationship, we differentiate the volume equation with respect to time.
\[\begin{align*} \ddt\br{V} &= \ddt\br{\frac43\pi r^3} \\ \frac{dV}{dt} &= 4\pi r^2 \frac{dr}{dt} \\ \end{align*}\]In the given problem, $\frac{dV}{dt}$ is provided as $50\un{cm^3/s}$, and we want to determine $\frac{dr}{dt}$.
\[\begin{align*} \frac{dr}{dt} &= \frac{dV/dt}{4\pi r^2} \end{align*}\]Substituting the known values to the equation gives us:
\[\begin{align*} \frac{dr}{dt} &= \frac{50}{4\pi (5)^2} \\ &= \frac{50}{100\pi} \\ &= \frac{1}{2\pi}\un{cm/s} \end{align*}\]The positive sign indicates that the radius is increasing; therefore, the radius of the balloon is increasing at a rate of $\frac{1}{2\pi}\un{cm/s}$.
$\example{3}$ A car is traveling north at 40 km/h, while another car is traveling east at 50 km/h. How fast is the distance between the cars increasing when the car traveling north is 75 km from the intersection, and the car traveling east is 100 km from the intersection?
$\solution$
rom the given problem, the rate of the car traveling north is $\frac{dy}{dt} = 40\un{km/h}$, with a current distance from the intersection of $y = 75\un{km}$. For the car traveling east, $\frac{dx}{dt} = 50\un{km/h}$, with a current distance from the intersection of $x = 100\un{km}$. We can represent the distance between the two cars as $z$.
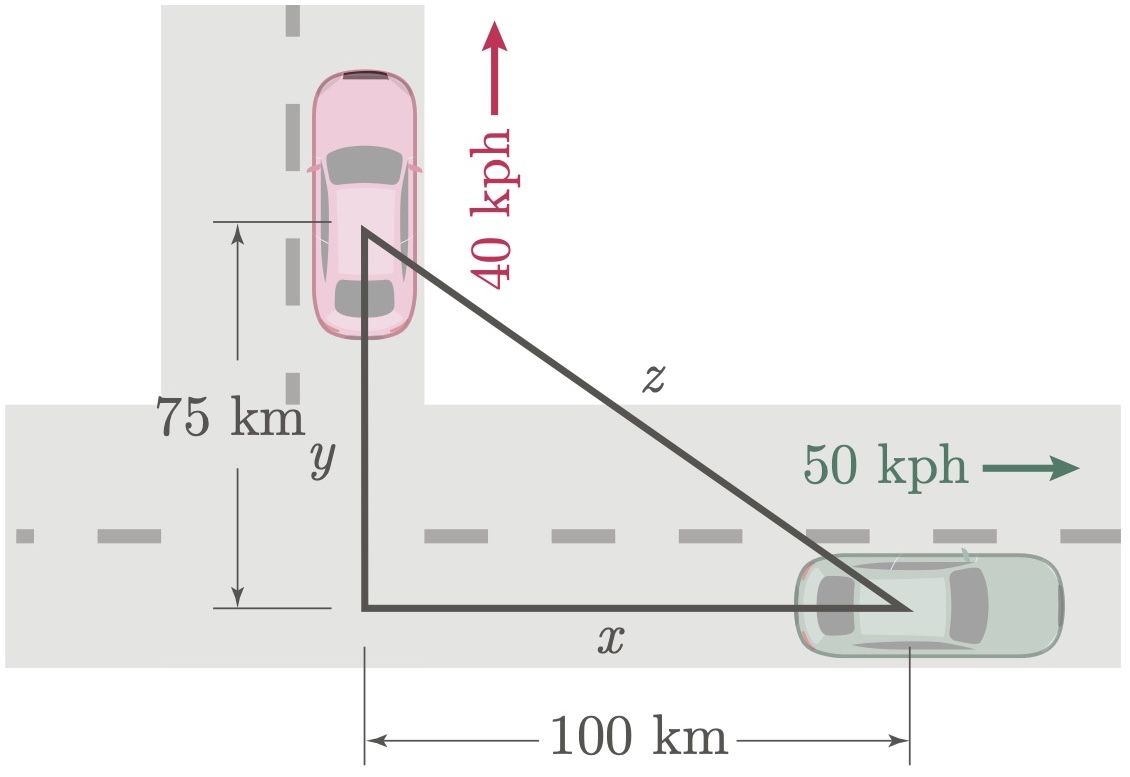
The relationship between the distances can be expressed using the Pythagorean theorem:
\[\begin{align*} z^2 &= x^2+y^2 \end{align*}\]Differentiate both sides of the equation with respect to time $t$:
\[\begin{align*} 2z\frac{dz}{dt} &= 2x\frac{dx}{dt}+2y\frac{dy}{dt} \\ z\frac{dz}{dt} &= x\frac{dx}{dt}+y\frac{dy}{dt} \\ \frac{dz}{dt} &= \frac{x\frac{dx}{dt}+y\frac{dy}{dt}}{z} \tag{eq.1} \end{align*}\]Use the Pythagorean theorem again to calculate the value of $z$ when $x = 100\un{km}$ and $y = 75\un{km}$,
\[\begin{align*} z &= \sqrt{100^2+75^2} \\ &= 125\un{km} \end{align*}\]Substitute the known values to eq.1:
\[\begin{align*} \frac{dz}{dt} &= \frac{100(50)+75(40)}{125} \\ &= 64\un{km/hr} \end{align*}\]Therefore, the distance between the two cars is increasing by a rate of 64 km/hr.
$\example{4}$ A conical tank with a height of 10 meters and a base radius of 4 meters is being filled with water at a rate of 2 cubic meters per minute. How fast is the water level rising when the water is 5 meters deep?
$\solution$
The volume $V$ of water in a cone is given by:
\[\begin{align*} V &= \frac13\pi r^2h \end{align*}\]Since the radius $r$ of the water surface changes as the height $h$ changes, we need to express $r$ in terms of $h$ using the geometry of the cone. From the given problem, the radius of the cone at its full height (10 m) is 4 m. So, the radius and height of the water form similar triangles with the full cone. Thus, the ratio of radius to height is constant:
\[\begin{align*} \frac{r}{h} &= \frac{4}{10} \\ r &= \frac{4}{10}h \\ r &= \frac25h \end{align*}\]Substituting this into the original equation, we get:
\[\begin{align*} V &= \frac13\pi \br{\frac25h}^2h \\ V &= \frac13\pi \br{\frac{4}{25}h^2}h \\ V &= \frac{4\pi}{75}h^3 \end{align*}\]Differentiating this with respect to time,
\[\begin{align*} \ddt\br{V} &= \ddt\br{\frac{4\pi}{75}h^3} \\ \frac{dV}{dt} &= \frac{4\pi}{75}\cdot3h^2\frac{dh}{dt} \\ \frac{dV}{dt} &= \frac{4\pi}{25}h^2\frac{dh}{dt} \end{align*}\]Isolating $\frac{dh}{dt}$:
\[\begin{align*} \frac{dh}{dt} &= \frac{25}{4\pi h^2}\frac{dV}{dt} \end{align*}\]Substituting the known values,
\[\begin{align*} \frac{dh}{dt} &= \frac{25}{4\pi (5)^2}(2) \\ &= \frac{1}{2\pi}\un{m/min} \end{align*}\]Hence, at a water level of 5 m, the rate of the water level rising is $\frac{1}{2\pi}\un{m/min}$.

