We have already dealt with algebraic functions from the previous lessons, so we are no longer strangers with terms containing exponents. For example, in the function $f(x)=x^2$, the exponent of the independent variable $x$ is 2. Now consider an exponential function, such as $g(x)=2^x$. The latter example shows that the independent variable is now the exponent in the function. This minor distinction between the two functions has a significant effect on how the function behaves. Furthermore, Exponential Functions is written in the form,
$$\begin{align} f(x) = a^x, \quad\text{where: $a>0$ and $a \neq 1$} \end{align}$$
Before we start our lesson, let us have a simple example to appreciate the importance of an exponential function. Consider the following scenario: you’ve decided to start a networking business and have initially hired five (5) employees. To break even, they must each recruit five (5) individuals, and each recruitee must likewise recruit five (5) people. As a result, your business grows at a rate of $f(x)=5^x$.
Having the ability to express your business mathematically helps us calculate the revenue of the company. However, this is just one instance of how exponential functions may be advantageous. There are many more, but before we can evaluate problems in exponential functions, we must first be familiar with some of the fundamental laws of exponents and radicals.
Basic Laws of Exponents and Radicals
$\tcBal{Laws of Exponents}$ $$ \begin{align} a^m \cdot a^n &= a^{m+n} \\ \frac{a^m}{a^n} &= a^{m-n} \\ (a^m)^n &= a^{mn} \\ \br{ \frac{a}{b} }^n &= \frac{a^n}{b^n} \\ a^{\frac{m}{n}} &= \sqrt[n]{a^m} \\ a^{-n} &= \frac{1}{a^n} \\ a^0 &= 1 \end{align} $$
$\tcBal{Laws of Radicals}$ $$ \begin{align} \sqrt[n]{a} &= a^{\frac{1}{n}} \\ \sqrt[n]{a^m} &= \br{ \sqrt[n]{a} }^m \\ \sqrt[n]{a^n} &= a \\ \sqrt[n]{a} \cdot \sqrt[n]{b} &= \sqrt[n]{ab} \\ \frac{\sqrt[n]{a}}{\sqrt[n]{b}} &= \sqrt[n]{\frac{a}{b}} \; : b\neq 0 \\ \sqrt[-n]{a} &= \frac{1}{\sqrt[n]{a}} \\ \sqrt[1]{a} &= a \end{align} $$
$\example{1}$ Solve for $x$, $7^{x-1}=7^{4x}$.
$\solution$
Since the base of all the terms are the same, equate its exponents,
\[\begin{align*} x-1 &= 4x \\ 4x-x &= -1 \\ x &= -\frac{1}{3} \tagans \end{align*}\]$\example{2}$ Solve for $x$, $5^{1-x}=25$
$\solution$
Express 25 as $5^2$ to match the base of the other term,
\[\begin{align*} 5^{1-x} &= 5^2 \end{align*}\]And since all the terms have the same base, equate its exponents,
\[\begin{align*} 1-x &= 2 \\ x &= 1-2 \\ &= -1 \tagans \end{align*}\]$\example{3}$ Solve for $x$, $4^{3x-1} = 8^{x}$
$\solution$
Express all the terms as base of 2,
\[\begin{align*} 2^{2(3x-1)} &= 2^{3x} \end{align*}\]Then equate its exponents,
\[\begin{align*} 2(3x-1) &= 3x \\ 6x-2 &= 3x \\ 3x &= 2 \\ x &= \frac{2}{3} \tagans \end{align*}\]$\example{4}$ Solve for $x$, $3^{5-2x} = \frac{1}{27}$
$\solution$
Get the reciprocal of 27,
\[\begin{align*} 3^{5-2x} &= 27^{-1} \end{align*}\]Express as a base of 3,
\[\begin{align*} 3^{5-2x} &= 3^{-3} \end{align*}\]Then equate its exponents,
\[\begin{align*} 5-2x &= -3 \\ 2x &= 8 \\ x &= 4 \tagans \end{align*}\]$\example{5}$ Solve for $x$, $2^{x^2+x-\frac{11}{2}} = \sqrt{2}$
$\solution$
Express the radical as a power with a rational exponent,
\[\begin{align*} 2^{x^2+x-\frac{11}{2}} &= 2^{1/2} \end{align*}\]Then equate its exponents,
\[\begin{align*} x^2+x-\frac{11}{2} &= \frac{1}{2} \\ 2x^2+2x-11 &= 1 \\ 2x^2+2x-12 &= 0 \\ (2x-4)(x+3) &= 0 \\ (x-2)(x+3) &= 0 \\ \end{align*}\]Hence,
\[\begin{align*} x =2 \quad or \quad x=-3 \tagans \end{align*}\]$\example{6}$ Solve for $x$, $1=\br{ \frac{1}{2} }^{2x+1}$
$\solution$
In this example, we cannot simply match the base of the terms, but remember that any number or variable with an exponent of 0 is equal to 1. And we can use this concept and equate the exponent of $\frac{1}{2}$ to 0. This gives us,
\[\begin{align*} 2x+1 &= 0 \\ 2x &= -1 \\ x &= -\frac{1}{2} \tagans \end{align*}\]Natural Exponential Functions
Natural Exponential Function is a special case of an exponential function, instead of having a base of any constant, it has the Euler’s number $e$ as its base. Natural Exponential Functions is written in the form of,
$$\begin{align} f(x)=e^x \end{align}$$
Where $e$ is a non-terminating irrational number which is approximately $e \approx 2.71828\dots$ Natural Exponential Functions has a lot of applications since the slope at any point on the curve of $y=e^x$ is also equal to $e^x$ (Figure 1). In the subsequent lessons we will see why this function is special.
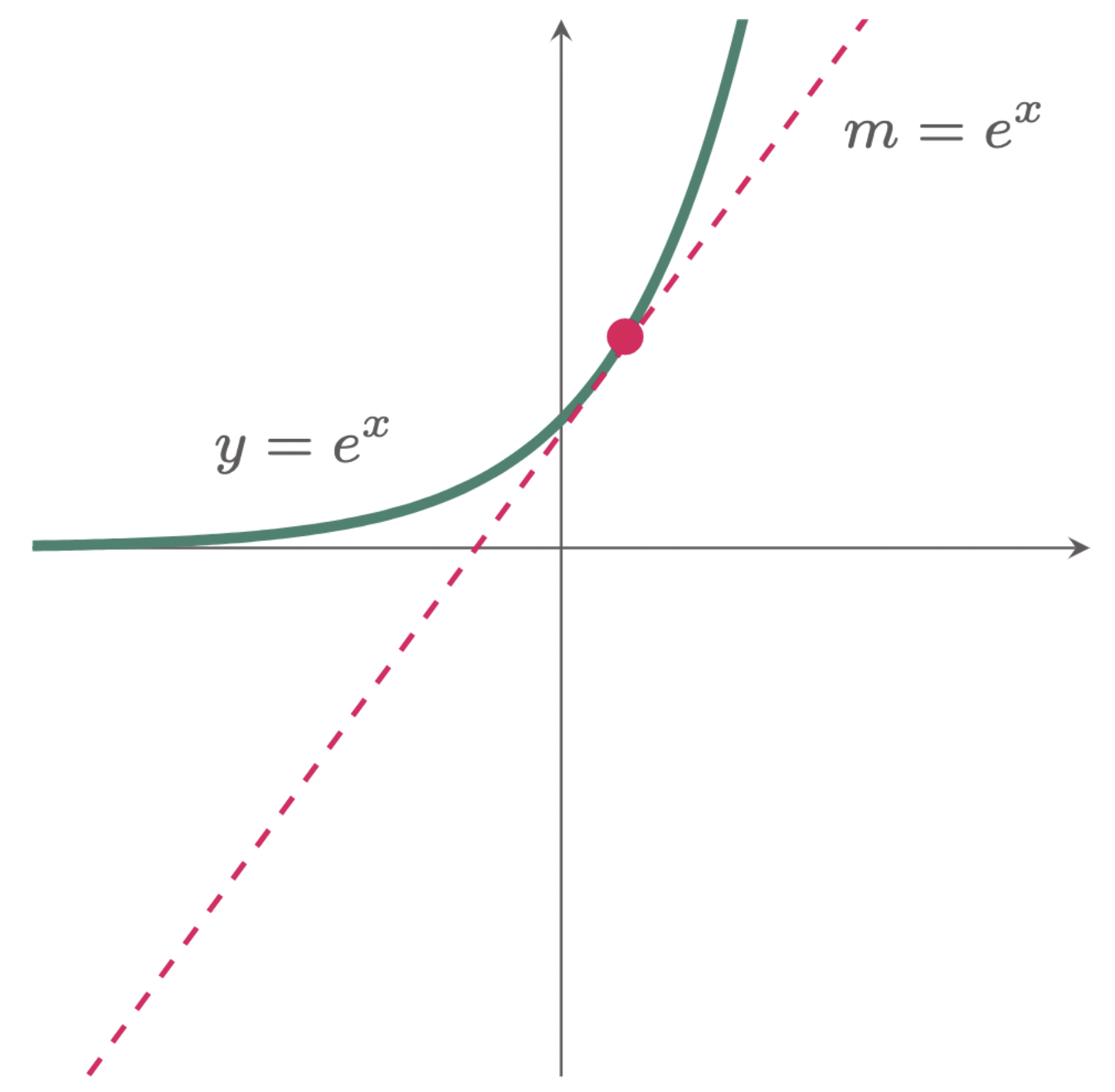
Figure 1: The slope at any point on the curve $y=e^x$ is also equal to $e^x$
$\example{7}$ Solve for $x$, $e^{5x}=e^{7x-3}$
$\solution$
Since the base $e$ is just a constant, we can solve this example by using the same method that we have previously discussed in exponential functions, which is by equating all of its exponents.
\[\begin{align*} 5x &= 7x-3 \\ 2x &= 3 \\ x &= \frac{3}{2} \tagans \end{align*}\]$\example{8}$ Solve for $x$, $e^{2x+3}=1$
$\solution$
From our previous examples, we have learned that in order for the exponents to be equated, its base must be the same. In this case, we want to express both sides with the base $e$. If you recall, any non-zero number raised to the power of zero is equal to 1. Thus, $e^0 = 1$.
\[\begin{align*} e^{2x+3} &= e^0 \end{align*}\]With this in mind, we can equate the exponent $2x+3$ by 0. This gives us,
\[\begin{align*} 2x+3 &= 0 \\ x &= - \frac{3}{2} \tagans \end{align*}\]
