Angle measures the amount of turn between two lines that have a common point, which is called the vertex.
Various symbols can denote Angles, but Greek symbols most frequently represent them. And the most commonly used symbol for an angle is theta, $\theta$.
There are many units that can be used to describe an angle such as degrees, radians, gradians, and mils.
But in calculus, it is more practical to use radians to simplify the calculations, in later chapters we will understand why radians is more desirable to use than other units.
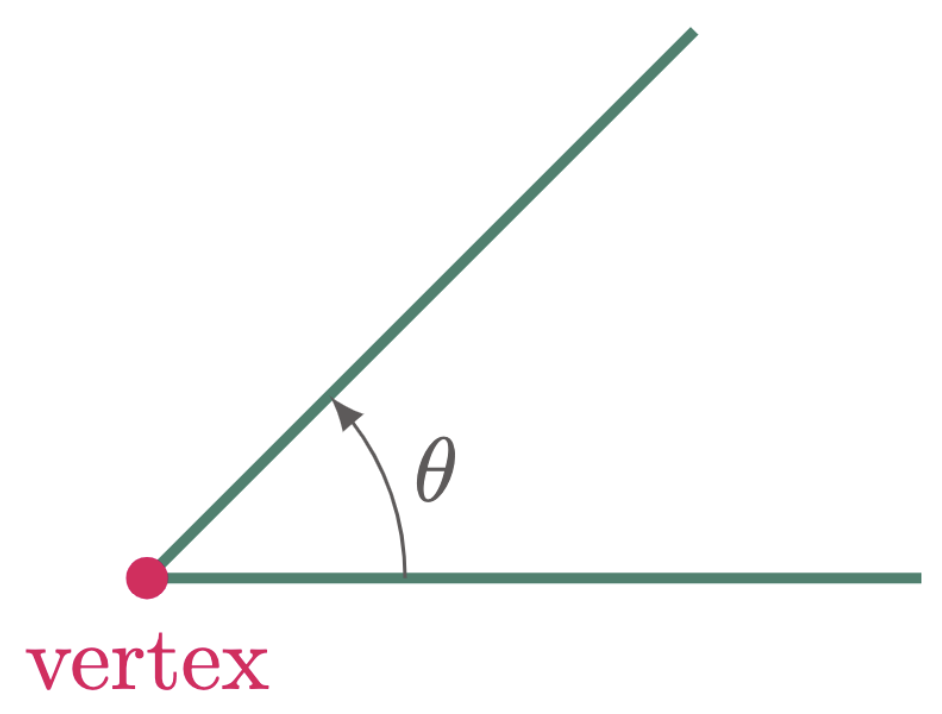
Figure 1: Angle denoted by the greek symbol theta, $\theta$
Radian
Radian is a unit of angle that uses the radius of the circle to describe the angle. To elaborate this, consider $\fref{2}$, if the radius of a circle is laid along its circumference, the angle formed $\theta$ measures to 1 radian.
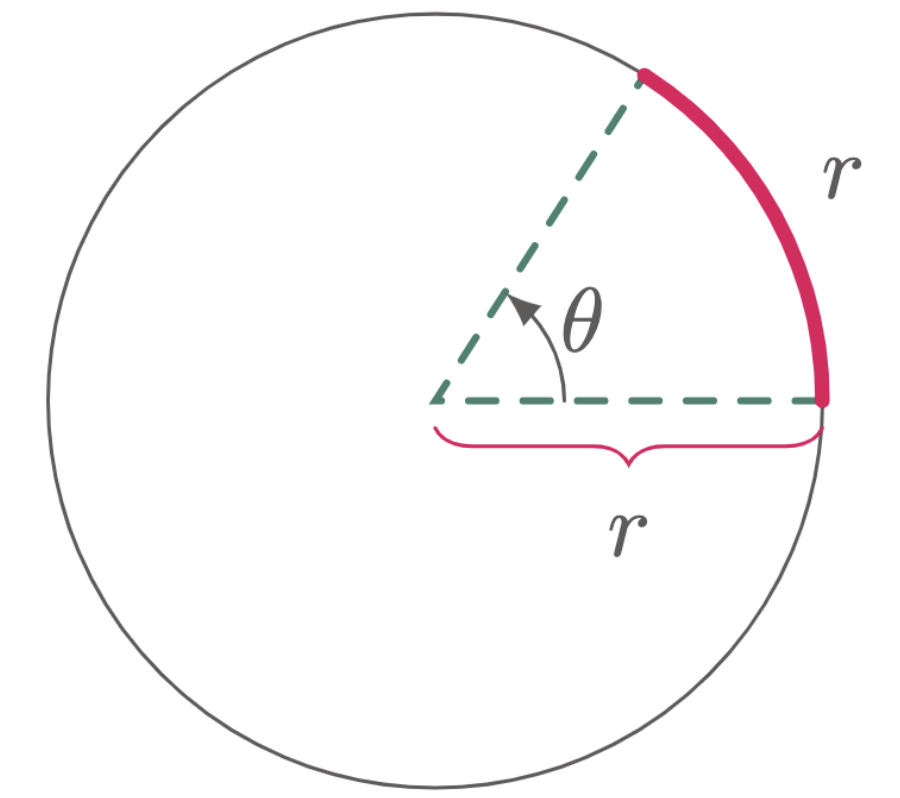
Figure 2: When the length of the arc is equal to the length of the radius, $\theta = 1\un{rad}$
We can also figure out the relationship of radians to other units of angle by fully wraping the circumference of the circle using the length of the radius ($\fref{3}$). Since the circumference of a circle is $C=2\pi r$, then the number of times the radius will be laid to fully wrap the circumference is $2\pi$ times or approximately 6.28 times.
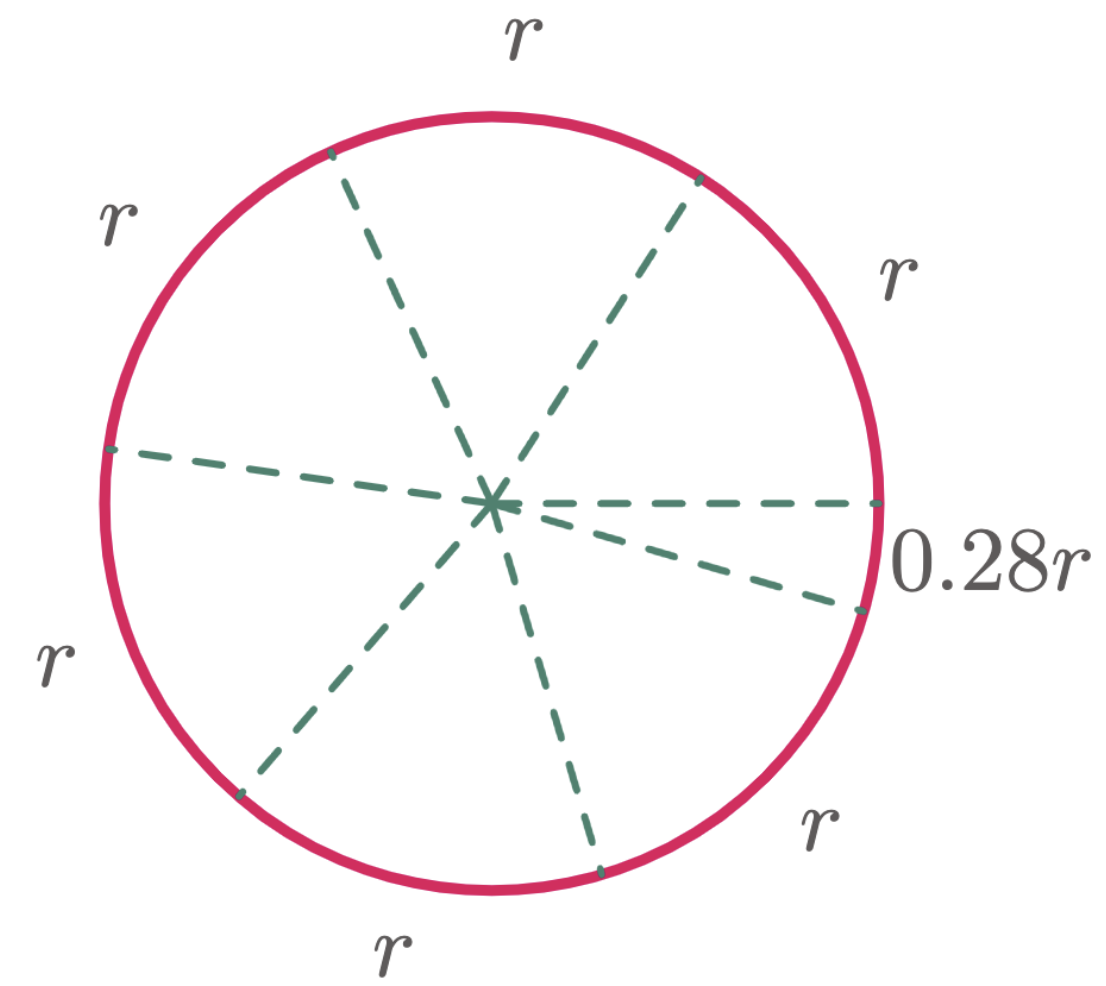
Figure 3: $1\un{revolution} = 2\pi\un{radians}$
Hence, one revolution in terms of radian is $2\pi$ rad.
\[\begin{align*} 1 \un{rev} &= 2\pi \un{rad} \end{align*}\]Since, $360^{\circ}$ is also equal to one revolution,
\[\begin{align*} 1 \un{rev} &= 360^{\circ} \\ 2\pi \un{rad} &= 360^{\circ} \\ 1\un{rad} &= \frac{360\degg}{2\pi} \end{align*}\]$$\begin{align} 1 \un{rad} =\frac{180^{\circ} }{\pi} \end{align}$$
The unit “rad’’ after the angle is usually used to represent a radian, but this is sometimes omitted since radian is the ratio of the length of the arc to its radius, which cancels out the unit resulting to a pure number.

