There are six (6) basic trigonometric functions in trigonometry, namely: sine, cosine, tangent, cosecant, secant, and cotangent. These are abbreviated as: sin, cos, tan, csc, sec, and cot, respectively. Consider $\fref{1}$, the angle $\theta$ on the right triangle shown can be evaluated using these trigonometric functions. Moreover, these functions can be expressed as ratios of the sides of the right triangle.
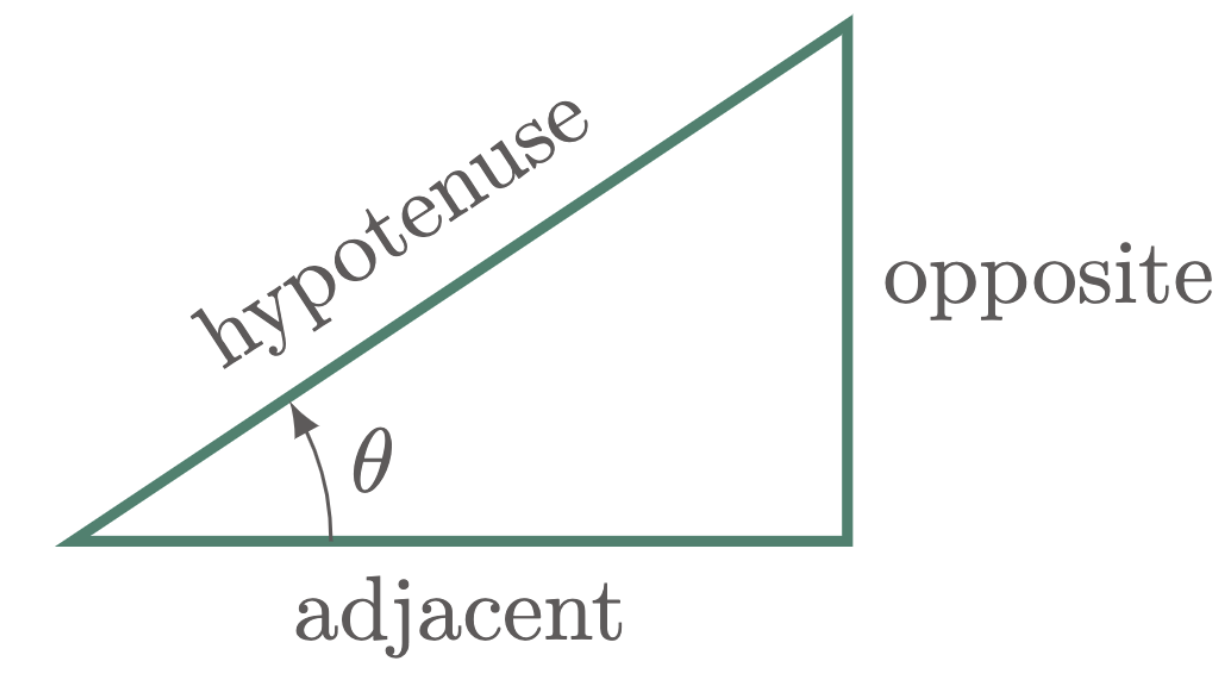
Figure 1: Parts of a right triangle relative to the angle $\theta$
Six Basic Trigonometric Functions
\[\begin{align*} \sin \theta &= \ufrac{opposite}{hypotenuse} = \frac{y}{r} & \csc \theta &= \ufrac{hypotenuse}{opposite} = \frac{r}{y} \\ \cos \theta &= \ufrac{adjacent}{hypotenuse} = \frac{x}{r} & \sec \theta &= \ufrac{hypotenuse}{adjacent} = \frac{r}{x} \\ \tan \theta &= \ufrac{opposite}{adjacent} = \frac{y}{x} & \cot \theta &= \ufrac{adjacent}{opposite} = \frac{x}{y} \\ \end{align*}\]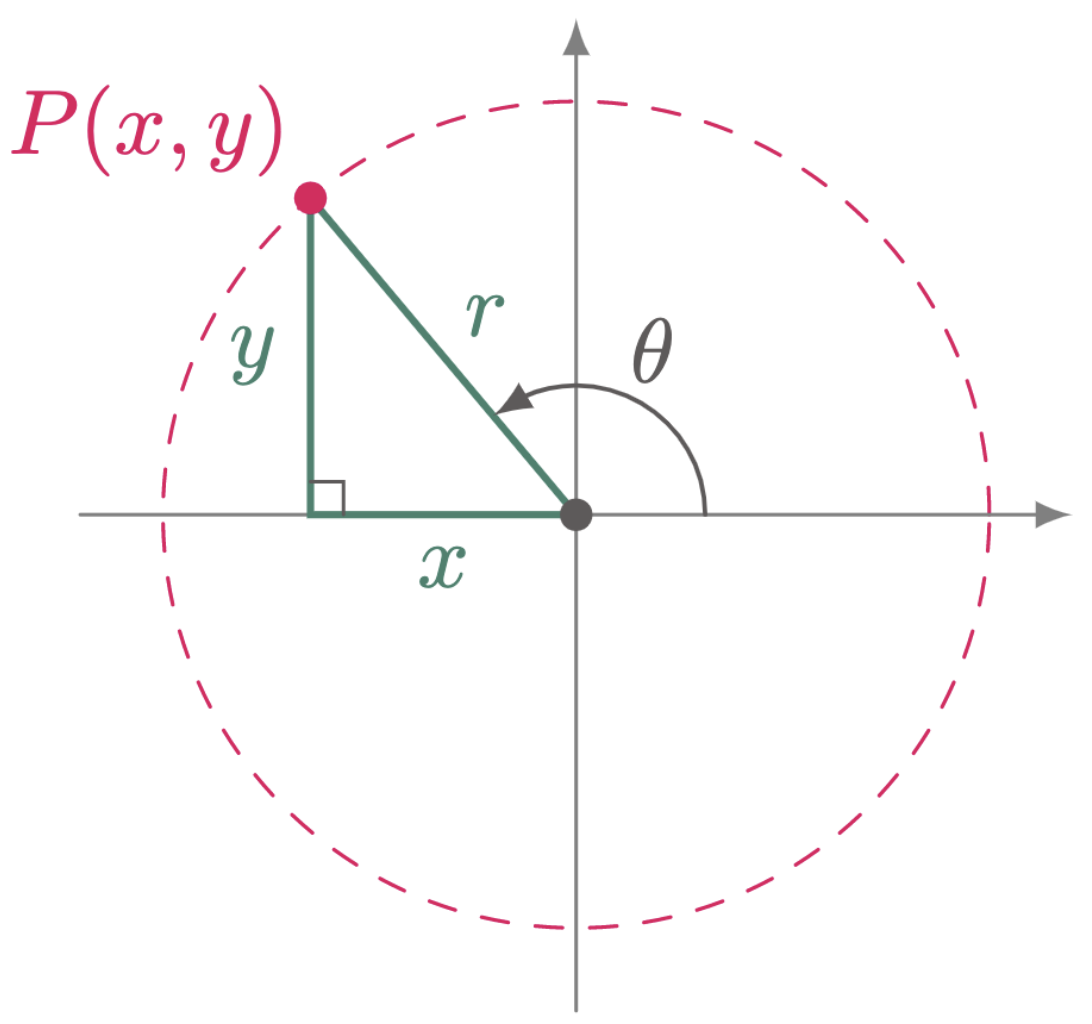
As you may have noticed, $\csc\theta$, $\sec\theta$, and $\cot\theta$ are recipricals of $\sin\theta$, $\cos\theta$, and $\tan\theta$, respectively. Hence, we can also repesent these reciprocal functions as,
$$\begin{align} \csc\theta &= \frac{1}{\sin\theta} \\ \sec\theta &= \frac{1}{\cos\theta} \\ \cot\theta &= \frac{1}{\tan\theta} \end{align}$$
Another notable relationship between these functions is that the tangent and cotangent functions can also be represented in terms of only sine and cosine.
$$\begin{align} \tan\theta &= \frac{\sin\theta}{\cos\theta} \\ \cot\theta &= \frac{\cos\theta}{\sin\theta} \end{align}$$
With these relationships, we can see that all of the trigonometric functions can be represented in terms of only sine and cosine.

