One of the simplest methods in evaluating exact values of trigonometric functions is by using the unit circle. The unit circle is a circle in a cartesian plane with a radius of one and has a center located on the origin. Angles in a unit circle are measured from the positive $x$-axis, with clockwise rotation resulting to a positive angle, and counter-clockwise direction to a negative angle.
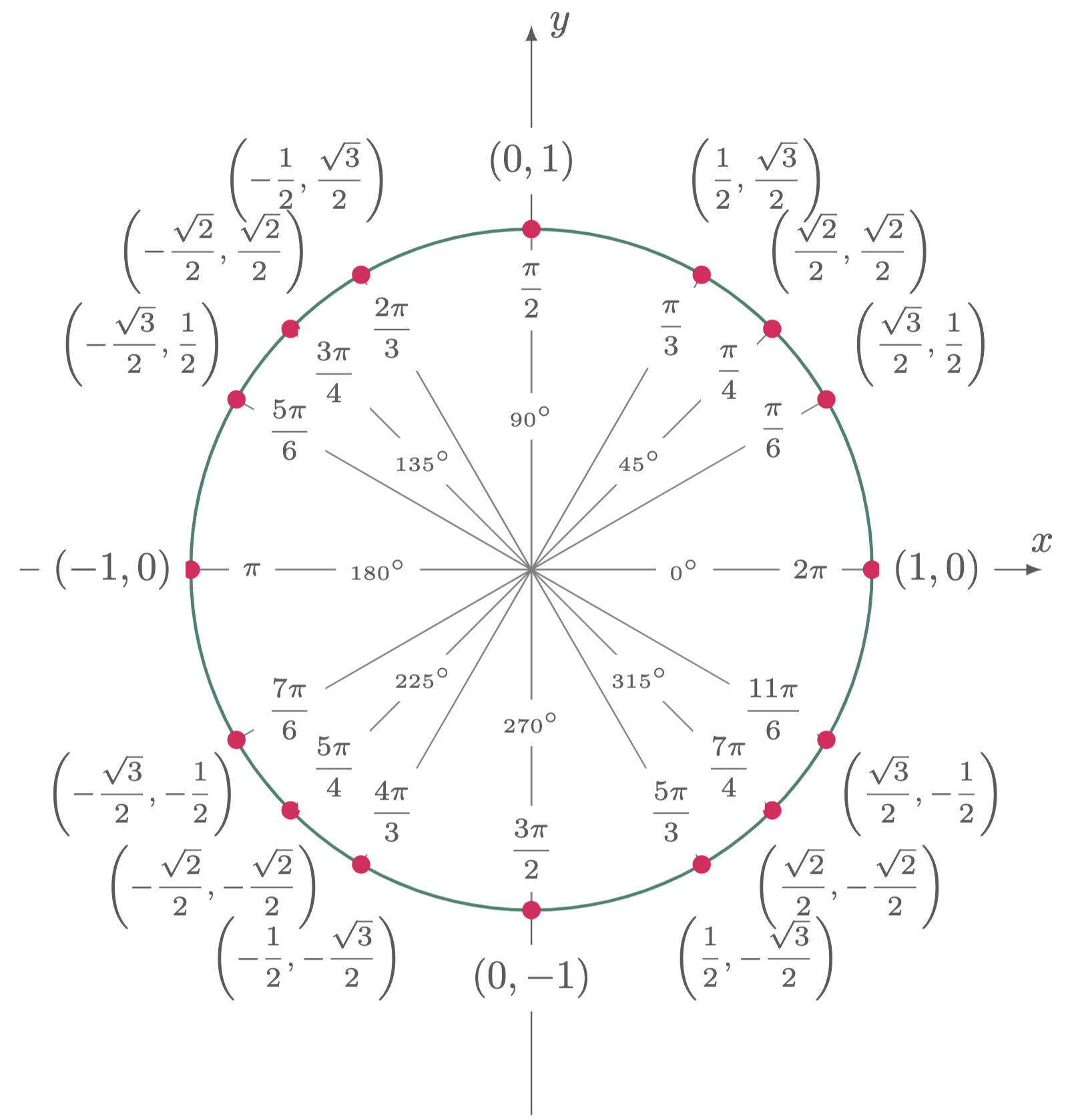
Figure 1: The Unit Circle
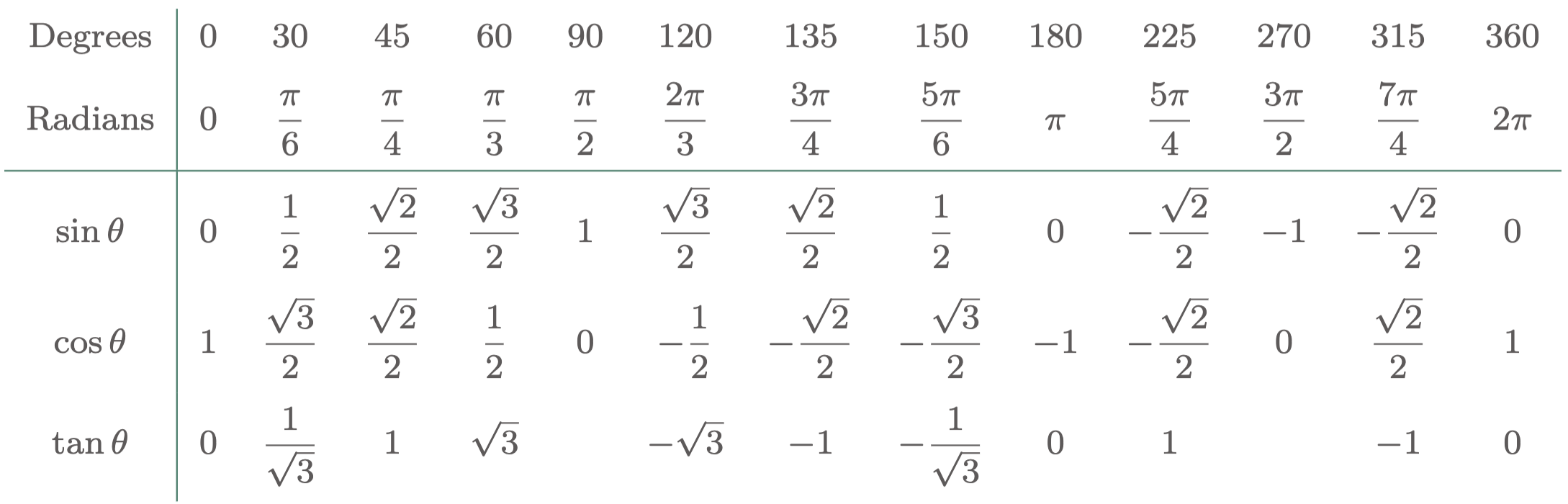
Table 1: Values of trigonometric functions at selected values of $\theta$
For every angle moved in the unit circle there is a corresponding coordinates that lie on its circumference. With this, the formulas for the basic trigonometric functions can be used to evaluate the exact value of such functions.
$\example{1}$ Let $f(\theta) = \sin\theta$, find $f\br{ \frac{3\pi}{2} }$.
$\solution$
\[\begin{align*} f(\theta) &= \sin\theta \\ f\br{\frac{3\pi}{2}} &= \sin\br{\frac{3\pi}{2}} \end{align*}\]
To evaluate the function, use the unit circle or $\tref{1}$,
\[\begin{align*} &= -1 \tagans \end{align*}\]$\example{2}$ Let $f(x) = \csc{x}\tan{x}$, find $f\br{ \frac{5\pi}{6} }$.
$\solution$
\[\begin{align*} f(x) &= \csc{x}\tan{x} \end{align*}\]
Since $\csc{x} = \frac{1}{\sin{x}}$,
\[\begin{align*} &= \frac{1}{\sin{x}} \cdot \tan{x} \\ f\br{\frac{5\pi}{6}} &= \frac{1}{\sin(5\pi/6)} \cdot \tan{\frac{5\pi}{6}} \\ &= \frac{1}{1/2} \cdot \br{-\frac{1}{\sqrt{3}}} \\ &= -\frac{2}{\sqrt{3}} \\ \end{align*}\]To rationalize the denominator, multiply both the numerator and the denominator to $\sqrt{3}$.
\[\begin{align*} &= -\frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}\\ &= -\frac{2\sqrt{3}}{3} \tagans \end{align*}\]
