Integral Calculus is a branch of mathematics concerned with the theory and applications of integrals and integration. Some of its applications are determining areas under a curve, volumes of solids of revolution, and lengths of curves. The integral corresponds to summing infinitesimal pieces to describe the continuous region. In other words, integral calculus is concerned with the process or idea of breaking down into parts to compute the whole. The term “part” is the infinitesimal piece derived from the concept of differentials. As you may have already noticed, Integral Calculus complements the principles of Differential Calculus.
This course is intended for those with an introductory background in Calculus. However, the lectures in this course are written so that anyone who has taken the usual introductory Calculus topics should easily understand the mathematics involved.
Brief History of Integral Calculus
The path to the development of the integral calculus is multi-branched, wherein different people had similar discoveries simultaneously. The beginning of the technique that is currently known as integration can be attributed to the attempts to find the area underneath a curve.
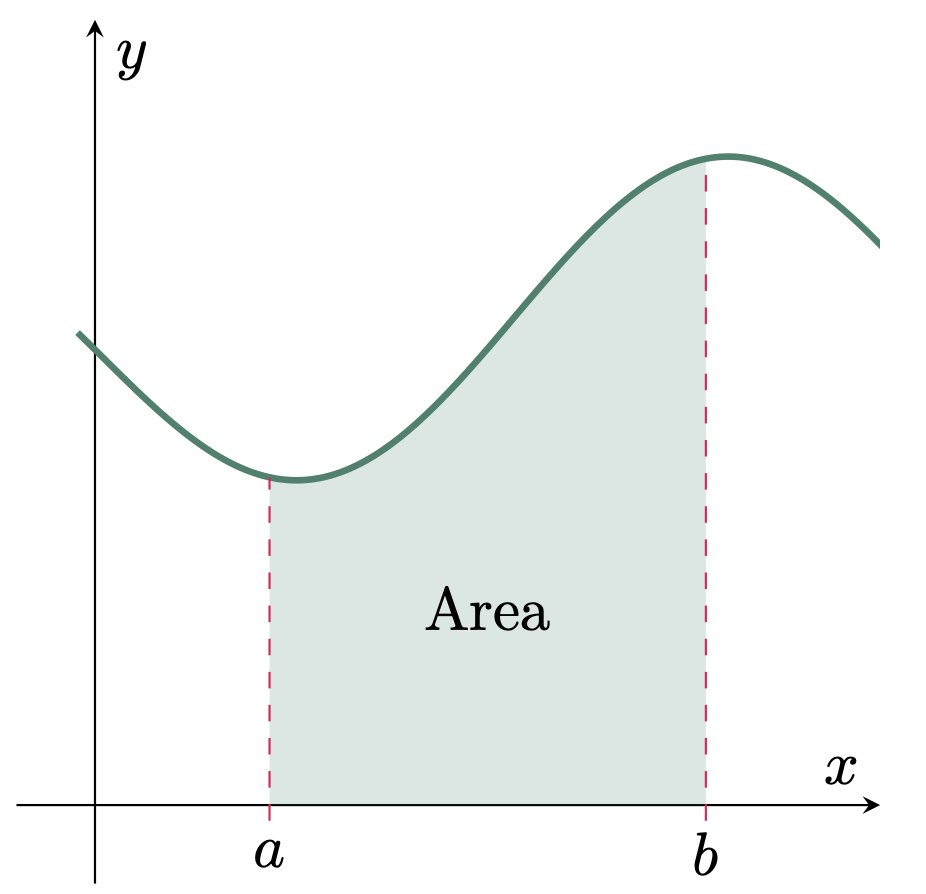
Figure 1: Area under a curve
The foundations for the discovery of the integral were first laid by Cavalieri, an Italian Mathematician, in around 1635. Cavalieri’s work centered around the observation that a curve can be sketched by a moving point. To deal with the geometrical idea of a moving point, Cavalieri worked with what he called “indivisibles.” He theorized that if a moving point can be considered to sketch a curve, then the curve is the sum of its points. By this notion, each curve is made up of an infinite number of points, or the “indivisibles.”
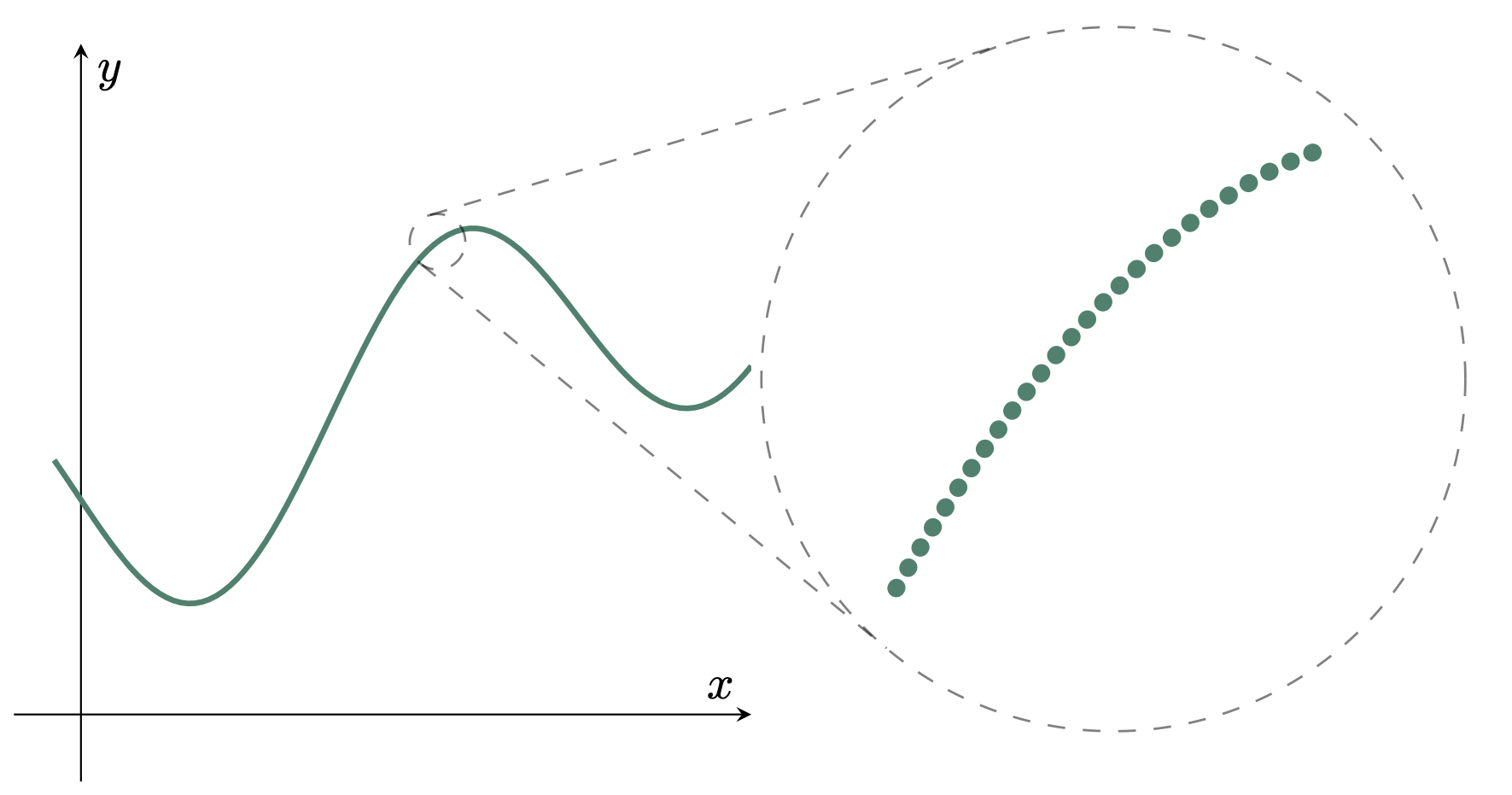
Figure 2: Zoomed partition of a curve
Similarly, an area (regular or irregular shapes) was simply composed of an infinite number of lines.
John Wallis further developed this concept by including the concept of limits and analyzing the behavior of the curves by introducing the idea of an algebraic law for integration that alleviated the necessity of going through tedious analysis for every curve.
One of the first significant uses of infinite series in the development of calculus came from Pierre De Fermat’s method of integration. Though both Cavalieri and Wallis’ methods of integration had used the notion of infinite lines describing an area, Fermat was the first to use infinite series in his methodology. The first step in his method involved a unique way of describing the infinite rectangles making up the area under a curve. This method was widely used and became the foundation of the techniques used to this day.
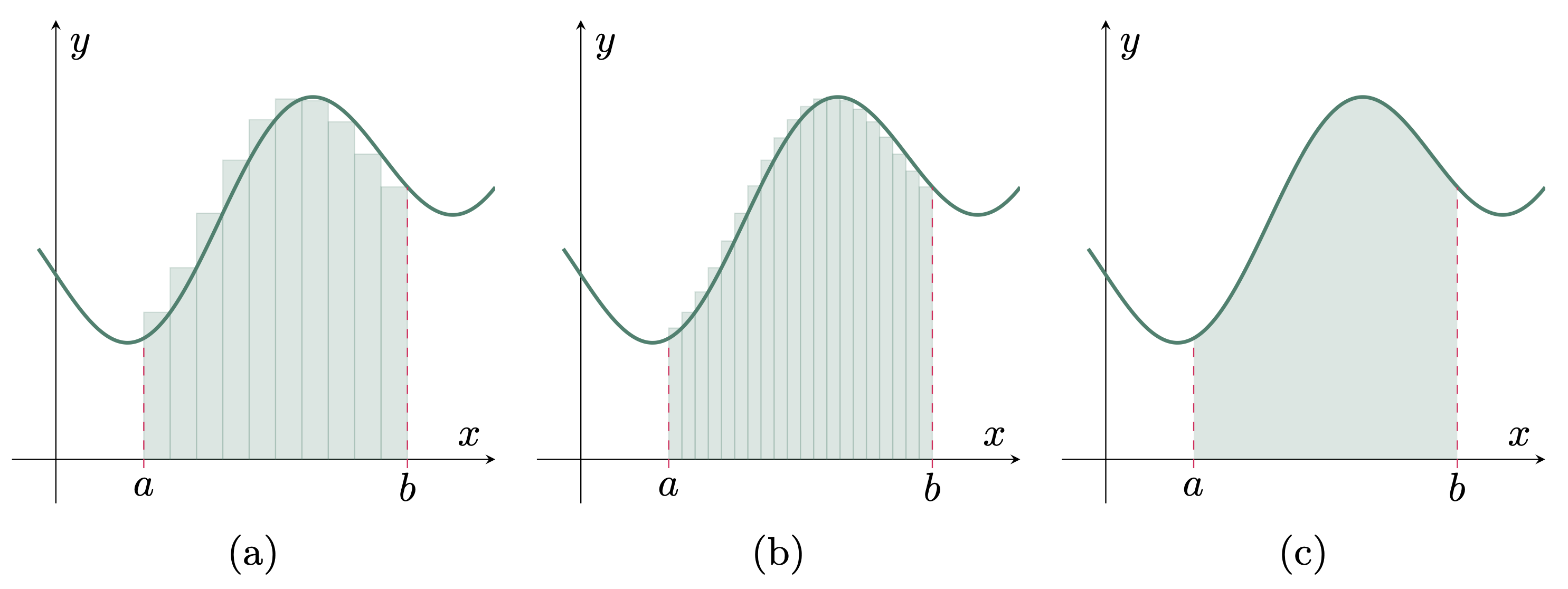
Figure 3: Increasing the number of rectangles infinitely to increase the accuracy of approximation of the area under the curve
The present-day calculus was introduced during the mid-17th Century by both Sir Isaac Newton and Gottfried Wilhelm Leibniz. It is now believed that both men discovered the calculus independent of each other. However, records show that Newton discovered it eight years earlier than Leibniz. One of the trivia’s worth noting is that Newton discovered calculus at the age of 22.
In this course, it is now our turn to re-discover integral calculus and learn its importance and application in the engineering and technology field. We will begin our adventure by exploring the concept of integration which is also called anti-derivatives.

