Integral Calculus has a lot of applications, but having no prior knowledge of what it really is, grasping its concepts can be a little overwhelming. To start, let us first understand where the equation for the area of a circle comes from. $A = \pi r^2$, what really is $\pi$? and why $r^2$? If you come to think of it, $r^2$ is an area of a square with a side that has a length of $r$. And $\pi$ is simply the ratio of the circumference of the circle to its diameter $\pi = \frac{C}{d}$, it is equivalent to approximately 3.14 (see Figure 1). Keeping this in mind, we can easily determine the circumference of a circle $C$ using only its diameter $d$ ($C=\pi d$).

Figure 1: Relationship of $\pi$ with the circle’s circumference and radius
Areas of simple figures such as a square, a rectangle, or a triangle can be easily verified by simple logic. Take the area of a square or a rectangle, for instance; if you are in a classroom and the chairs are perfectly arranged in a grid-like structure, we can easily figure out the number of chairs by multiplying the number of rows and columns. With this in mind, the area can be represented by the total number of chairs in the room; it is simply length times width ($A=lw$).
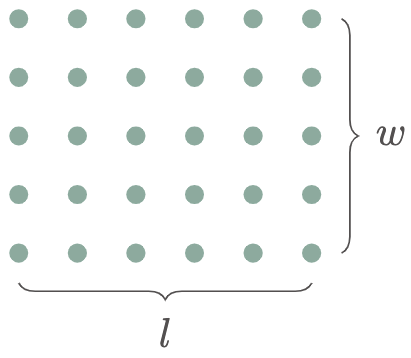
Figure 2: Relating the area of a rectangle with the total number of dots
Moreover, triangles are just rectangles split in half. So, figuring out the equation of the area of a triangle is not surprising; all you need to do is divide the area of the rectangle in half.
\[\begin{align*} A_\text{tri} &= \frac{A_\text{rec}}{2} \\ A_\text{tri} &= \frac12 bh \end{align*}\]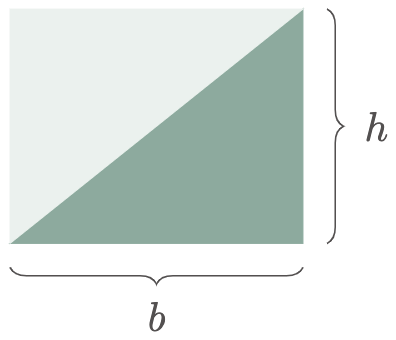
Figure 3: Area of a triangle is half the area of a rectangle
The area of the circle, on the other hand, is not that straightforward to figure out. To understand, let us start with a circle and cut it into concentric rings. Imagine that the circle, or the rings in particular, are made of a material that can be bent. If we cut from the center of the circle to the outermost ring, we can unroll the rings into strips of rectangles.
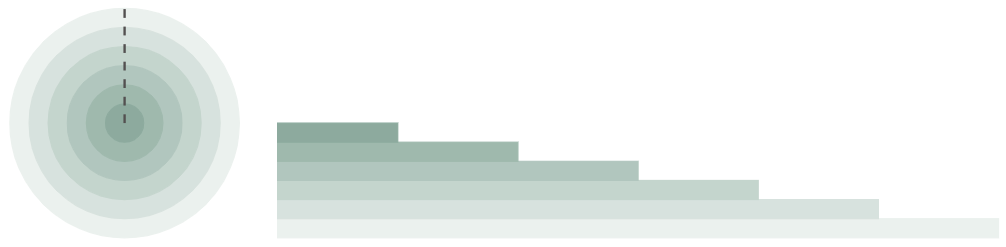
Figure 4: Unrolling the rings into rectangular strips
Placing the strips side by side in an ascending order reveals a different shape: a shape that we already know how to solve, a simple right triangle. Furthermore, we can make the thickness of the rings thinner to refine the shape further.

Figure 5: Increasing the number of rectangles to increase the accuracy of approximation of the area
You might have already figured it out, the height of the triangle resembles the circle’s radius and the base as the circumference.
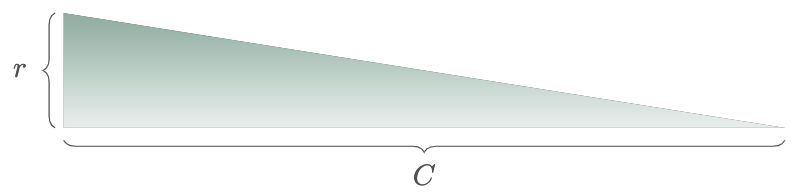
Figure 6: Relationship of the parts of the formed triangle to the circle
Applying the equation of the triangle gives us,
\[\begin{align*} A &= \frac12 bh \\ A &= \frac12 Cr \end{align*}\]But $C=\pi d$,
\[\begin{align*} &= \frac12 (\pi d)r \end{align*}\]And we can also represent the diameter $d$ in terms of the circle’s radius, $d=2r$
\[\begin{align*} &= \frac12 (2\pi r)r \\ &= \frac{1}{\cancel{2}} (\cancel{2}\pi r^2) \\ A &= \pi r^2 \end{align*}\]This is only one of the many ways the formula of the area can be derived, there are numerous methods with different underlying concepts, all we need is a little imagination.
Understanding the concepts on how formulas have been derived gives us a better understanding and appreciation of this kind of topic.
The core concept of integral calculus is taking the sum of infinitely small quantities to be represented as a whole. Its primary goal is simple and is equipped with some essential mathematical tools. As a result, problems that were once impossible to solve can now be easily manipulated using calculus.

