Before proceeding with our topic, it is essential to understand the basic rules and laws governing exponential and logarithmic functions. It is also crucial to appreciate the importance of these functions in many real-world applications. Exponential and logarithmic functions are present in various fields, specifically in modelling population growth, cell growth and decay, financial growth and depreciation, and radioactive decay, to name a few of its applications. Nevertheless, you can review some of the fundamental laws and concepts underlying these functions to understand this topic better.

In this lesson, we will learn how to integrate both exponential and logarithmic functions. However, before we can proceed, it is best to review the methods of differentiating these functions. Considering that integration is the inverse of differentiation; thus, understanding the relationship between the two methods is ideal for us to have a deeper appreciation of this topic.

Integration Formulas for Exponential and Logarithmic Functions

For the following formulas in evaluating indefinite integrals, let $u$ be a function of $x$; $a$ as a constant; $e$ as the Euler’s number; and $C$ as the constant of integration.

$$\begin{align} \int \frac{du}{u} &= \ln|u|+C \qquad\text{where: } u>0 \label{eq:integral of Natural Logarithmic Function} \\ \int e^u\,du &= e^u+C \label{eq:integral of Exponential Function e^u}\\ \int a^u\,du &= \frac{a^u}{\ln a}+C \label{eq:integral of Exponential Function a^u} \end{align}$$

---

$\example{1}$ Evaluate the integral $\int \frac{x}{x^2+1}\,dx$

$\solution$
Let: $\tcA{u = x^2+1}$

Differentiating the function gives us,

$$\begin{align*} d(u) &= d(x^2+1) \\ du &= 2x\,dx \\ \tcB{\frac{du}{2}} & \tcB{= x\,dx } \end{align*}$$

Then rearrange the given integral,

$$\begin{align*} \int \frac{x}{x^2+1}\,dx &= \int\frac{x\,dx}{x^2+1} \\ &= \int\frac{\tcB{du/2}}{\tcA{u}} \\ &= \frac12\int\frac{du}{u} \\ \end{align*}$$

As you can recall in our previous lesson, we cannot use the General Power Rule for Integration if $n = -1$, as you may have realized that this problem is a solution to that restriction. Since $\int \frac{du}{u}$ is just equal to $\int u^{-1}\,du$. We can now solve this problem using $\eref{eq:integral of Natural Logarithmic Function}$. Thus,

$$\begin{align*} \int \frac{x}{x^2+1}\,dx &= \frac12 \ln|u|+C \end{align*}$$

Since, $u = x^2+1$

$$\begin{align*} \int \frac{x}{x^2+1}\,dx &= \frac12\ln|x^2+1|+C \tagans \end{align*}$$

---

$\example{2}$ Evaluate the integral $\int \frac{x^3-4x^2+x-3}{x+2}\,dx$

$\solution$
In this case, the integrand is an improper fraction since the numerator’s degree is greater than the denominator. To simplify the rational function, we can first divide the numerator by the denominator.

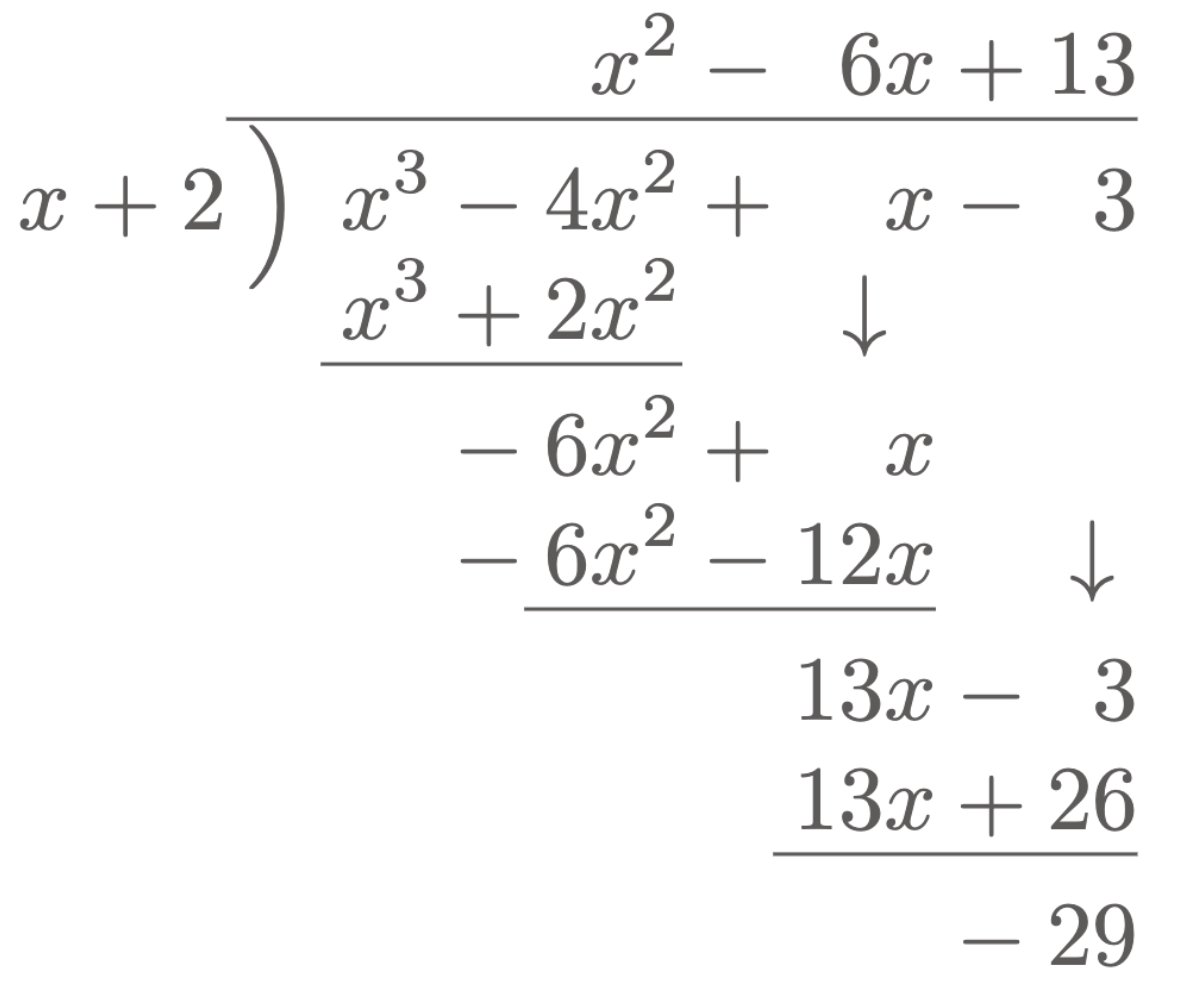
Dividing the rational function results to $x^2-6x+13$ with a remainder of $-29$. Hence,

$$\begin{align*} \int\frac{x^3-4x^2+x-3}{x+2}\,dx &= \int\br{x^2-6x+13-\frac{29}{x+2} }\,dx \\ &= \int x^2\,dx - 6\int x\,dx + 13\int\,dx - 29\int\frac{dx}{x+2} \\ &= \frac{x^3}{3}-\frac{6x^2}{2}+13x-29\ln|x+2|+C \\ &= \frac13 x^3-3x^2+13x-29\ln|x+2|+C \tagans \end{align*}$$

---

$\example{3}$ Evaluate the integral $\int e^{2x-7}\,dx$

$\solution$
$\begin{align*} \text{Let:}\quad u &= 2x-7 & \\ du &= 2\,dx \\ \frac12\,du &= dx \end{align*}$

Express the function in terms of $u$. Then to integrate the function, use $\eref{eq:integral of Exponential Function e^u}$,

$$\begin{align*} \int e^{2x-7}\,dx &= \int e^u \cdot\frac12\,du \\ &= \frac12 \int e^u\,du \\ &= \frac12 e^u+C \end{align*}$$

Since, $u = 2x-7$

$$\begin{align*} \int e^{2x-7}\,dx &= \frac12 e^{2x-7}+C \tagans \end{align*}$$

---

$\example{4}$ Evaluate the integral $\int \frac{3e^{1/x}}{x^2}\,dx$

$\solution$
$\begin{align*} \text{Let:}\quad u &= 1/x & \\ du &= d(x^{-1}) \\ &= -x^{-2}\,dx \\ &= -\frac{1}{x^2}\,dx \\ -du &= \frac{dx}{x^2} \end{align*}$

Express the function in terms of $u$. Then to integrate the function, use $\eref{eq:integral of Exponential Function e^u}$,

$$\begin{align*} \int \frac{3e^{1/x}}{x^2}\,dx &= 3\int e^{1/x}\cdot\frac{dx}{x^2} \\ &= 3\int e^u (-du) \\ &= -3\int e^u \,du \\ &= -3 e^u+C \end{align*}$$

Since, $u = 1/x$

$$\begin{align*} \int \frac{3e^{1/x}}{x^2}\,dx &= -3e^{1/x}+C \tagans \end{align*}$$

---

$\example{5}$ Evaluate the integral $\int \frac{dx}{e^{3x}+1}$

$\solution$
In this case, we cannot directly use the formula for integrating an exponential function. But by adding $e^{3x}-e^{3x}$ to the numerator, the integral can be broken down into two rational functions while still retaining its original value since $e^{3x}-e^{3x}$ is just equal to zero.

$$\begin{align*} \int \frac{dx}{e^{3x}+1} &= \int\frac{1+e^{3x}-e^{3x}}{e^{3x}+1} \\ &= \int\frac{\cancel{1+e^{3x}}}{\cancel{1+e^{3x}}}\,dx - \int\frac{e^{3x}}{e^{3x}+1}\,dx \\ &= \int\,dx-\int\frac{e^{3x}}{e^{3x}+1}\,dx \\ &= x - \frac13\int\frac{3e^{3x}}{e^{3x}+1}\,dx \\ &= x - \frac13\ln|e^{3x}+1|+C \tagans \end{align*}$$

---

$\example{6}$ Evaluate the integral $\int 3^{2x}\,dx$.

$\solution$
$\begin{align*} \text{Let:}\quad a &= 3 & \\ u &= 2x \\ du &= 2\,dx \\ \frac{du}{2} &= dx \end{align*}$

Express the function in terms of $u$. Then to integrate the function, use $\eref{eq:integral of Exponential Function a^u}$,

$$\begin{align*} \int 3^{2x}\,dx&= \int a^2 \cdot\frac{du}{2} \\ &= \frac12 \int a^u\,du \\ &= \frac12 \cdot \frac{a^u}{\ln a}+C \\ &= \frac12\cdot \frac{3^{2x}}{\ln 3}+C \\ &= \frac{9^x}{2\ln 3}+C \tagans \end{align*}$$

---

Related Articles

• Exponential Functions
• Logarithmic Functions
• Derivatives of Exponential and Logarithmic Functions