Integration by parts may be daunting at first, especially it is comprised of different types of functions. Moreover, there are instances in evaluating integrals by integration by parts that there is a need to perform the process more than once. There are already available methods that don’t require this rigorous process anymore, hence evaluating integrals with such method can be further simplified.
The method that we will cover in this lesson is Tabular Integration by Parts, where we will tabulate the derivative of one function and the integral of the other repetitively. In order for us to make a good use of this method, let us have several examples that will show the different possible cases.
$\case{I}$ The $u$ column reduces to zero “$0$’’
$\example{1}$
Evaluate the integral $\int x^2 \sin 2x\,dx$
$\solution$
In this method, we can still use the acronym LIATE in choosing the $u$ and $dv$ of the integrand. Since $x^2$ is an algebraic function and $\sin x$ is a trigonometric function,
\(\begin{align*}
\text{Let:}\qquad u &= x^2 & dv &= \sin 2x\,dx &&&&&&&
\end{align*}\)
In evaluating the integrals using the tabular method, create a column for $u$ and another for $dv$. In the $u$ column, differentiate the function, then write its derivative below it. Similarly, in the $dv$ column, instead of differentiation, integrate the function, then continue the process.

When the $\tcBal{$u$ column reduces to zero “$0$”}$, stop the process. And to evaluate the integral, multiply each $u$ with the $dv$ diagonal lower from it bearing an alternating sign starting with positive ($+$).
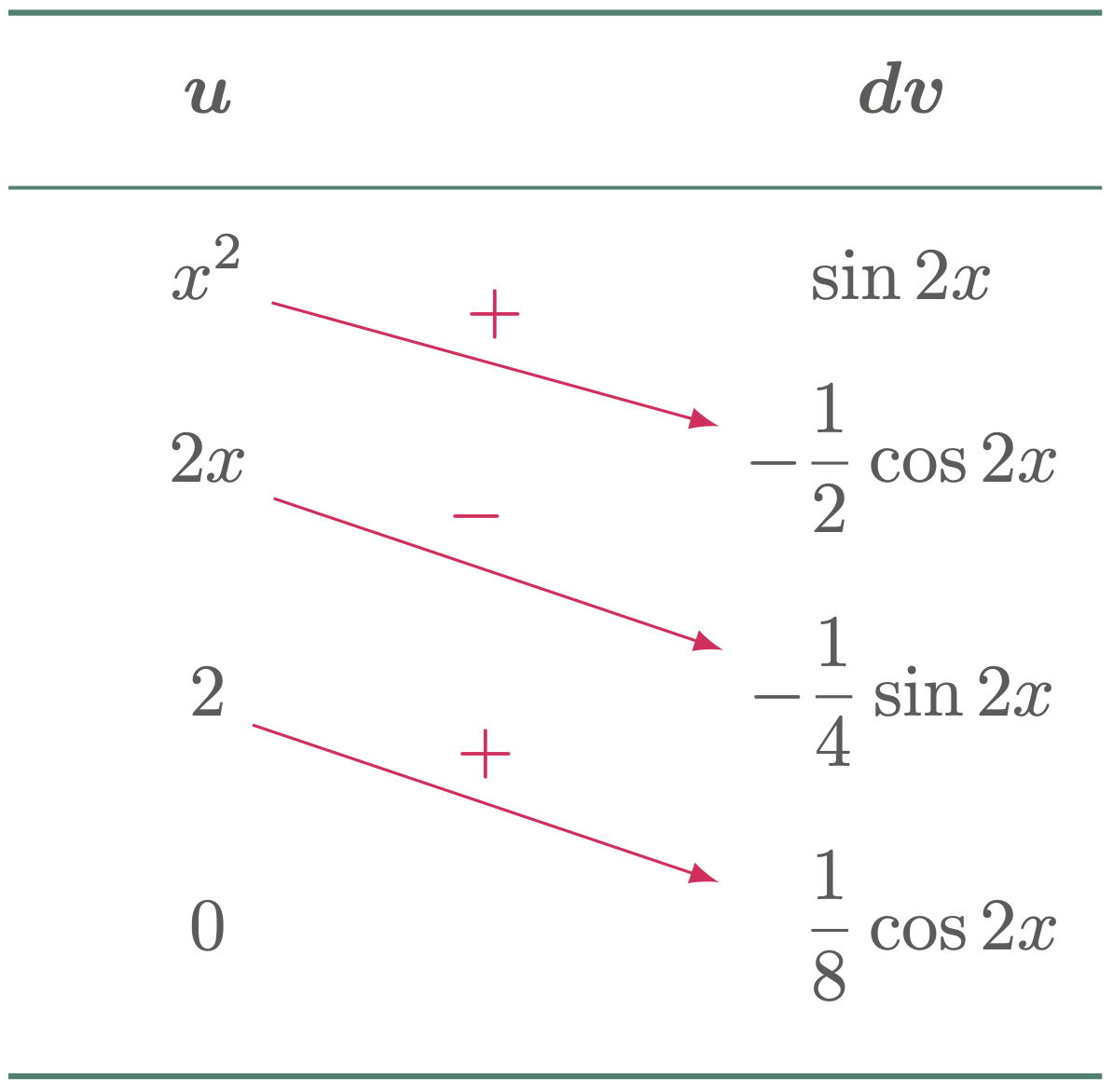
Therefore,
\[\begin{align*} \int x^2 \sin 2x\,dx &= x^2\br{-\frac12\cos2x}-2x\br{-\frac14\sin2x}+2\br{\frac18\cos2x}+C \\ &= -\frac12 x^2\cos2x+\frac12x\sin2x+\frac14\cos2x+C \tagans \end{align*}\]$\case{II}$ The product of the last row can be easily integrated
$\example{2}$
Evaluate the integral $\int x^3\ln x\,dx$
$\solution$
Since $\ln x$ is a logarithmic function and $x^3$ is an algebraic function,
\(\begin{align*}
\text{Let:}\qquad u &= \ln{x} & dv &= x^3\,dx &&&&&&&
\end{align*}\)
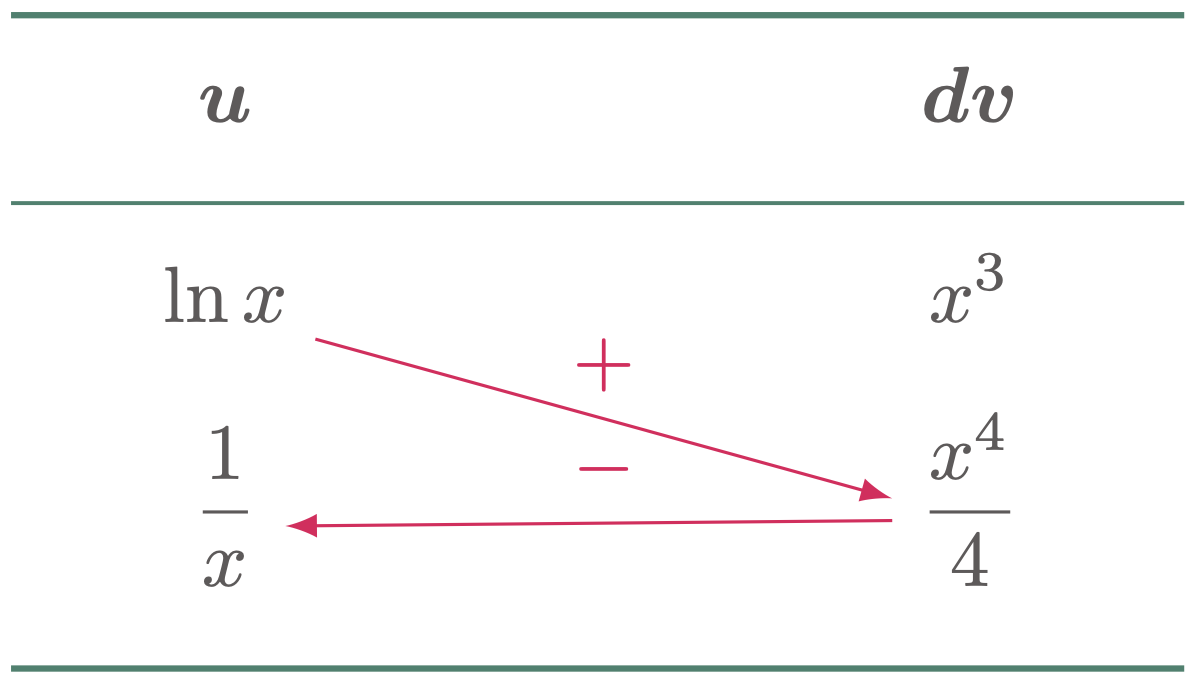
In instances where the $u$-column does not end up reducing to zero, but the product of the last row can already be easily integrated, the same solution as the first case can be used together with an additional step which is adding the integral of the product of the last row.
\[\begin{align*} \int x^3\ln x\,dx &= \ln{x}\cdot\frac{x^4}{4}-\int \frac{x^4}{4}\cdot\frac{1}{x}\,dx \\ &= \frac{x^4}{4} \ln{x}-\frac14\int x^3\,dx \\ &= \frac{x^4}{4} \ln{x}-\frac14\cdot\frac{x^4}{4}+C \\ &= \frac{x^4}{4} \ln{x}-\frac{x^4}{16}+C \tagans \end{align*}\]$\case{III}$ The original integral appears again
$\example{3}$
Evaluate the integral $\int e^{2x}\sin 3x\,dx$
$\solution$
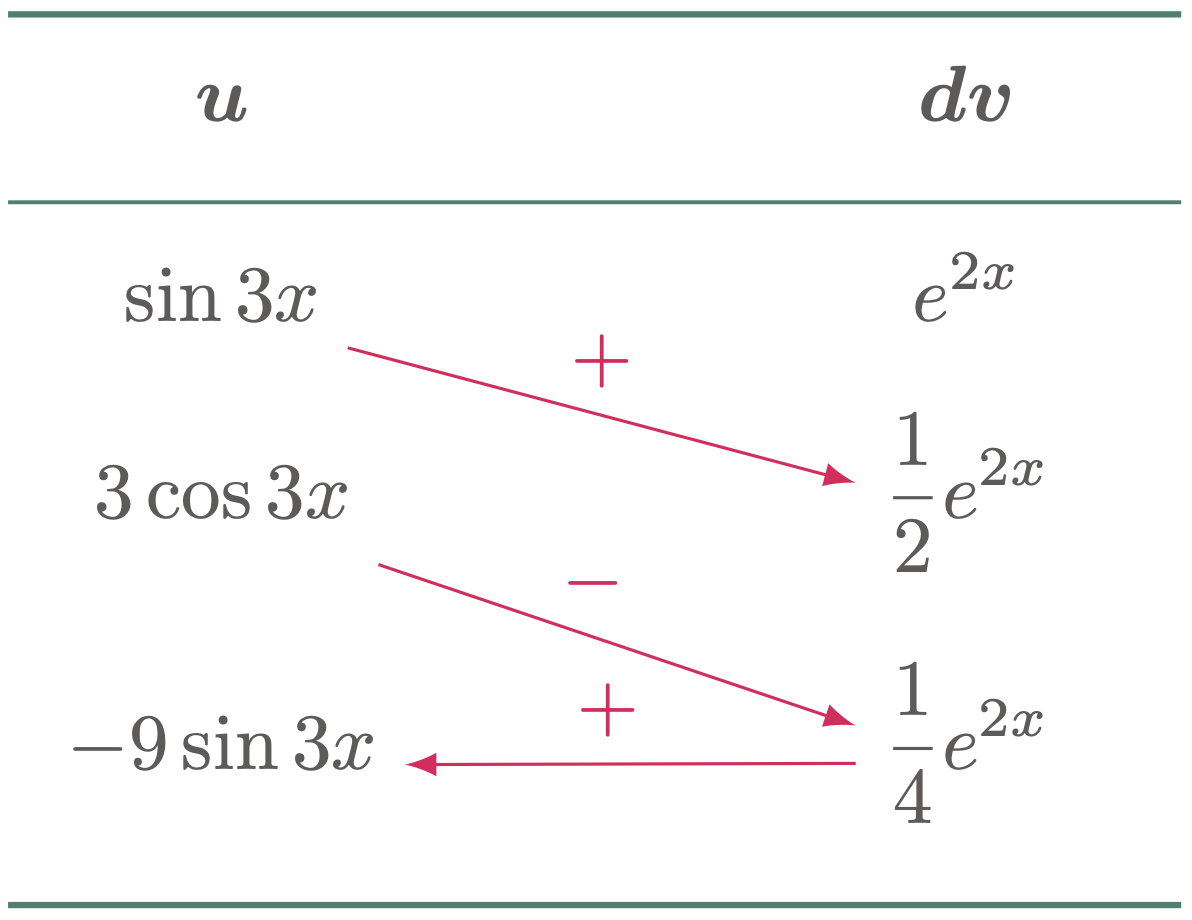
For this case, the original integral appears again, containing a different coefficient. This can be solved using the same solution as the second case.
\[\begin{align*} \int e^{2x}\sin 3x\,dx &= \frac12 e^{2x}\sin{3x}-\frac34 e^{2x}\cos{3x} + \frac94 \int e^{2x}(-\sin 3x)\,dx \\ &= \frac12 e^{2x}\sin{3x}-\frac34 e^{2x}\cos{3x} - \frac94 \int e^{2x}\sin 3x\,dx \\ \int e^{2x}\sin 3x\,dx + \frac94 \int e^{2x}\sin 3x\,dx &= \frac12 e^{2x}\sin{3x}-\frac34 e^{2x}\cos{3x} + C \\ \frac{13}{4} \int e^{2x}\sin 3x\,dx &= \frac12 e^{2x}\sin{3x}-\frac34 e^{2x}\cos{3x} + C \\ \int e^{2x}\sin 3x\,dx &= \frac{4}{13} \br{\frac12 e^{2x}\sin{3x}-\frac34 e^{2x}\cos{3x}} + C \\ &= \frac{1}{13} \br{2e^{2x}\sin{3x}-3 e^{2x}\cos{3x}} + C \tagans \end{align*}\]$\case{IV}$ Rows can be simplified
$\example{4}$
Evaluate the integral $\int \ln^2x\,dx$
Evaluating integrals using the tabulation method sometimes may lead to a row that can be simplified. If this happens, we can rewrite the simplified functions to the next row, and a horizontal broken line can also be added to emphasize where the simplification occurs.
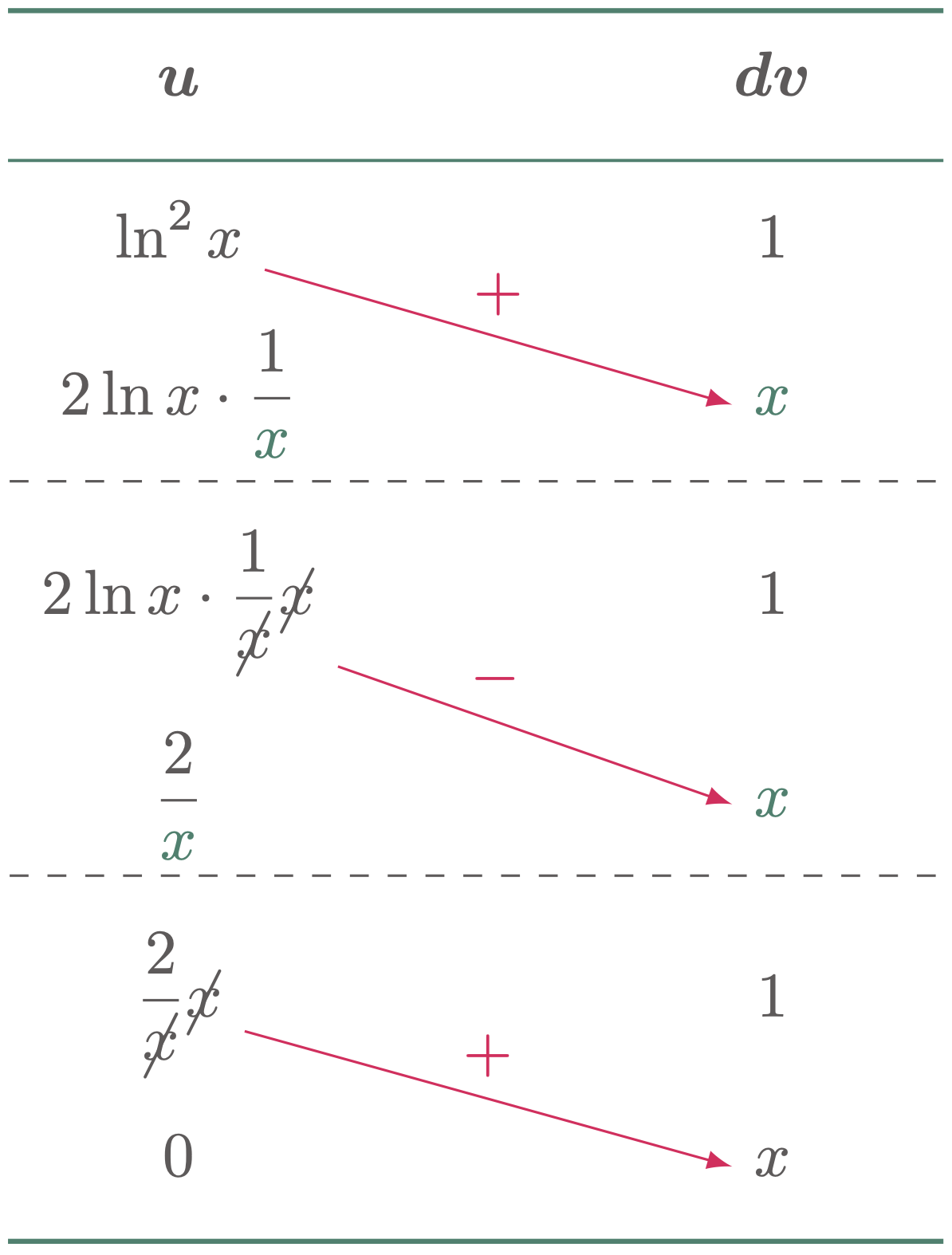
Hence,
\[\begin{align*} \int \ln^2 x \,dx = x\ln^2 x - 2x\ln x + 2x + C \tagans \end{align*}\]$\case{V}$ Rows can be redistributed
$\example{5}$
Evaluate the integral $\int x^3e^{x^2}\,dx$
In cases where simplification may not be enough, we can also redistribute variables to another column in a row. A horizontal broken line can also be added to emphasize where the redistribution occurs.
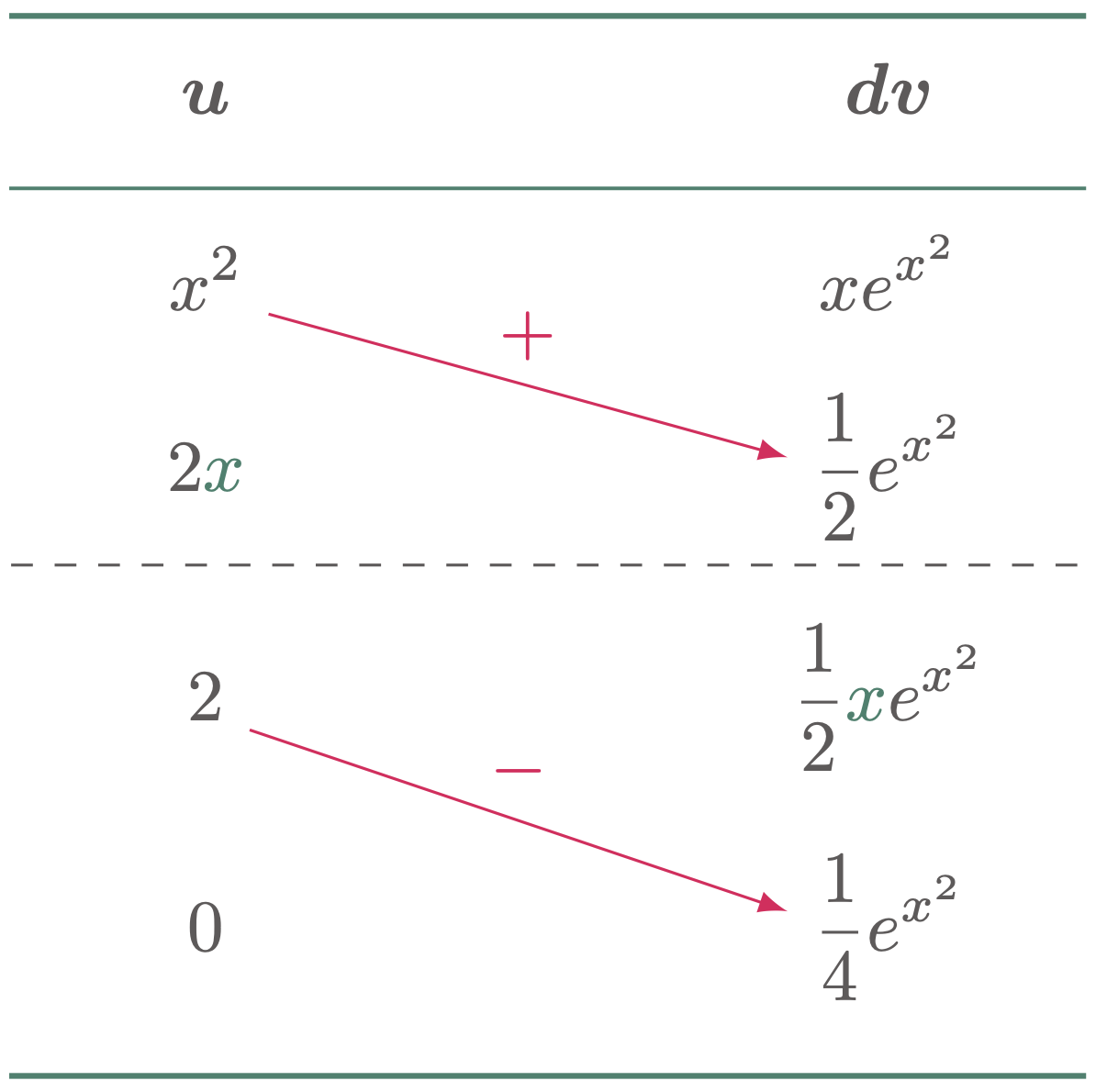
Hence,
\[\begin{align*} \int x^3e^{x^2} \,dx &= \frac{1}{2}x^2e^{2x} -{2 \cdot \frac{1}{4}}e^{x^2} + C \\ &= \frac{1}{2}x^2e^{2x} - \frac{1}{2}e^{x^2} + C \tagans \end{align*}\]
