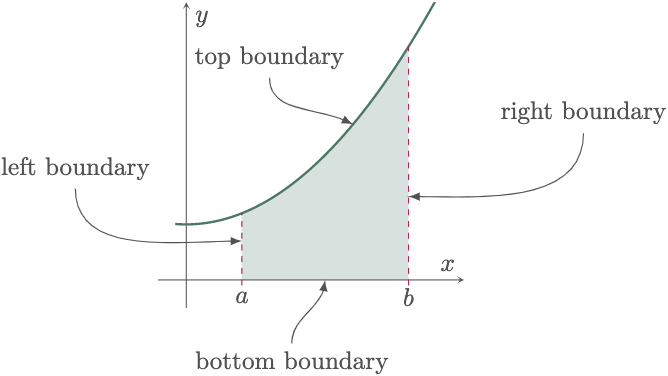
From the previous lesson, we have already discussed definite integrals, as well as visualize its relation in plane areas. However, we have only scratched the surface of plane areas using integration. In this lesson, we will explore some of the methods in solving for the area under a curve. To start, we must first establish that before we can solve for the area, its boundaries must be defined by an equation or by a point of intersection of curves.
If we can recall from analytic geometry, lines in a Cartesian Plane even horizontal and vertical lines, can be expressed as an equation ($\fref{1}$). With this in mind, the $x$ and $y$ axis can also be expressed as an equation since these two are also horizontal and vertical lines respectively ($\fref{2}$), where the $x$-axis can be denoted by $y=0$ and the $y$-axis as $x=0$.
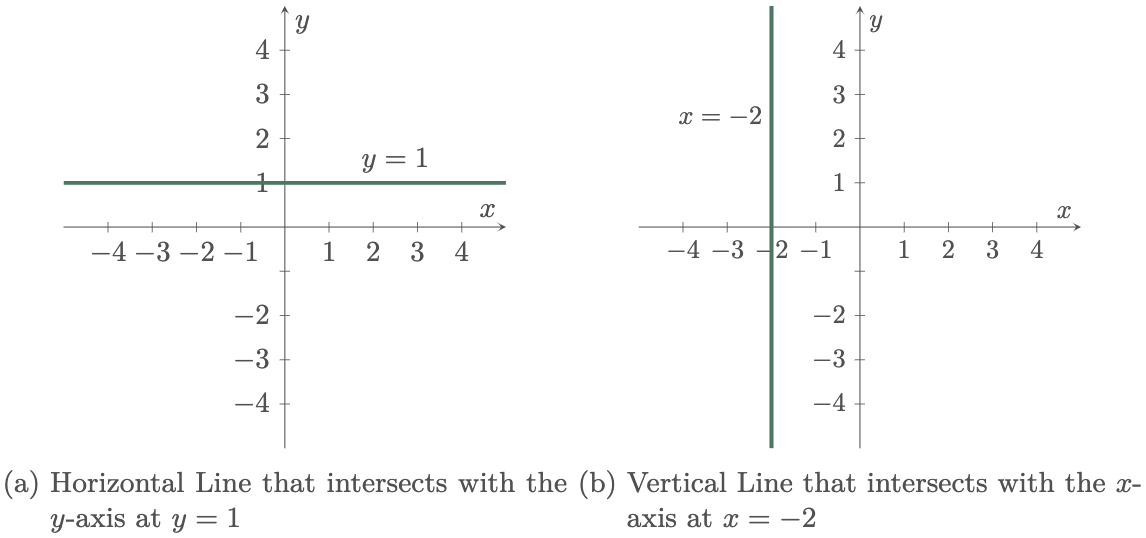
Figure 1: Horizontal and vertical lines

Figure 2: Axes of the Cartesian Plane expressed as an equation
For example, if we are to graph the area bounded by the curve $y=\frac{x^2}{5}+1$, the $x$-axis, $x = 1$, and $x = 4$ we can easily draw all the boundary lines and distinguish where the area is.
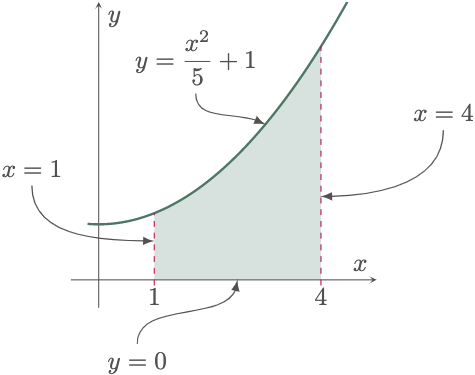
It is also a good practice to take note of the position of the boundaries with respect to another, since its orientation is crucial in using the formulas that we will introduce in the next section. Let us identify the position of each boundary in the previous example given.
- top: $y=\frac{x^2}{5}+1$
- bottom: $y=0$ ($x$-axis)
- left: $x=1$
- right: $x=4$