General Equation of a Plane Area
In solving for the area, there are two methods that can be taken into consideration. We can use a horizontal strip or a vertical strip, either of these will yield the same result. However, there are some problems that are preferably solved using one method than the other since it is much simpler. In order for us to determine what method to use, we fist need to learn the formulas of each method and how it is used.
Considering a Vertical Strip
In using the vertical strip to solve for the area, consider $\fref{1}$. The rectangular element of the vertical strip has a width of $dx$ and has a length of $y$. The lower and upper limits of the area are the left and right boundaries, respectively.
Moreover, the length of the strip $y$ is equal to the difference of the upper and lower boundaries $y=y_2-y_1$, this is oftentimes neglected in some references. However, it is a necessary detail in order to fully define the area. Also, in order for us not be confused when dealing with more than one curve, which we will tackle in the succeeding lessons. Mathematically, we can denote the formula as,
$$\begin{align} A = \int_{x_1}^{x_2} y\,dx \label{eq:area of integration using vertical strip} \end{align}$$
\[\begin{align*} \text{Where:}\quad y &= y_2-y_1 & \\ y_1 &= \text{equation of lower curve (bottom boundary)} \\ y_2 &= \text{equation of upper curve (top boundary)} \\ x_1 &= \text{lower limit (left boundary)} \\ x_2 &= \text{upper limit (right boundary)} \end{align*}\]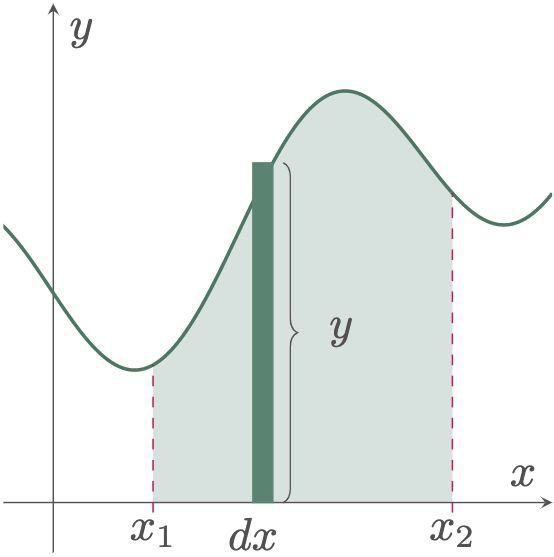
Figure 1: Area under a curve using a vertical strip
Considering a Horizontal Strip
The steps in solving the area using the horizontal strip are not that different from using the vertical strip. The significant difference between the two methods is the orientation of its boundaries. In using the horizontal strip in integrating for the area, the limits are the bottom and top boundaries, while the integrand is the difference between the right and left boundaries, $x=x_2-x_1$. Mathematically, the formula is expressed as,
$$\begin{align} A = \int_{y_1}^{y_2} x\,dy \label{eq:area of integration using horizontal strip} \end{align}$$
\[\begin{align*} \text{Where:}\quad x &= x_2-x_1 & \\ x_1 &= \text{equation of left curve (left boundary)} \\ x_2 &= \text{equation of right curve (right boundary)} \\ y_1 &= \text{lower limit (bottom boundary)} \\ y_2 &= \text{upper limit (top boundary)} \end{align*}\]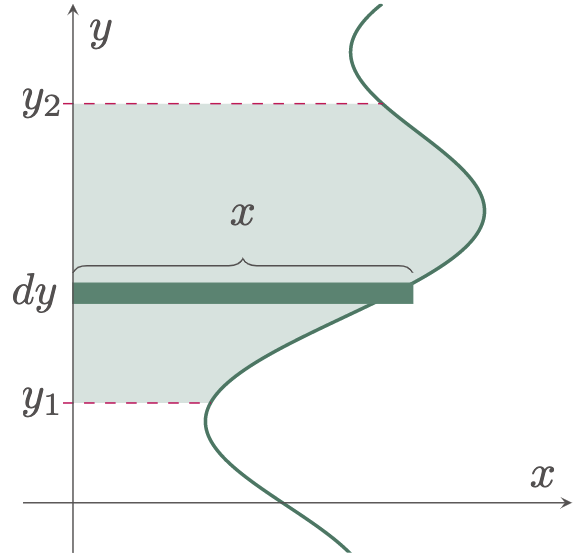
Figure 2: Area under a curve using a horizontal strip
To fully understand how to use these equations and how each can be more beneficial to use than the other. Let us have some examples.
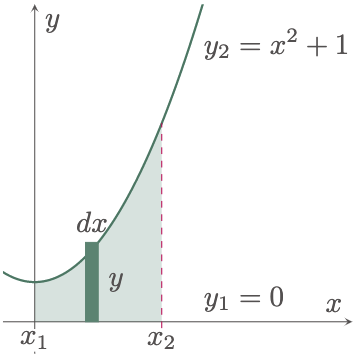
$\example{1}$ Compute the area bounded by the curve $y=x^2+1$, the $x$-axis, $x=0$, and $x=2$.
$\solution$
In solving for the area, the first step that we need to undergo everytime is to graph the boundaries. With this, we can visualize the graph and identify the position of each boundary with respect to each other.
$\typB{Considering a Vertical Strip,}$
$\example{2}$ Solve for the area bounded by the curve $y=x^2-4$ and the $x$-axis.
$\solution$
$\typB{Considering a Vertical Strip,}$
In this example, the left and right boundaries are defined by a point of intersection of the curve and the $x$-axis. Moreover, the curve is located below the $x$-axis. The steps in solving this type of problem are similar to the previous example, just that we will give a greater emphasis on the top and bottom boundaries, since in this case, the upper boundary is now the $x$-axis.
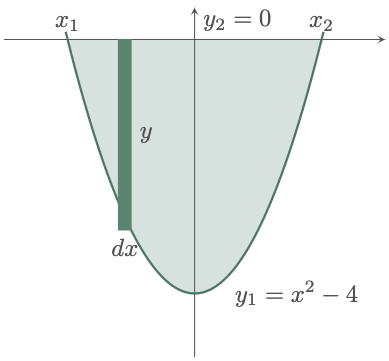
Before we can use the equation of the area, we still need to solve for the limits, which in this case are the points of intersection between the curve and the $x$-axis. To do that, we can first equate the two equations of the intersecting curves,
\[\begin{align*} y_1 &= y_2 \\ x^2-4 &= 0 \\ (x+2)(x-2) &= 0 \\ x+2 = 0 \qquad&;\qquad x-2 = 0 \end{align*}\]Solving for $x$ gives us,
\[\begin{align*} x_1 = -2 \qquad&;\qquad x_2 = 2 \end{align*}\]With all the parameters ready for substitution, we can now use $\eref{eq:area of integration using vertical strip}$,
\[\begin{align*} A &= \int_{x_1}^{x^2} y\,dx \\ &= \int_{x_1}^{x^2} \brk{y_2-y_1}\,dx \\ &= \int_{-2}^{2} \brk{0-(x^2-4)}\,dx \\ &= \int_{-2}^{2} \brk{-x^2+4}\,dx \\ &= \brk{-\frac{x^3}{3}+4x}_{-2}^2 \\ &= \brk{-\frac{2^3}{3}+4(2)} - \brk{-\frac{(-2)^3}{3}+4(-2)} \\ &= \brk{-\frac83+8}-\brk{\frac83-8} \\ &= \frac{32}{3}\un{units^2} \tagans \end{align*}\]$\typB{Considering a Horizontal Strip,}$
Using the horizontal strip, we cannot directly input the given parameters to the equation since the area’s left and right boundaries are of the same curve; doing so will lead to misdefined boundaries. However, a workaround in this situation is to first consider half of the area and double the result after since the area is symmetrical about the $y$-axis, which creates a mirror image of the other half.
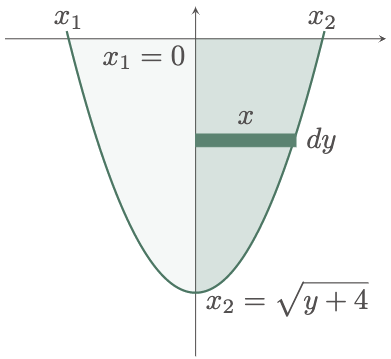
Before we can use the formula, we must first find the limits of the area. In this case, the top boundary is defined by $x$-axis or $y=0$, and the bottom boundary is a point of intersection between the curve and the $y$-axis. To solve for the point, we can equate the equations of the intersecting curves just as we did in the previous example,
\[\begin{align*} x_2 &= x_1 \\ \sqrt{y+4} &= 0 \\ y+4 &= 0 \\ y &= -4 \end{align*}\]Hence, the lower and upper limits are $y_1=-4$ and $y_2=0$, respectively.
\[\begin{align*} A_{\text{half}} &= \frac{A}{2} = \int_{y_1}^{y_2} x\,dy \\ A &= 2\int_{y_1}^{y_2} x\,dy \\ &= 2\int_{y_1}^{y_2} \brk{x_2-x_1}\,dy \\ &= 2\int_{-4}^{0} \brk{\sqrt{y+4}-0}\,dy \\ &= 2\brk{\frac23(y+4)^{3/2}}_{-4}^{0} \\ &= 2\brk{\brk{\frac23(0+4)^{3/2}} - \brk{\frac23\cancel{(-4+4)}^{3/2}}} \\ &= 2\cdot\frac{16}{3} \\ &= \frac{32}{3}\un{units^2} \tagans \end{align*}\]$\example{3}$ Find the area of the region bounded by the function $x=y^2-2y-3$ and the axes at the second quadrant.
$\solution$
Graphing the bounded area gives us,
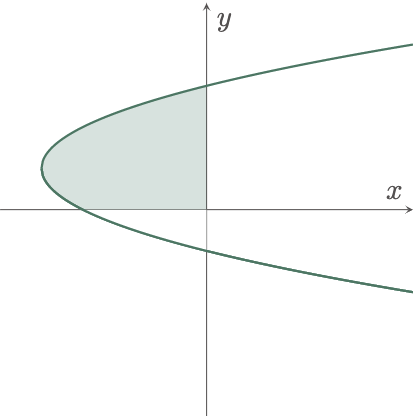
By inspection, we can see that using a horizontal strip is easier to solve the problem. Thus,
$\typB{Considering a Horizontal Strip,}$
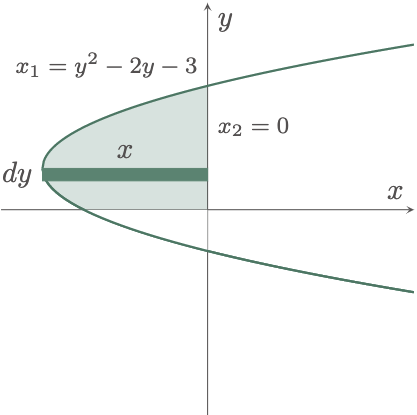
The lower limit of the area in considering a horizontal strip is the $x$-axis or $y=0$, and the upper limit is the intersection of the the curve and the $y$-axis. Hence, equating the curves gives us,
\[\begin{align*} x_1 &= x_2 \\ y^2-2y-3 &= 0 \\ \end{align*}\]To solve for $y$, we can use the method of “Completing the Square’’
\[\begin{align*} (y^2-2y {\tcA{+1}})-3 \tcA{-1} &= 0 \qquad\qquad \tcA{y^2-2y+1=(y-1)^2} \\ (y-1)^2-4 &= 0 \\ (y-1)^2 &= 4 \\ y &= \pm\sqrt{4}+1 \end{align*}\]Breaking down the two possible result of the sqare root gives us,
\[\begin{align*} y = -\sqrt{4}+1 \qquad&;\qquad y = +\sqrt{4}+1 \\ y = -2+1 \qquad&;\qquad y = 2+1 \\ y = -1 \qquad&;\qquad y = 3 \end{align*}\]Since the curves intersect at two points, it is expected that we will have two results. However, in our case we only need one, specifically the $y=3$. Hence, the lower and upper limits are $y_1=0$ and $y_2=3$, respectively.
\[\begin{align*} A &= \int_{y_1}^{y^2} x\,dy \\ &= \int_{y_1}^{y^2} [x_2-x_1]\,dy \\ &= \int_{0}^{3} \brk{0-(y^2-2y-3)}\,dy \\ &= \brk{-\frac{y^3}{3}+\frac{2y^2}{2}+3y}_0^3 \\ &= \brk{-\frac{3^3}{3}+\frac{2(3)^2}{2}+3(3)} - \cancel{\brk{-\frac{(0)^3}{3}+\frac{2(0)^2}{2}+3(0)}} \\ &= 9\un{units^2} \tagans \end{align*}\]$\example{4}$ Find the area of the region bounded by the function $x^2-6x+8$, the $x$-axis, and the vertical lines $x=0$ and $x=5$.
$\solution$
Graphing the bounded area gives us,
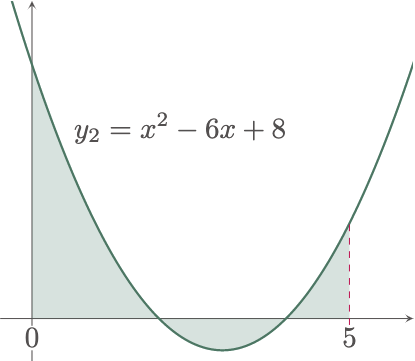
The area is divided into three parts, each having different boundaries. In this case, we must treat each sub-area differently, ultimately summing up the values to determine the whole area. By inspection, we can also see that using a vertical stip is easier to solve the problem.
First, we need to pinpoint the intersection points between the curve and the $x$-axis since it serves as the new limits for the sub-areas.
\[\begin{align*} y_2 &= y_1 \\ x^2-6x+8 &= 0 \\ \end{align*}\]By “Completing the Square’’,
\[\begin{align*} (x^2-6x {\tcA{+9}})+8 \tcA{-9} &= 0 \\ (x-3)^2-1 &= 0 \\ x &= \pm\sqrt{1}+3 \end{align*}\]Breaking down the two possible result of the sqare root gives us,
\[\begin{align*} x = -\sqrt{1}+3 \qquad&;\qquad x = +\sqrt{1}+3 \\ x = -1+3 \qquad&;\qquad x = 1+3 \\ x = 2 \qquad&;\qquad x = 4 \\ \end{align*}\]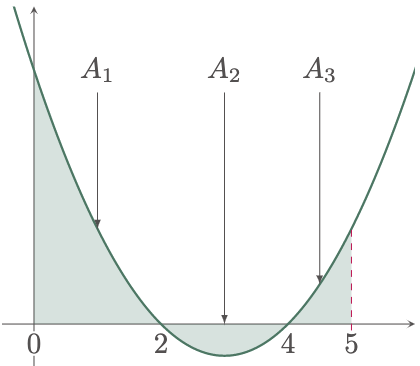
Hence,
\[\begin{align*} A &= A_1 + A_2 + A_3 \\ &= \int_0^2 \brk{y_2-y_1}\,dx + \int_2^4 \brk{y_1-y_2}\,dx + \int_4^5 \brk{y_2-y_1}\,dx \\ &= \int_0^2 \brk{(x^2-6x+8)-0}\,dx + \int_2^4 \brk{0-(x^2-6x+8)}\,dx \\ &\qquad + \int_4^5 \brk{(x^2-6x+8)-0}\,dx \\ &= \int_0^2 \brk{x^2-6x+8}\,dx + \int_2^4 \brk{-x^2+6x-8}\,dx + \int_4^5 \brk{x^2-6x+8}\,dx \\ &= \int_0^2 \brk{x^2-6x+8}\,dx - \int_2^4 \brk{x^2-6x+8}\,dx + \int_4^5 \brk{x^2-6x+8}\,dx \\ &= \brk{\frac{x^3}{3}-3x^2+8x}_0^2 - \brk{\frac{x^3}{3}-3x^2+8x}_2^4 + \brk{\frac{x^3}{3}-3x^2+8x}_4^5 \\ &= \brk{\br{\frac{2^3}{3}-3(2)^2+8(2)}-\br{\frac{0^3}{3}-3(0)^2+8(0)}} + \left[\br{\frac{4^3}{3}-3(4)^2+8(4)} \right. \\ &\qquad - \left.\br{\frac{(2)^3}{3}-3(2)^2+8(2)} \right] + \brk{\br{\frac{5^3}{3}-3(5)^2+8(5)} - \br{\frac{4^3}{3}-3(4)^2+8(4)}} \\ &= \brk{\frac{20}{3}-0} - \brk{\frac{16}{3}-\frac{20}{3}} + \brk{\frac{20}{3}-\frac{16}{3}} \\ &= \frac{20}{3} - \frac{16}{3} + \frac{20}{3} + \frac{20}{3} - \frac{16}{3} \\ &= \frac{28}{3}\un{sq.units} \tagans \end{align*}\]$\example{5}$ Compute the area at the first quadrant of the region bounded by the function $y=3\cos\frac12x$, $x=0$, and $y=0$.
$\solution$
$\typB{Considering a Vertical Strip,}$
Graphing the bounded area gives us,
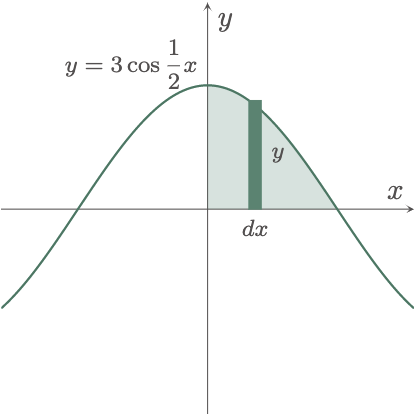
The lower limit of the area is the $y$-axis or $x=0$. However, we still need to solve for the upper limit, which is the $x$-coordinate of the point of intersection of the curve and the $x$-axis. Hence, equating the equations of the two curves,
\[\begin{align*} 3\cos\frac12x &= 0 \\ \cos\frac12x &= 0 \\ \frac12x &= \cos^{-1}(0) \\ \frac12x &= \frac{\pi}{2} \\ x &= \pi \end{align*}\]Hence,
\[\begin{align*} A &= \int_{x_1}^{x_2} \brk{y_2-y_1}\,dx \\ &= \int_0^\pi \brk{3\cos\frac12x - 0}\,dx \\ &= \brk{6\sin\frac12x}_0^{\pi} \\ &= \brk{6\sin\frac\pi2} - \brk{6\sin\frac02} \\ &= 6-0 \\ &= 6\un{sq.units} \tagans \end{align*}\]
