To describe the location of a point on a plane, two independent measurements are required. This idea forms the basis of the Cartesian plane. A Cartesian plane is made up of two number lines that are perpendicular to each other. The horizontal number line is called the $x$-axis, and the vertical number line is called the $y$-axis. Any point on the plane can be described using an ordered pair of numbers $(x, y)$. The first number, represented by the variable $x$, is called the $x$-coordinate or the abscissa, while the second number, represented by the variable $y$, is called the $y$-coordinate or the ordinate. The point where the two axes intersect is called the origin, whose coordinates are $(0, 0)$.
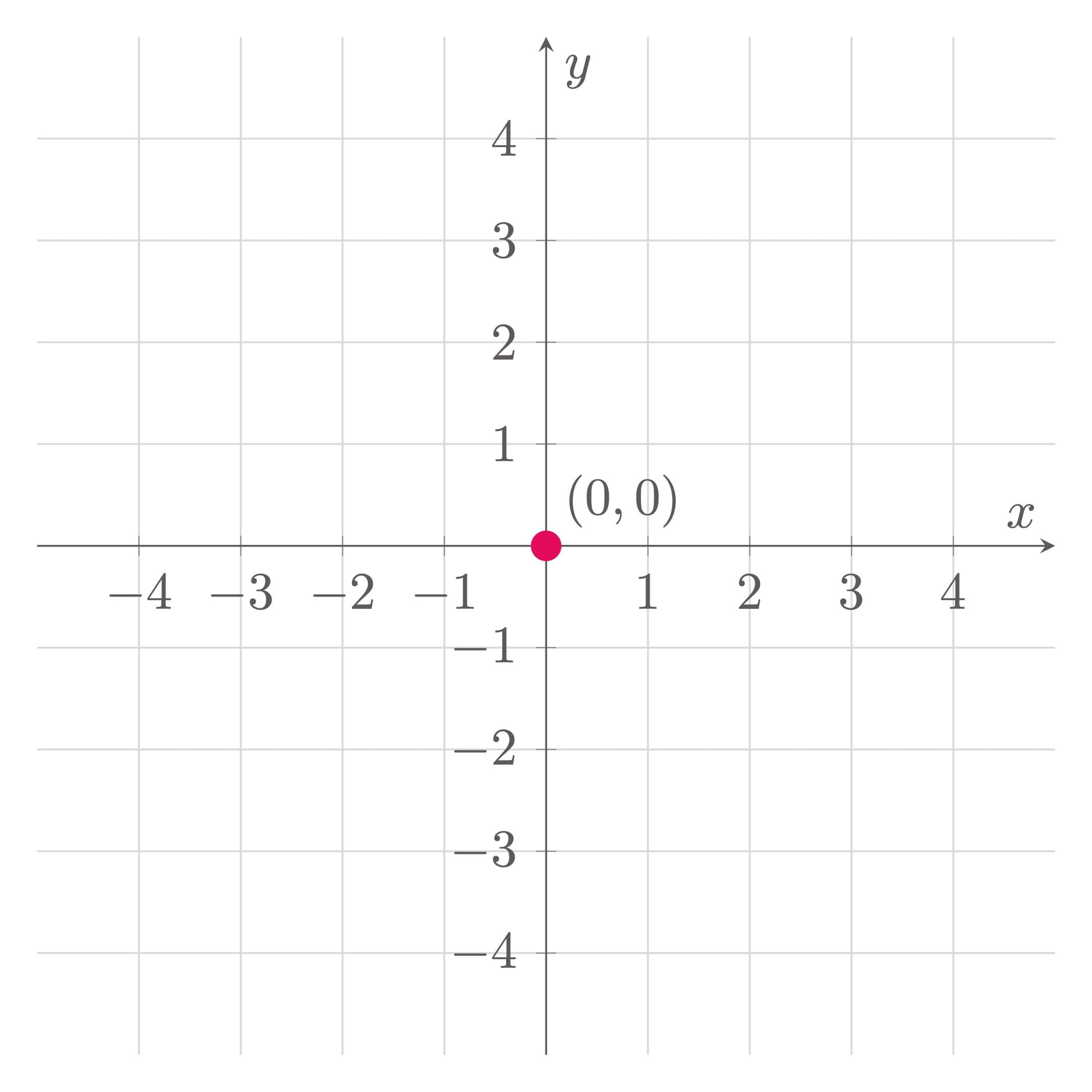
Figure 1: The Cartesian plane and the origin
A point in a Cartesian plane is measured relative to the origin. The $x$-coordinate defines the horizontal distance of the point from the origin. If the point is positioned on the right side relative to the origin, its value is positive, and if it is positioned on the left side, its value is negative. The $y$-coordinate defines the vertical position of the point from the origin. It is positive when the point is located above the origin, and negative when it is located below it, as illustrated in Figure 2.
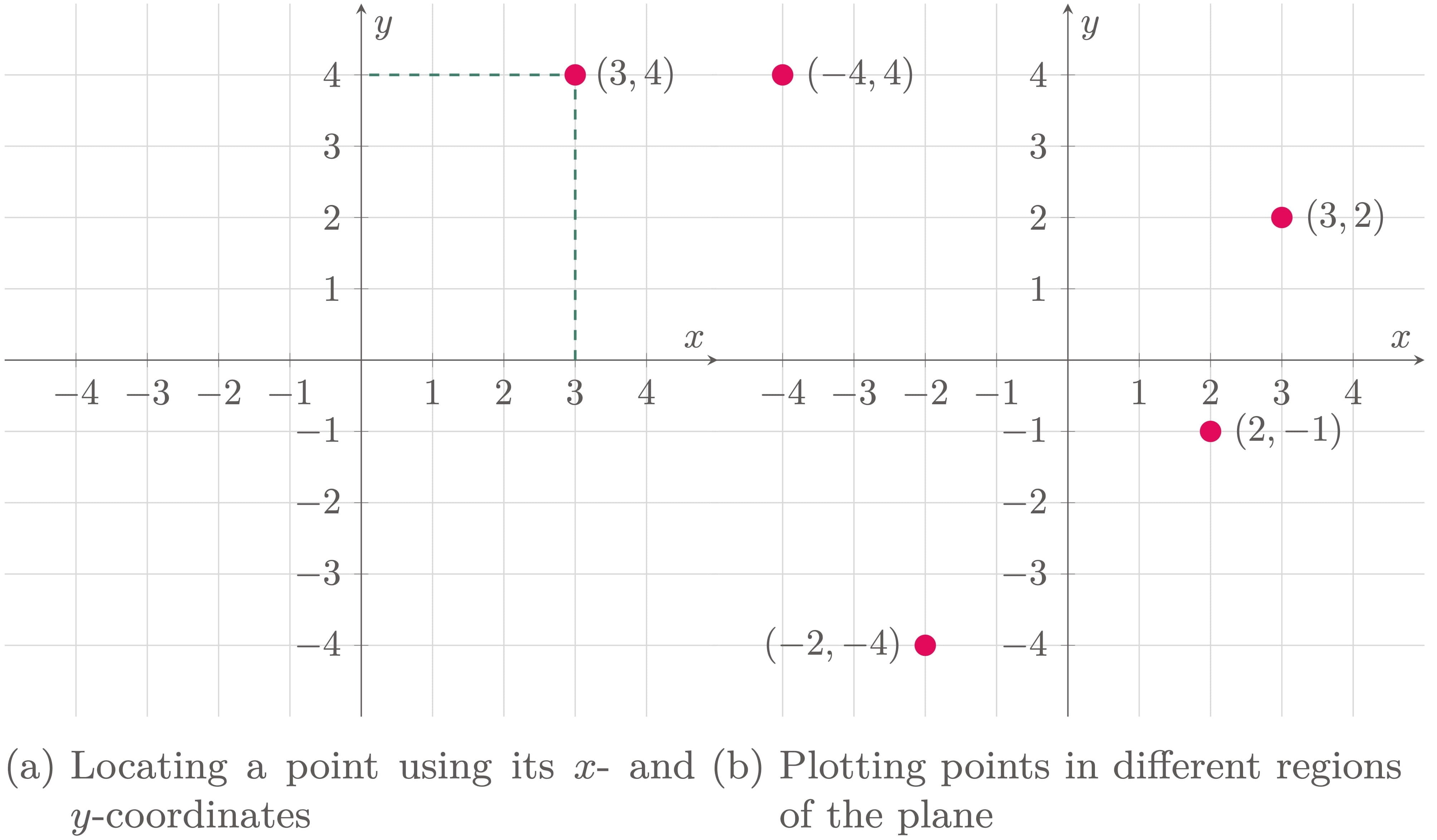
Figure 2: Representing ordered pairs on the Cartesian plane
The Cartesian plane is divided into four regions, which are called quadrants, and are denoted by the Roman numerals I, II, III, and IV. In the first quadrant, both the abscissa and the ordinate are positive. In the second quadrant, the abscissa is negative while the ordinate is positive. In the third quadrant, both the abscissa and the ordinate are negative. In the fourth quadrant, the abscissa is positive while the ordinate is negative (Figure 3).
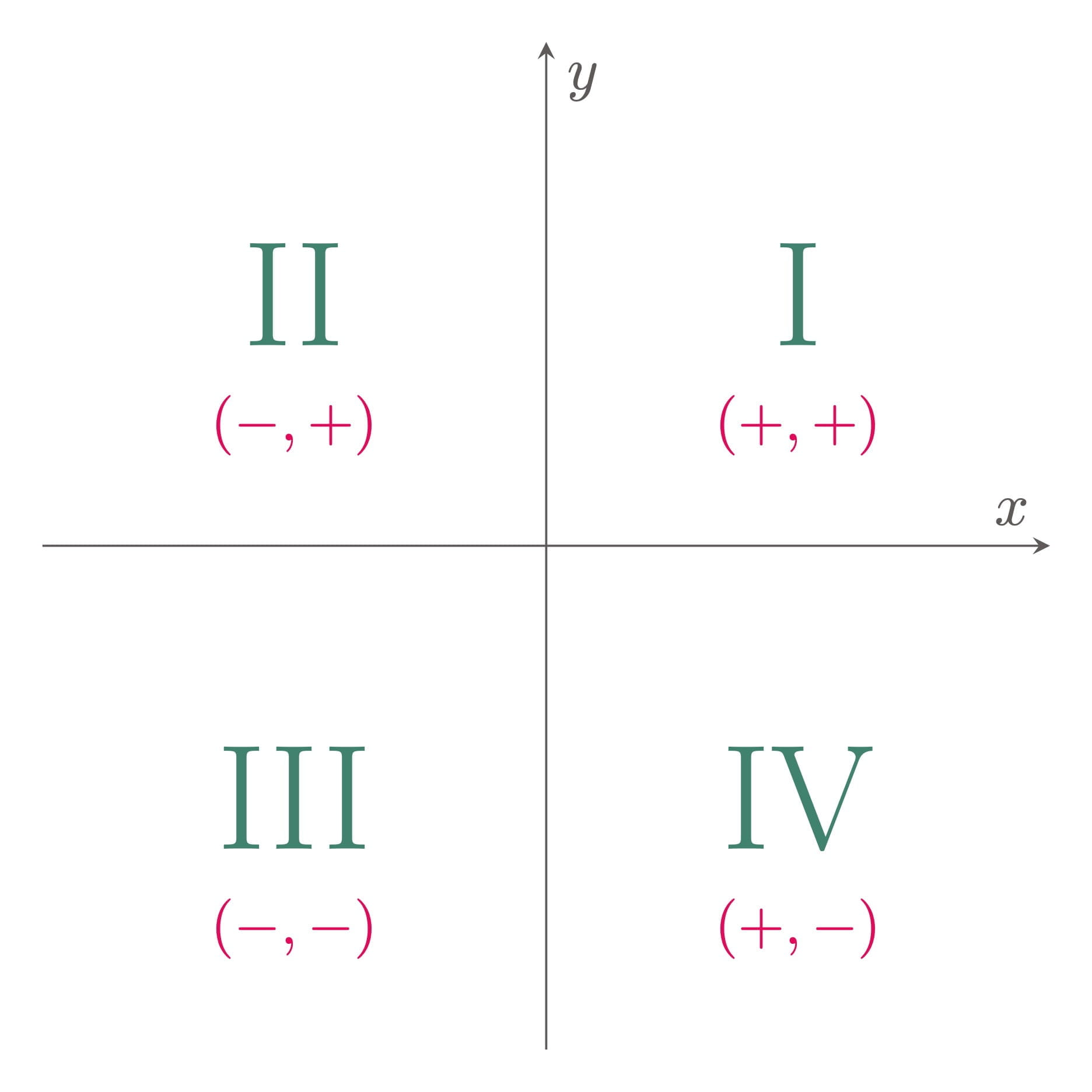
Figure 3: Quadrants and sign conventions
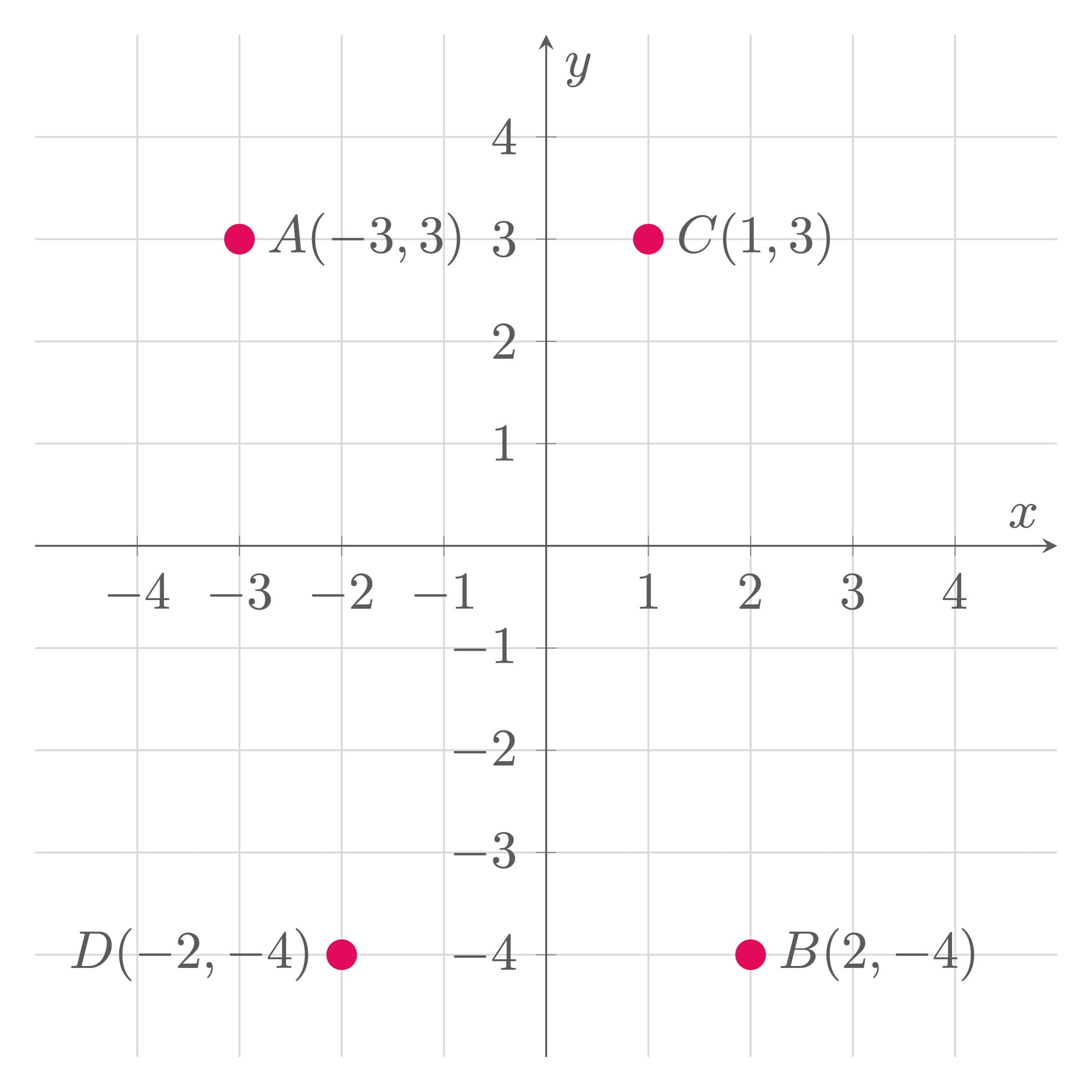
$\example{1}$ Plot the following points in a cartesian plane. $A(-3,3)$, $B(2,-4)$, $C(1,3)$, and $D(-2,-2)$
$\solution$
Locate the points on the cartesian plane,
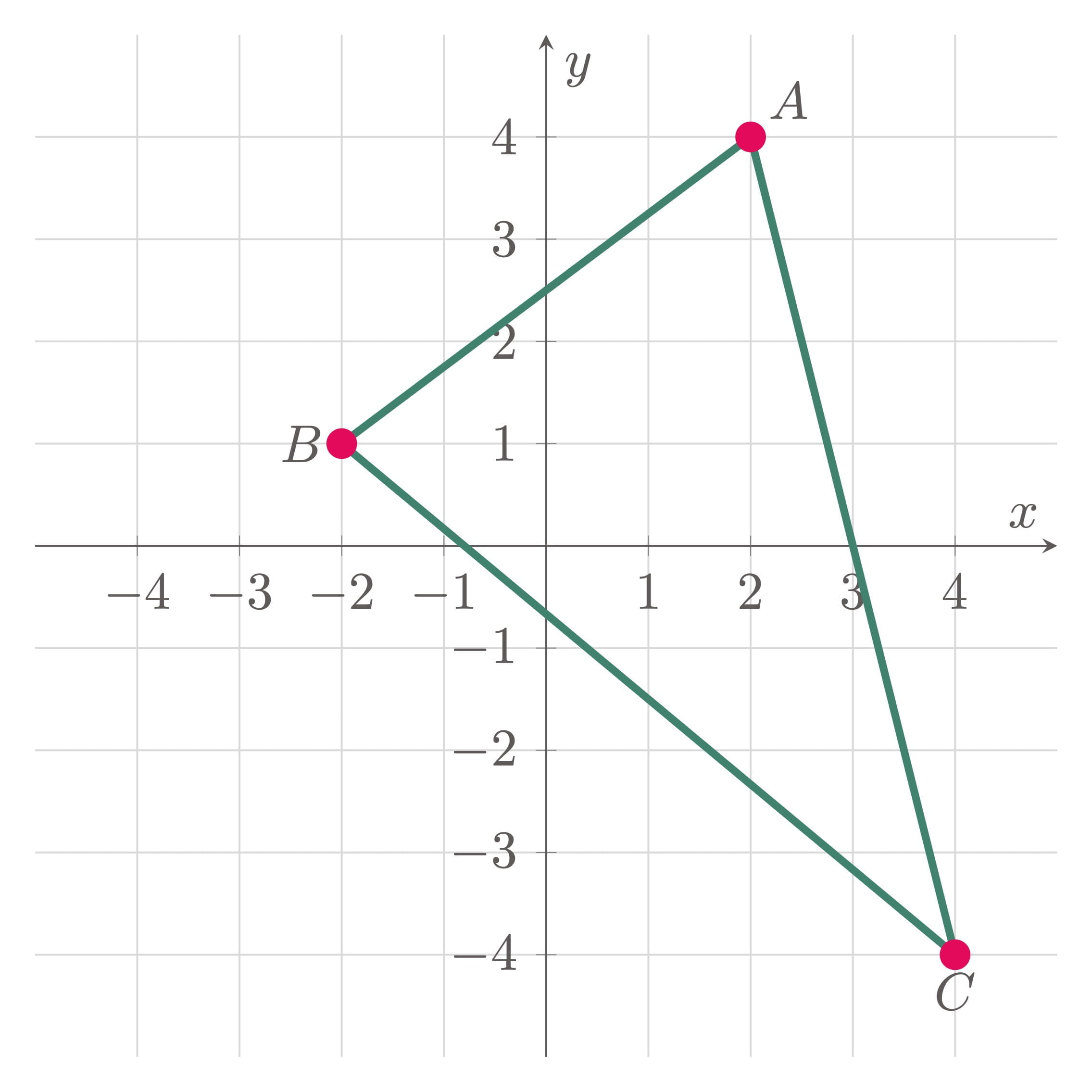
$\example{2}$ Plot the triangle that has vertices of $(2,4)$, $(-2,-1)$, and $(4,-4)$
$\solution$
To plot the triangle, first locate the points on the cartesian plane, then connect each points with line segments