The distance between two points that lie on the same plane can be represented by the length of the line segment connecting the points. This length corresponds to the shortest possible path between the two given points and can be derived using the Pythagorean theorem. Consider Figure 1.
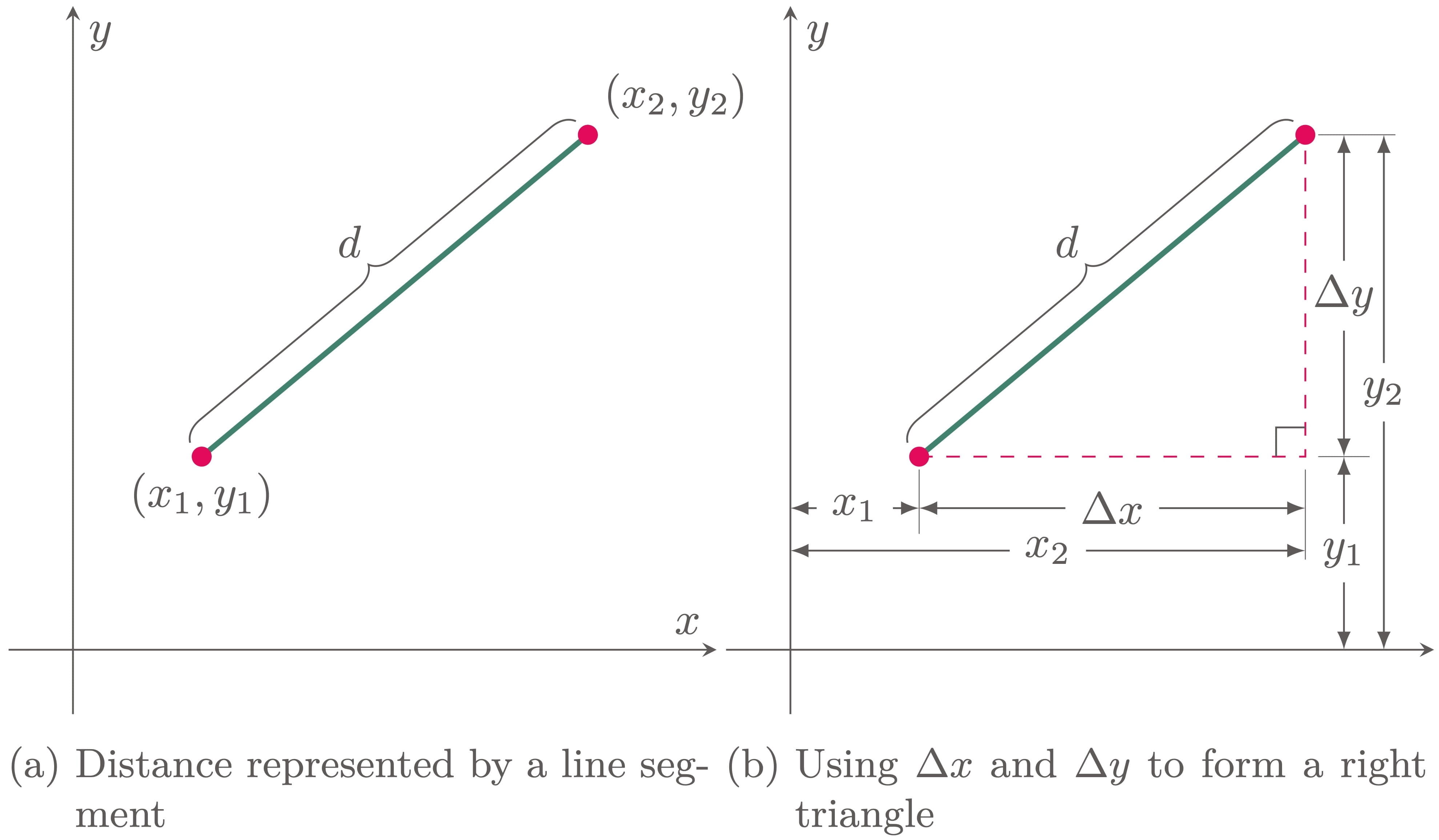
Figure 1: Deriving the distance formula using the Pythagorean theorem
Let $\Delta x$ and $\Delta y$ represent the lengths of the legs of the right triangle formed, and let $d$ represent the length of its hypotenuse. Applying the Pythagorean theorem gives
\[\begin{align*} d^2 &= \Delta x^2 + \Delta y^2 \\ d^2 &= (x_2-x_1)^2 + (y_2-y_1)^2 \\ \end{align*}\]Taking the square root of both sides yields
$$\begin{align} d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} \end{align}$$
Equation 1 is called the Distance Formula. This equation is useful in determining the shortest possible distance between any two points that lie on the same plane.
$\example{1}$ Find the distance between $A(4, -3)$ and $B(-2, 5)$.
$\solution$
To determine the distance between the given points, use Equation 1.
\[\begin{align*} d &= \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} \\ &= \sqrt{(-2-4)^2 + [5-(-3)]^2} \\ &= \sqrt{(-6)^2 + 8^2} \\ &= \sqrt{100} \\ &= 10 \tagans \end{align*}\]$\example{2}$ The point $(x, 1)$ is $2\sqrt{5}$ units from $(2, 3)$. Find $x$.
$\solution$
To solve for $x$, use Equation 1.
\[\begin{align*} d &= \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} \\ 2\sqrt{5} &= \sqrt{(2-x)^2 + (3-1)^2} \\ 2\sqrt{5} &= \sqrt{(4 - 4x + x^2) + 4} \end{align*}\]Square both sides.
\[\begin{align*} (2\sqrt{5})^2 &= \br{\sqrt{x^2 - 4x + 8}}^2 \\ 20 &= x^2 - 4x + 8 \\ x^2 - 4x - 12 &= 0 \end{align*}\]Factor the resulting quadratic equation.
\[\begin{align*} (x-6)(x+2) &= 0 \end{align*}\]Hence,
\[\begin{align*} (x-6) &= 0 & (x+2) &= 0 \\ x &= 6 & x &= -2 \tagans \end{align*}\]$\example{3}$ If the point $C(x,4)$ is equidistant from $A(5,-2)$ and $B(3,4)$, determine the value of $x$.
$\solution$
Since point $C$ is equidistant from points $A$ and $B$, the distances from $C$ to $A$ and from $C$ to $B$ are equal. Thus,
\[\begin{align*} d_{AC} &= d_{BC} \\ \sqrt{(x_C-x_A)^2 + (y_C-y_A)^2} &= \sqrt{(x_C-x_B)^2 + (y_C-y_B)^2} \\ \sqrt{(x-5)^2 + [4-(-2)]^2} &= \sqrt{(x-3)^2 + (4-4)^2} \\ \br{\sqrt{x^2 - 10x + 25 + 36}}^2 &= \br{\sqrt{x^2 - 6x + 9}}^2 \\ \cancel{x^2} - 10x + 61 &= \cancel{x^2} - 6x + 9 \\ 4x &= 52 \\ x &= 13 \tagans \end{align*}\]
