The point on a line that bisects a line segment is called the midpoint of a line. Consider Figure 1. The line segment $\overline{AB}$ has a midpoint at point $P$. The coordinates of the midpoint, denoted by $(x, y)$, can be determined by taking the average of the abscissas and the ordinates of the two endpoints.
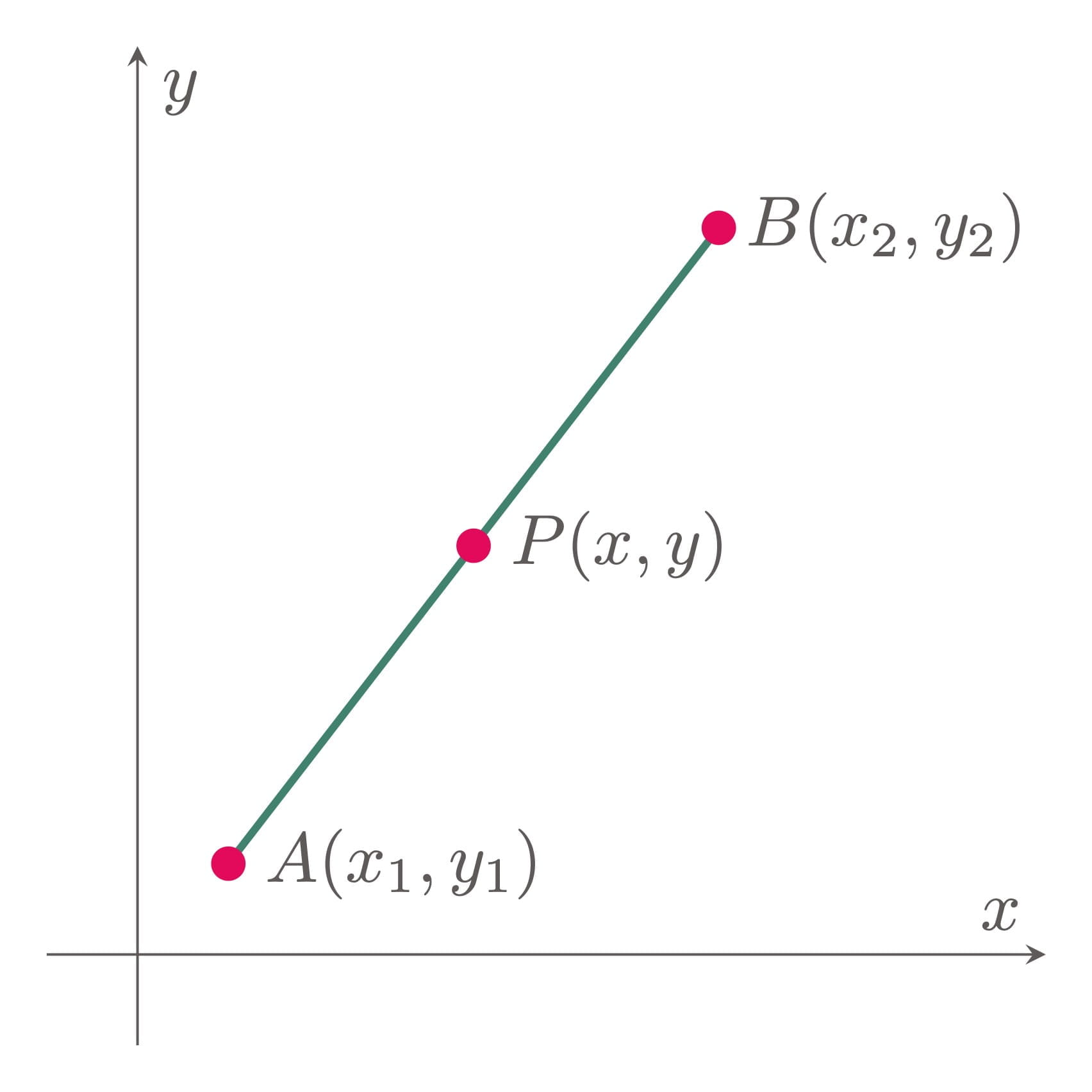
Figure 1: The midpoint $P(x,y)$ of the line segment $\overline{AB}$
Hence, if the line segment $\overline{AB}$ is bisected at point $P$, the coordinates of the midpoint are given by
$$\begin{align} P(x,y) = \br{ \frac{x_1+x_2}{2}, \frac{y_1+y_2}{2} } \label{eq:midpoint formula} \end{align}$$
$\example{1}$ Find the midpoint of the line segment connecting $(-5,-2)$ and $(3,4)$.
$\solution$
To determine the coordinates of the midpoint of the line segment, use Equation \ref{eq:midpoint formula}. \(\begin{align*} P(x,y) &= \br{ \frac{x_1+x_2}{2}, \frac{y_1+y_2}{2} } \\ &= \br{ \frac{-5+3}{2}, \frac{-2+4}{2} } \\ &= \br{ \frac{-2}{2}, \frac{2}{2} } \\ &= (-1,1) \tagans \end{align*}\)
$\example{2}$ The line segment connecting $(x, 6)$ and $(9, y)$ is bisected by the point $(7, 3)$. Find the values of $x$ and $y$.
$\solution$
Consider the $x$-coordinate of the midpoint.
\[\begin{align*} x &= \frac{x_1+x_2}{2} \\ 7 &= \frac{x+9}{2} \\ 14 &= x+9 \\ x &= 5 \tagans \end{align*}\]Similarly, solve for the $y$-coordinate.
\[\begin{align*} y &= \frac{y_1+y_2}{2} \\ 3 &= \frac{6+y}{2} \\ 6 &= 6+y \\ y &= 0 \tagans \end{align*}\]
