A line segment can also be divided into any desired ratio. In Figure 1a, point $P$ divides the line segment $\overline{AB}$ in the ratio $m:n$. The coordinates of point $P$ can be derived by constructing two similar triangles that also have a ratio of $m:n$, as shown in Figure 1b.
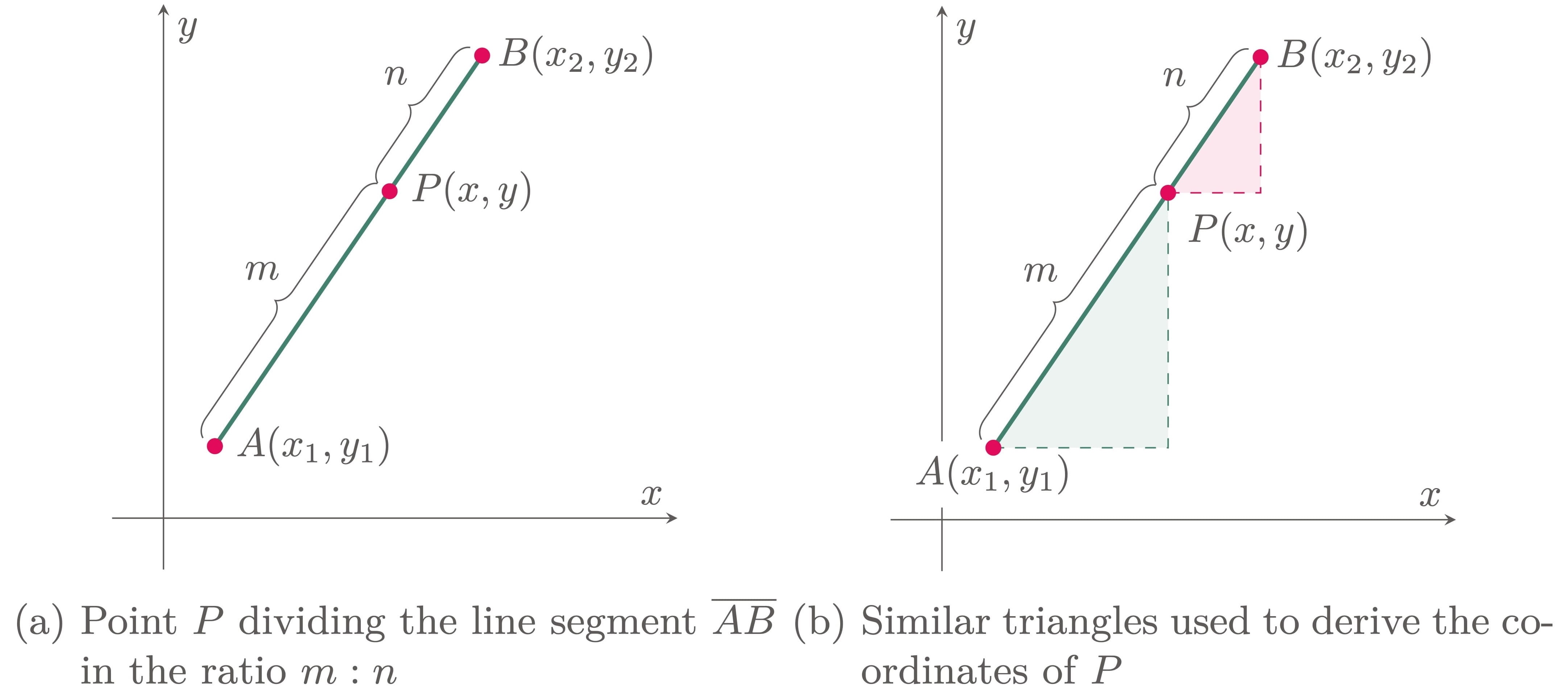
Figure 1: Finding the coordinates of a point that divides a line segment in a given ratio
Since the corresponding sides of similar triangles are proportional, the line segments $\overline{AP}$ and $\overline{AB}$ have a ratio of
\[\begin{align*} \frac{AP}{AB} &= \frac{m}{m+n} \end{align*}\]To determine the coordinates of point $P$, consider first the $x$-coordinate.
\[\begin{align*} \frac{x-x_1}{x_2-x_1} &= \frac{m}{m+n} \\ x-x_1 &= (x_2-x_1)\frac{m}{m+n} \\ x &= \frac{mx_2 - mx_1}{m+n}+x_1\\ &= \frac{mx_2 - mx_1 + x_1(m+n)}{m+n}\\ &= \frac{mx_2 + nx_1}{m+n} \end{align*}\]The $y$-coordinate can be obtained in a similar manner,
\[\begin{align*} y &= \frac{my_2 + ny_1}{m+n}\\ \end{align*}\]Hence, when the line segment $\overline{AB}$ is divided in the ratio $m:n$, the coordinates of point $P$ are given by
$$\begin{align} P(x,y) = \br{ \frac{mx_2 + nx_1}{m+n}, \frac{my_2 + ny_1}{m+n} } \label{eq:div of line} \end{align}$$
$\example{1}$ Determine the coordinates of the point that is three-fifths of the way from the point $(2, -5)$ to the point $(-3, 5)$.
$\solution$
To determine the coordinates of the point located three-fifths of the way from $(2, -5)$ to $(-3, 5)$, use Equation \ref{eq:div of line}, where $m = 3$ and $n = 2$.