Lines in a plane can be described not only by their position but also by their direction and steepness. These characteristics can be expressed geometrically using angles and numerically using ratios. In this section, the concepts of inclination and slope are introduced to describe the orientation of a line in the Cartesian plane.
Inclination, $\theta$
The inclination of a line is the angle formed by the line with the $x$-axis, where the angle is measured from the positive $x$-axis in a counter-clockwise direction. It is usually denoted by the Greek symbol theta, $\theta$.
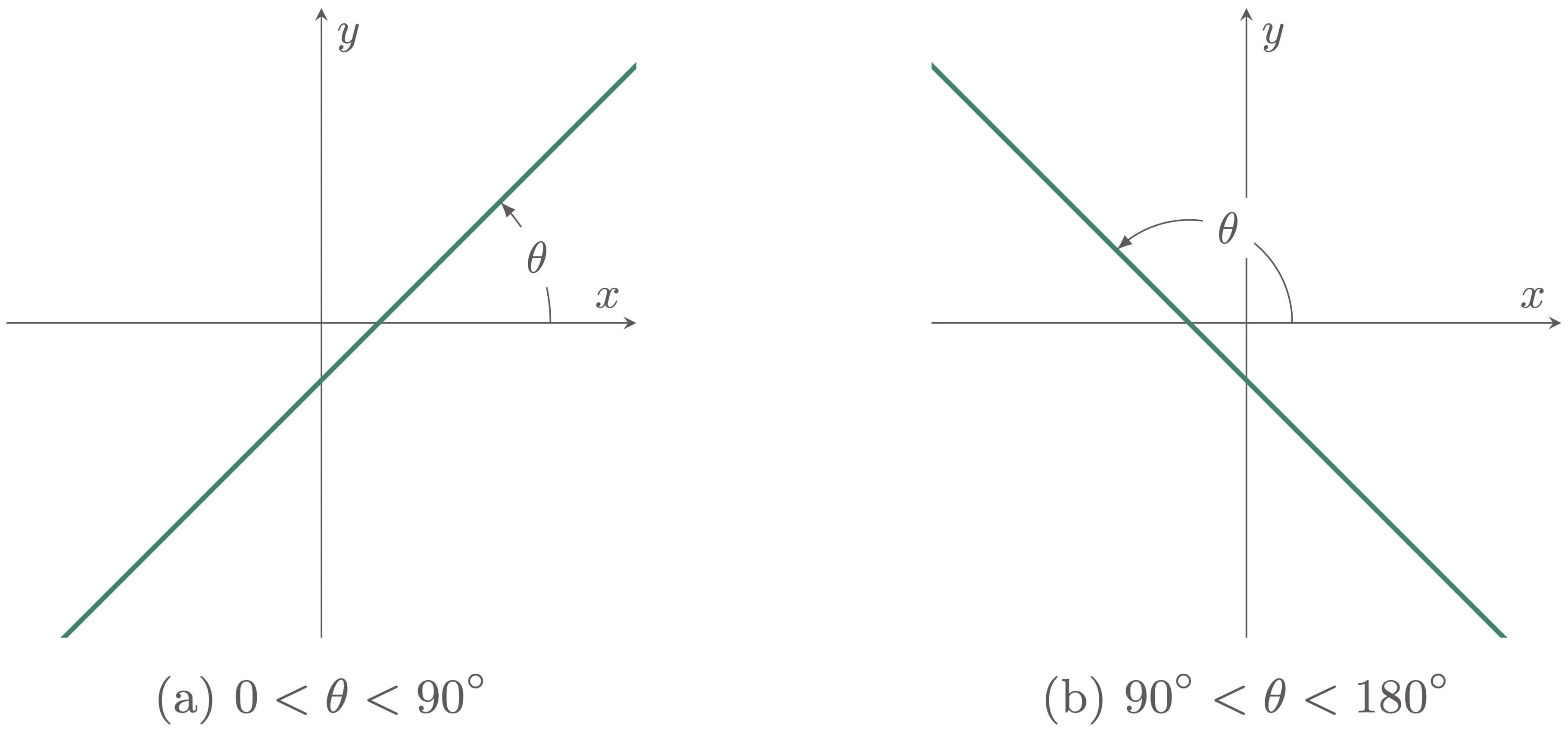
Figure 1: Angles of inclination measured from the positive $x$-axis
Slope, $m$
The slope of a line measures its steepness and direction. It is defined as the ratio of the change in the $y$-coordinates to the change in the $x$-coordinates between two points on the line, which is usually referred to as the ``rise over run.’’ Consider Figure 2.
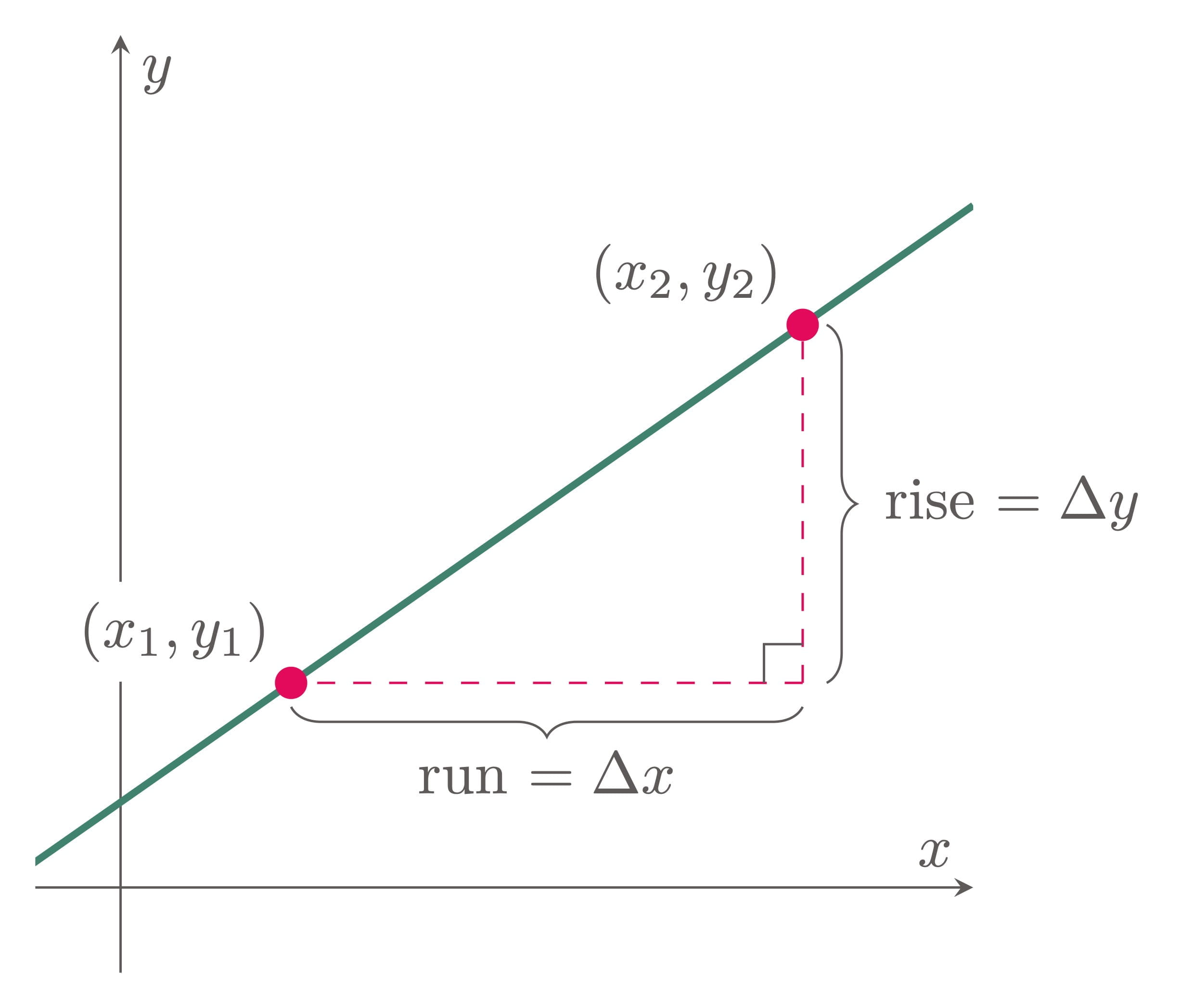
Figure 2: Slope as rise over run
$$\begin{align} m = \frac{\text{rise}}{\text{run}} = \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1} \label{eq:slope formula} \end{align}$$
The larger the numerical value of the slope, the steeper the line becomes. The sign of the slope indicates its direction. A positive slope $(+)$ means that the line rises to the right, while a negative slope $(-)$ means that the line falls to the right (Figure 3).
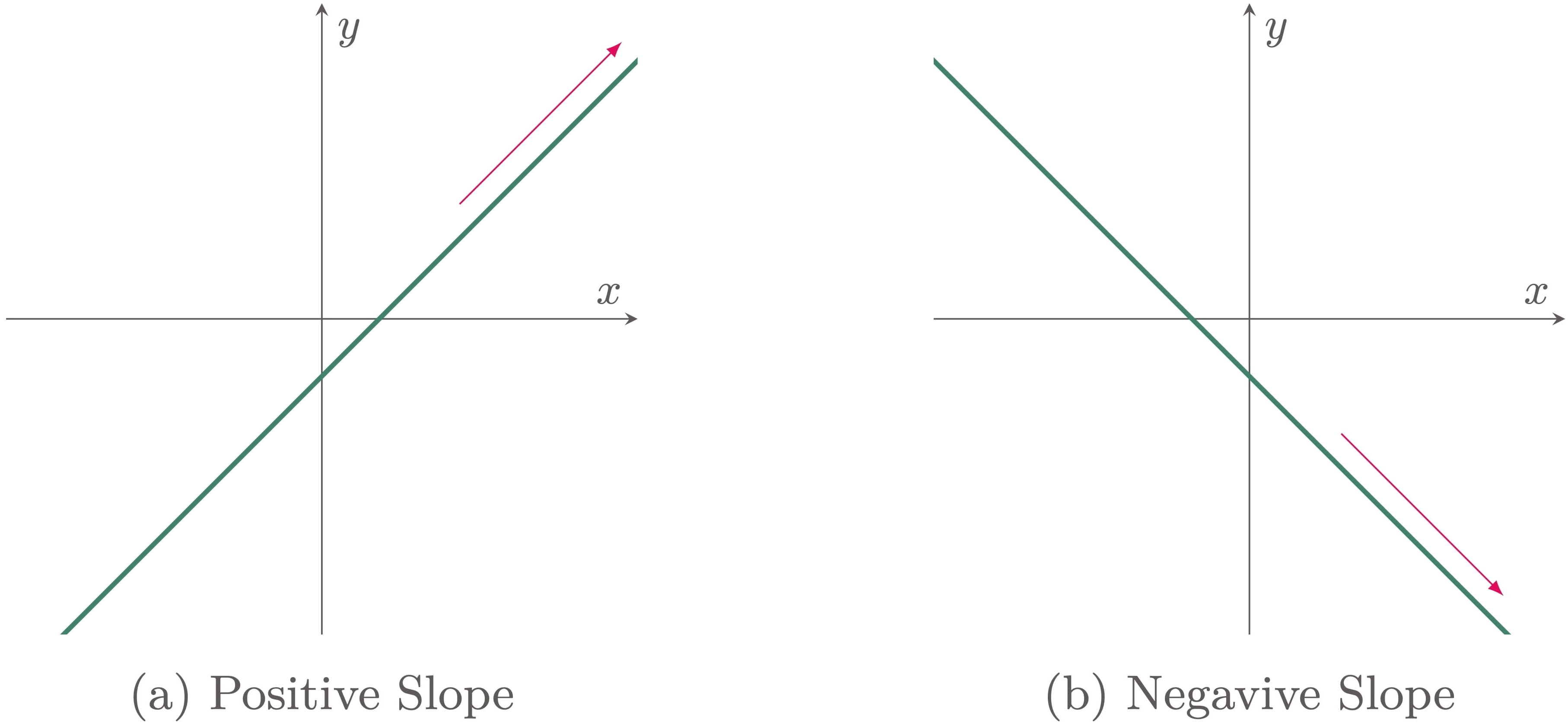
Figure 3: Direction of a line based on the sign of its slope
The relationship between the inclination and the slope of the same line can be established using trigonometric ideas. In particular, when a line forms a right triangle with the coordinate axes, the tangent of its angle of inclination relates the vertical change to the horizontal change (Figure 4).
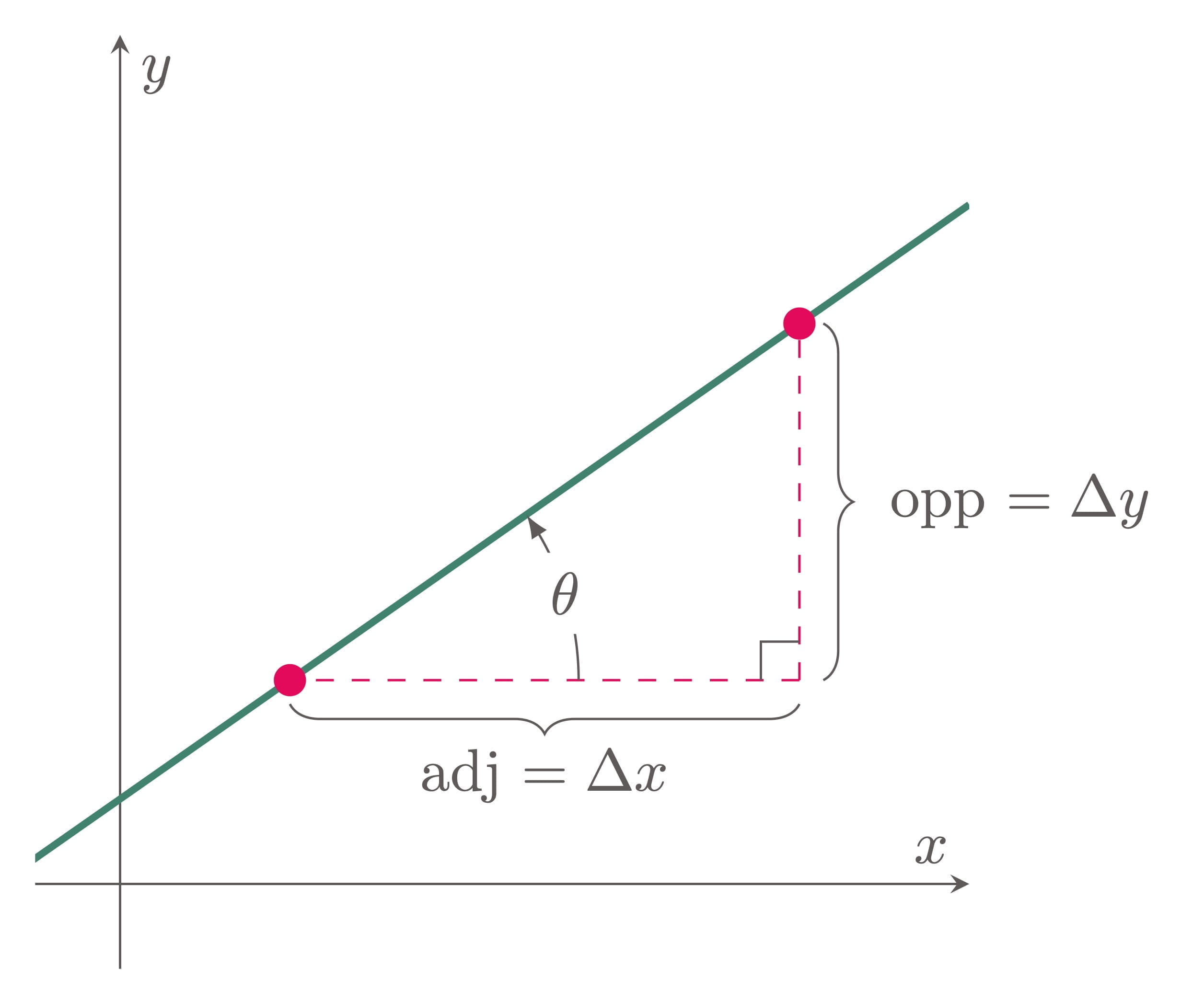
Figure 4: Relationship between slope and inclination
Thus, the slope of a line is equal to the tangent of its angle of inclination. This relationship allows the inclination of a line to be determined from its slope, and vice versa, and will be revisited in greater detail when we reach trigonometry.
$$\begin{align} \tan\theta = m \label{eq:tan m} \end{align}$$
$\example{1}$ Determine the slope of the line that passes through the points $(-4,-2)$ and $(6,4)$.
$\solution$
To solve for the slope from two given points, use Equation \ref{eq:slope formula}
\[\begin{align*} m &= \frac{y_2-y_1}{x_2-x_1} \\ &= \frac{4-(-2)}{6-(-4)} \\ &= \frac{6}{10} \\ &= \frac{3}{5} \tagans \end{align*}\]$\example{2}$ Determine the inclination of the line that has a slope of $2/5$.
$\solution$
To solve for the inclination, use the relationship between the inclination and the slope (Equation \ref{eq:tan m})
\[\begin{align*} \tan\theta &= m \\ \theta &= \tan^{-1}\br{ \frac{2}{5} } \\ &= 21.80^{\circ} \tagans \end{align*}\]$\example{3}$ Determine the inclination of the line that passes through the points $(-3,8)$ and $(2,-5)$.
$\solution$
To solve for the inclination, use Equation \ref{eq:tan m},
\[\begin{align*} \tan\theta &= m \\ \theta &= \tan^{-1}m \\ &= \tan^{-1}\br{ \frac{y_2-y_1}{x_2-x_1} } \\ &= \tan^{-1}\brk{ \frac{(-5)-8}{2-(-3)} } \\ &= \tan^{-1}\brk{ \frac{-13}{5} } \\ &= -68.96^{\circ} \end{align*}\]The angle obtained is a negative value, which represents the principal angle measured clockwise from the positive $x$-axis. However, the inclination of a line is defined as the angle measured counterclockwise from the positive $x$-axis. Therefore, the inclination is obtained by adding $180^{\circ}$:
\[\begin{align*} \theta &= - 68.96^{\circ} + 180^{\circ} \\ &= 111.04^{\circ} \tagans \end{align*}\]Horizontal and Vertical Lines
Slopes can also be zero or undefined. A zero slope occurs when the numerator of the slope formula is zero, indicating that there is no change in the $y$-coordinates between any two points on the line. As a result, the line is horizontal.
An undefined slope occurs when the denominator of the slope formula is zero, since division by zero is undefined. This situation indicates that there is no change in the $x$-coordinates between any two points on the line, resulting in a vertical line. Figure 5 illustrates horizontal and vertical lines along with their respective slopes.

Figure 5: Horizontal and Vertical Lines
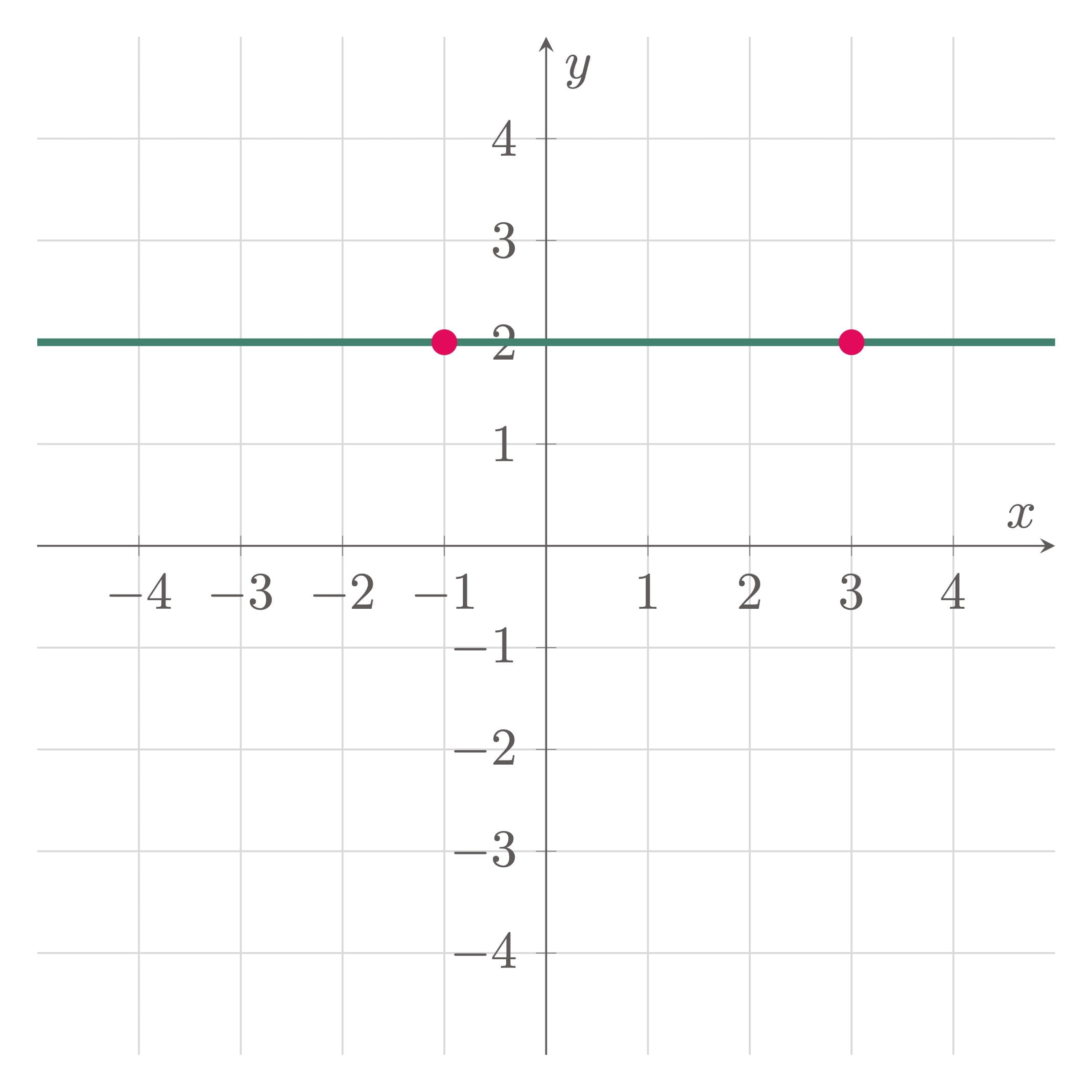
$\example{4}$ Determine the slope of the line that passes through the points $(3,2)$ and $(-1,2)$. Graph the line.
$\solution$
To solve for the slope use Equation \ref{eq:slope formula}
\[\begin{align*} m &= \frac{y_2-y_1}{x_2-x_1} \\ &= \frac{2-2}{-1-3} \\ &= \frac{0}{-4} \\ &= 0 \tagans \end{align*}\]Hence, the line is horizontal.
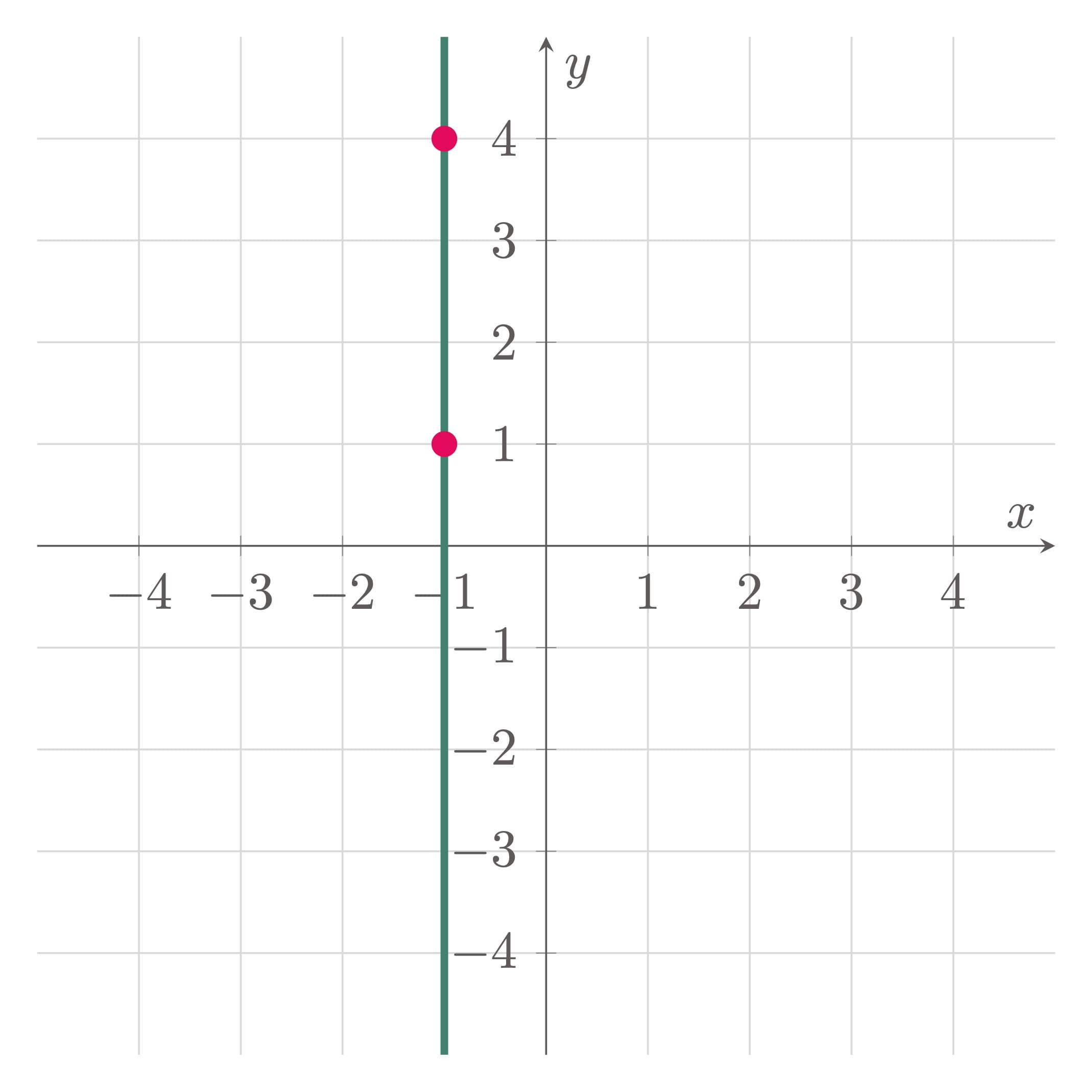
$\example{5}$ Determine the slope of the line that passes through the points $(-1,4)$ and $(-1,1)$. Graph the line.
$\solution$
To solve for the slope use Equation \ref{eq:slope formula}
\[\begin{align*} m &= \frac{y_2-y_1}{x_2-x_1} \\ &= \frac{-1-4}{-1-(-1)} \\ &= \frac{-5}{0} \\ &= \text{undefined} \tagans \end{align*}\]Hence, the line is vertical.