In this lesson, we will begin by defining scalars and vectors. Scalars are quantities that can be characterized solely by their magnitude, whereas vectors are quantities that can be described by their magnitude as well as their direction. For instance, mass, time, and temperature quantities may be entirely represented using only their value alongside their unit; thus, they can be referred to as scalar quantities. On the other hand, because displacement, velocity, acceleration, and force all require an indication of their direction, they can be considered vector quantities.
In our future lessons, we will be encountering more of these quantities. However, in this chapter, we are more concerned with establishing the difference between scalar and vector quantities. Furthermore, we will learn how to combine multiple vector quantities, putting our knowledge in Trigonometry to the test.
Vectors
Vector quantities are usually denoted by a letter or a symbol with an arrow above it, for example, $\vv{A}$ (see Figure 1). Additionally, a vector’s visual representation is an arrow pointing in the direction of its end position. For instance, vector A has an initial position at $P_1$ and has a final position at $P_2$.
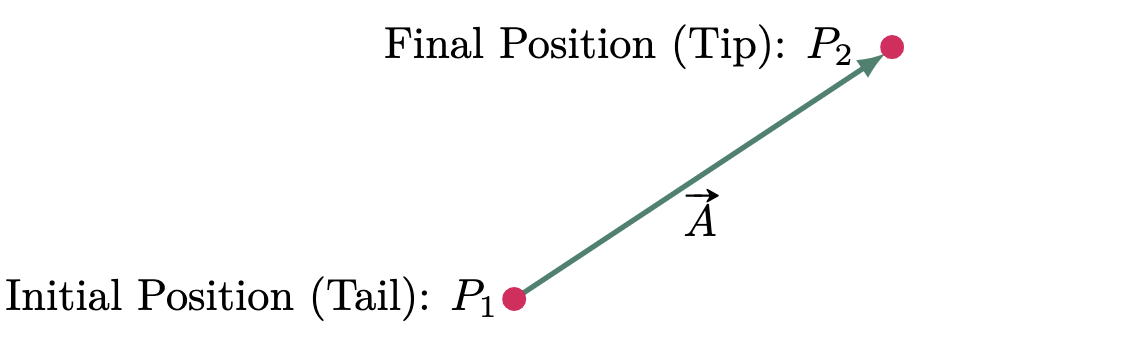
Figure 1: Visual representation of a vector
Magnitude of a Vector
A vector’s magnitude is defined as the length between its initial and final points. As a result, it is a scalar quantity that is unconcerned about its direction. With this in mind, its value will always be positive. To determine the magnitude, we only need to get the absolute value of the vector. The magnitude of a vector is typically denoted by the same letter or symbol of the vector but without the arrow at the top. Hence,
$$\begin{align} \text{Magnitude of }\vv{A}=|\vv{A}|=A \end{align}$$
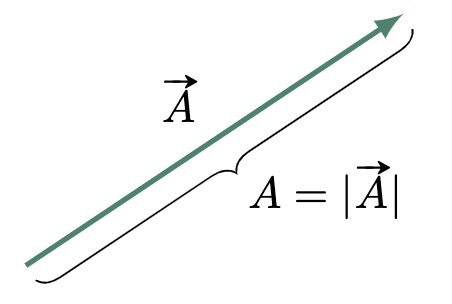
Figure 2: Magnitude of a vector is equal to its length

