Before we can learn how to add and subtract vectors, we must first familiarize ourselves with some of the common types of vectors. Therefore, in this section, we will explore only a few of its types that can help us better understand how vectors work.
Equal Vectors
Vectors with the same magnitude and direction are considered equal regardless of their location. Thus, even if their start and end positions differ, they are still deemed equal as long as their attributes remain unchanged. With this in mind, we can reposition vectors without affecting their value.
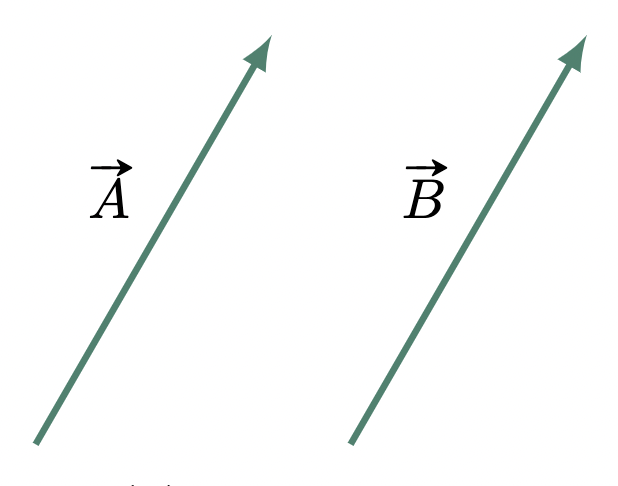
Figure 1: Equal vectors
Negative of a Vector
If two vectors have the same magnitude but opposite in direction, one vector is the negative vector of the other. In Figure 2, vector $\vv{B}$ is equal to the negative of vector $\vv{A}$, $\vv{B}=-\vv{A}$, or vice versa $\vv{A}=-\vv{B}$.
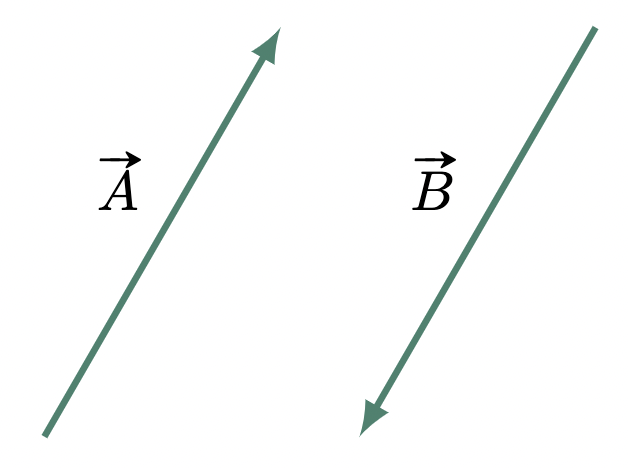
Figure 2: Negative of a vector
Vector Addition
The addition of vectors is not as straightforward as adding scalar quantities. For us to fully grasp the concept, let us have an example. Say a man walks $7\un{m}$ to the right, then $5\un{m}$ to the opposite direction (see Figure 3), the total distance (scalar) traveled by the man is $5\un{m} + 7\un{m} = 12 \un{m}$, but its displacement (vector) is $2\un{m}$ to the right. Note that the direction of the resultant vector points the object’s initial position to its final position.
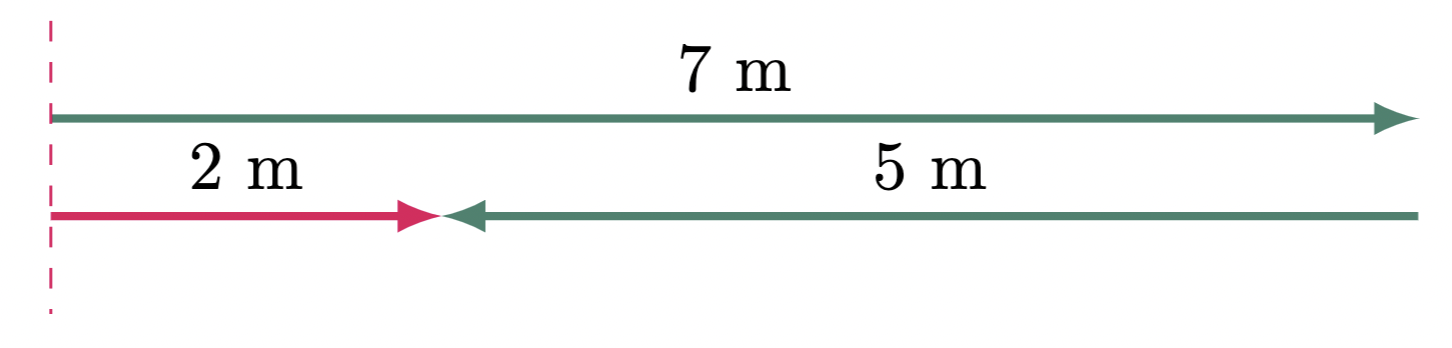
Figure 3: Addition of parallel vectors
On the other hand, to add vectors that are not parallel to one another, we will need some trigonometry skills. However, in this lesson, we will concentrate on its graphical representation in order to visualize the vectors before attempting to solve such problems.
Consider Figure 4a, if we are to find the sum of the two vectors, $\vv{A}+\vv{B}$. We can solve it by placing the tail of vector $\vv{B}$ at the tip of the vector $\vv{A}$ (Figure 4b), then connecting the tail of $\vv{A}$ to the tip of $\vv{B}$; thus, giving us a resulting vector $\vv{R}$, which we now call the vector sum or the resultant. We would also arrive at the same results even if we reverse the order (Figure 4c). Furthermore, we could also add the vectors by constructing a parallelogram (Figure 4d).
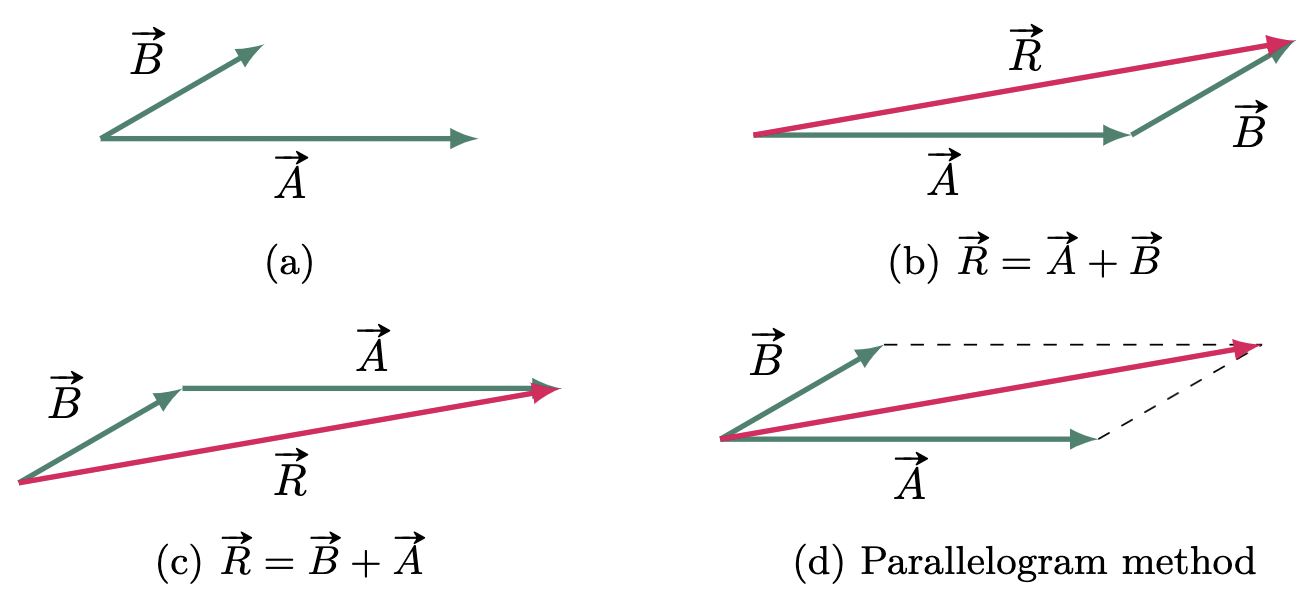
Figure 4: Addition of two non-parallel vectors
This method can also be used when there are more than two vectors involved, and the order of the vectors would still not matter (Figure 5) $\vv{R}=\vv{A}+\vv{B}+\vv{C}$.
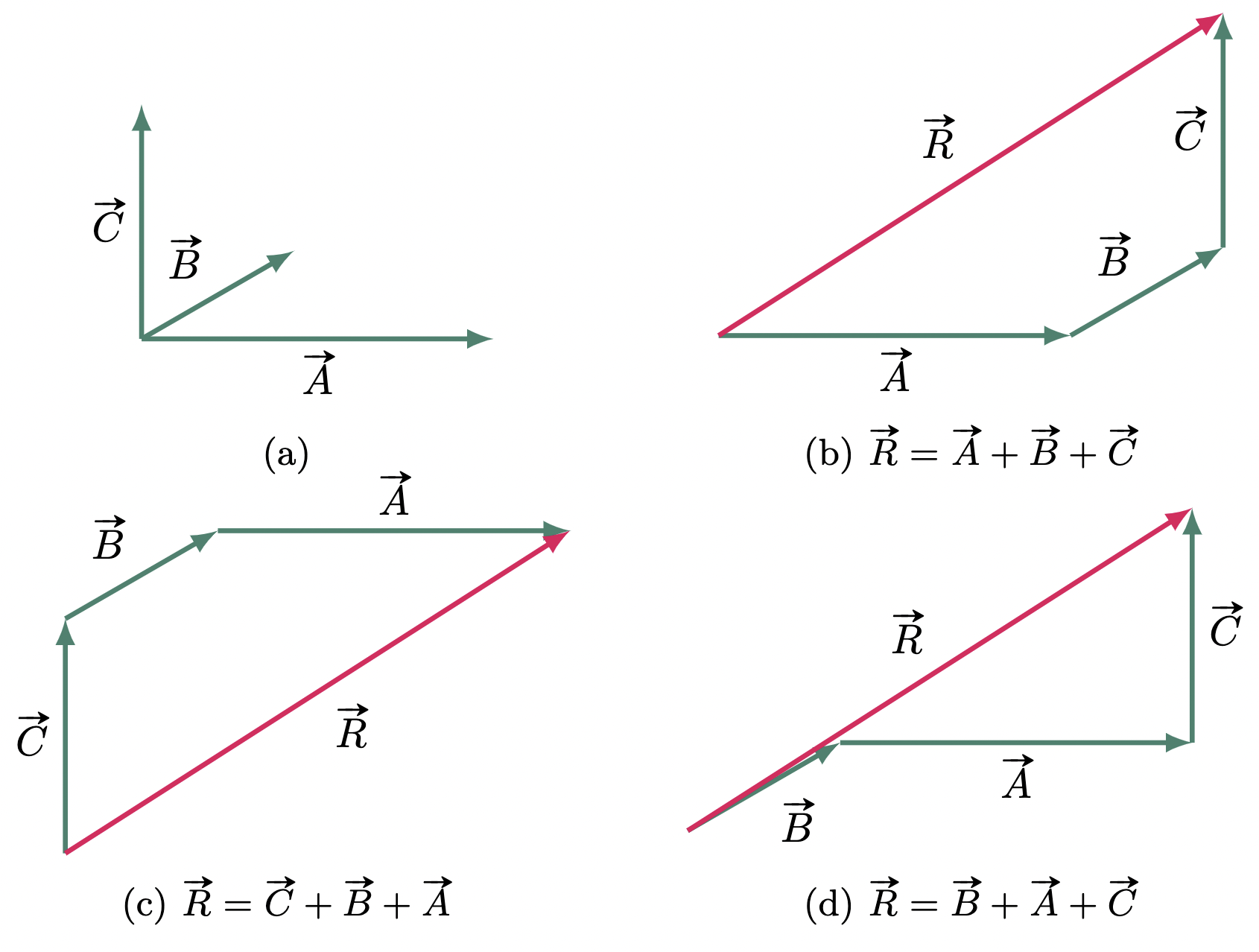
Figure 5: Addition of three non-parallel vectors
Vector Subtraction
In subtracting vectors, say if we are to find the resultant of $\vv{A}-\vv{B}$ (Figure 6). Bear in mind that getting the negative of a vector causes it to point in the opposite direction. Thus, by finding the negative of the subtrahend, we may now add the vectors rather than subtract them.
\[\begin{align*} \vv{R} &= \vv{A}-\vv{B} \\ &= \vv{A}+(-\vv{B}) \end{align*}\]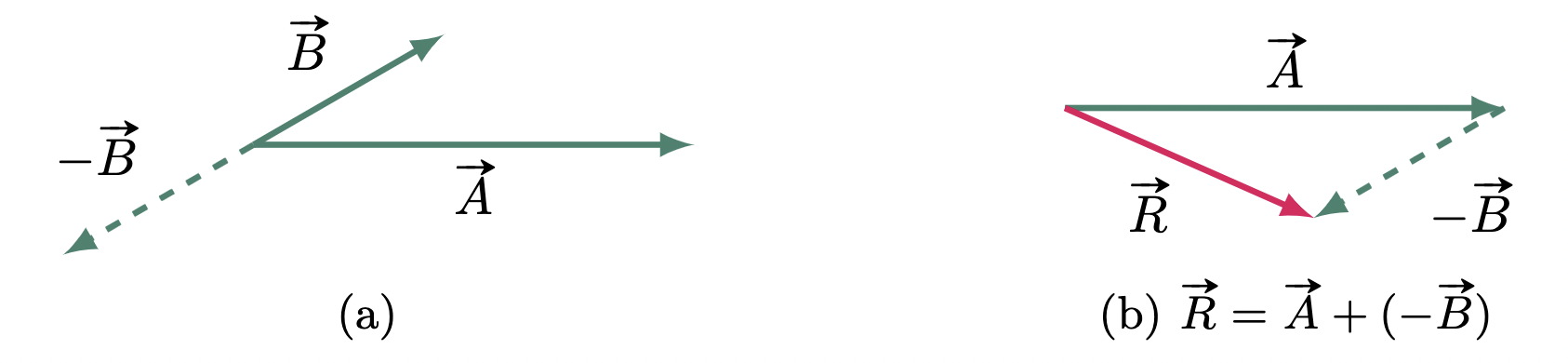
Figure 6: Addition of negative of a vector
$\example{1}$ A man drove 3 km to the east then 5 km to the north. Determine how far and in what direction is he from the starting point.
$\solution$
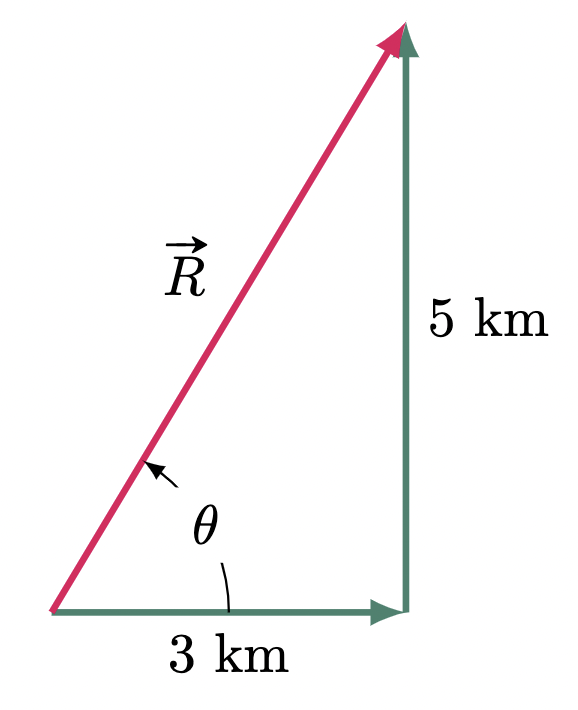
Since the two vectors form a right angle with each other, the resultant can be easily determined by using the Pythagorean Theorem,
\[\begin{align*} R &= \sqrt{(3 \text{ km})^2+(5 \text{ km})^2}\\ &= \sqrt{34 \text{ km}^2} \\ &= 5.83 \text{ km} \tagans \end{align*}\]And for the direction,
\[\begin{align*} \tan\theta &= \frac{\text{opposite}}{\text{adjacent}}=\frac{5\text{ km}}{3\text{ km}}\\ \theta &= \tan^{-1} \br{ \frac{5\text{ km}}{3\text{ km}} } \\ &= 59.04 ^{\circ} \tagans \end{align*}\]Since the angle is measured from east towards north, $\theta=59.04 ^{\circ}$ north of east. Hence the magnitude and direction of the resultant is 5.83 km at $59.04 ^{\circ}$ N of E.
$\example{2}$ Given two vectors $\vv{A}$ and $\vv{B}$, find $\vv{A}-\vv{B}$.
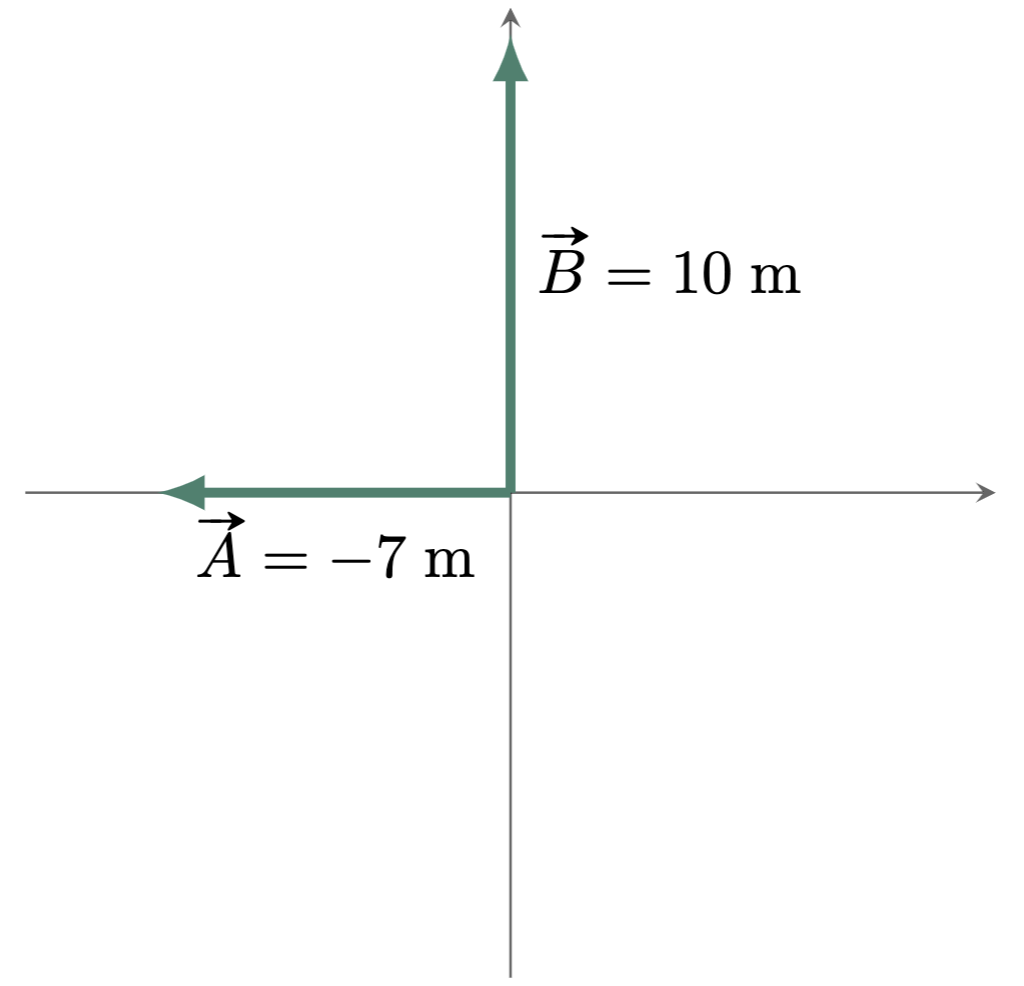
$\solution$
In this example, since we will be subtracting vectors, the first step the we need to do is reverse the direction of the negative vector. In this case,
\[\begin{align*} R &= \vv{A}-\vv{B} \\ &= \vv{A}+(-\vv{B}) \end{align*}\]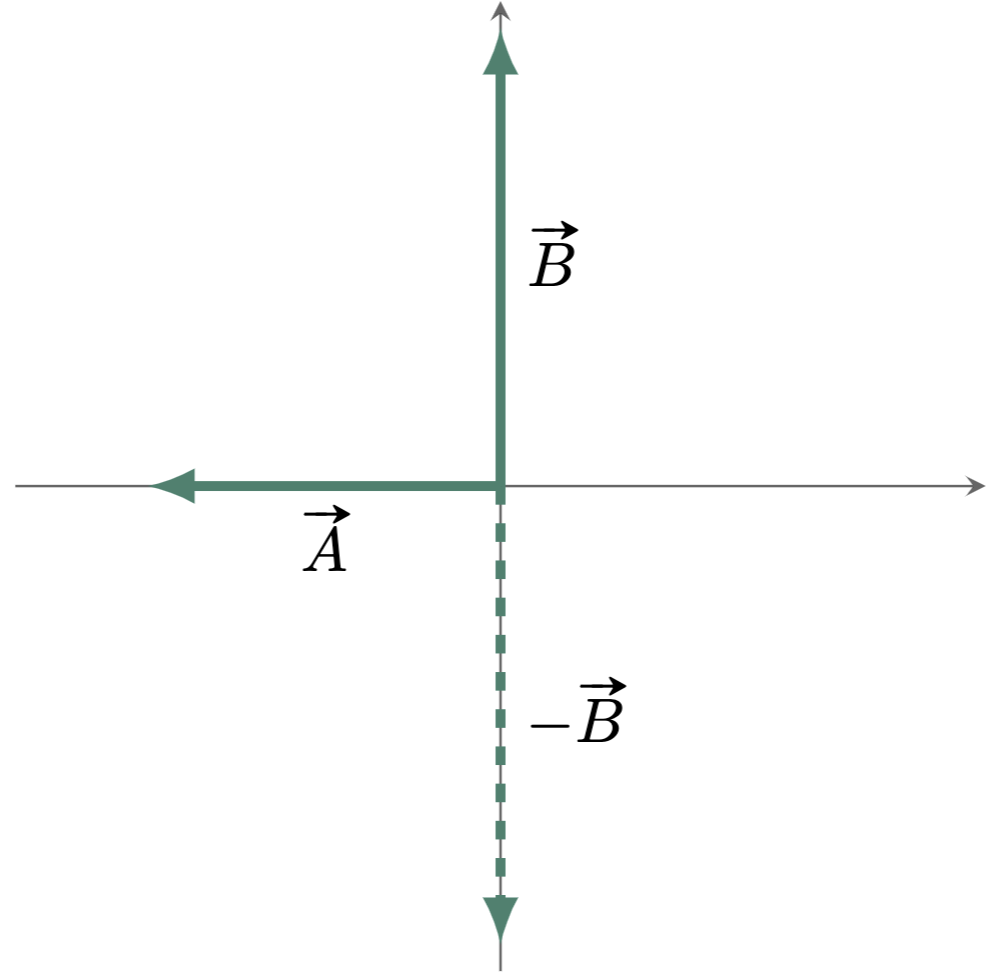
Then Solving for the magnitude of the resultant gives us,
\[\begin{align*} R &= \sqrt{(-7 \un{m})^2+(-10 \un{m})^2}\\ &= \sqrt{149 \un{m}^2} \\ &= 12.21 \un{m} \tagans \end{align*}\]And for the direction,
\[\begin{align*} \tan\theta &=\frac{-10\un{m}}{-7\un{m}}\\ \theta &= \tan^{-1} \br{ \frac{-10\un{m}}{-7\un{m}} } \\ &= 55.01 ^{\circ} \end{align*}\]However, keep in mind that in a Cartesian Plane, angles are often measured from the positive $x$-axis. Thus, we should add $180\degg$ to the solved angle.
\[\begin{align*} \theta &= 180\degg + 55.01\degg \\ &= 235.01 \degg \tagans \end{align*}\]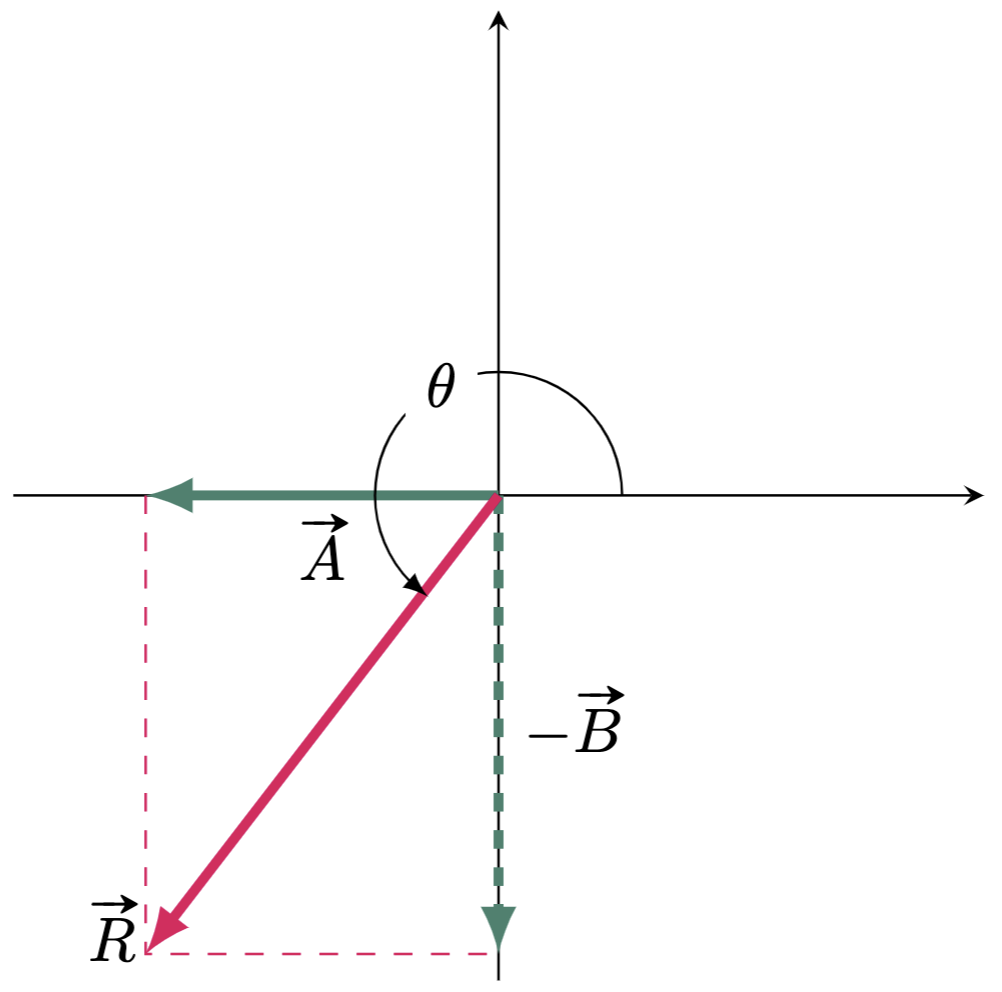
Suppose you’re still wondering why we adjusted the angle and whether it had an effect on the value of the final answer. The answer is, of course, no! Try solving for the values of $\tan(55.01\degg)$ and $\tan(235.01\degg)$. Just make sure that your calculator is set in degrees mode. As you may have seen, the output of the two functions is identical. Hence, adjusting our angle from 55.01 to 235.01 degrees will not affect the value of our final answer.
Therefore, the resultant of $\vv{A}-\vv{B} = 12.21 \un{m}$ with an angle of $235.01\degg$

