From the previous section, we have tried to solve some problems involving vector addition and subtraction. However, we were restricted with either parallel or perpendicular vectors since we can easily apply the Pythagorean Theorem to such problems. More often than not, we will find ourselves solving problems that don’t fit such a situation. Hence, it is best that we must learn how to break down vectors into manageable components.
A vector that lies on a cartesian plane that’s neither horizontal nor vertical can be broken down into two vectors. Consider Figure 1, vectors $\vv{A_x}$ and $\vv{A_y}$ are the component vectors of vector $\vv{A}$. This can also be interpreted as the sum of the component vectors, which equals to $\vv{A}$.
If we are to look at this from a different perspective, we have just reversed the process of adding perpendicular vectors. Thus, rather than obtaining the resultant, the resultant is given, and the components are the two vectors to be added.
$$\begin{align} \vv{A}=\vv{A_x}+\vv{A_y} \end{align}$$
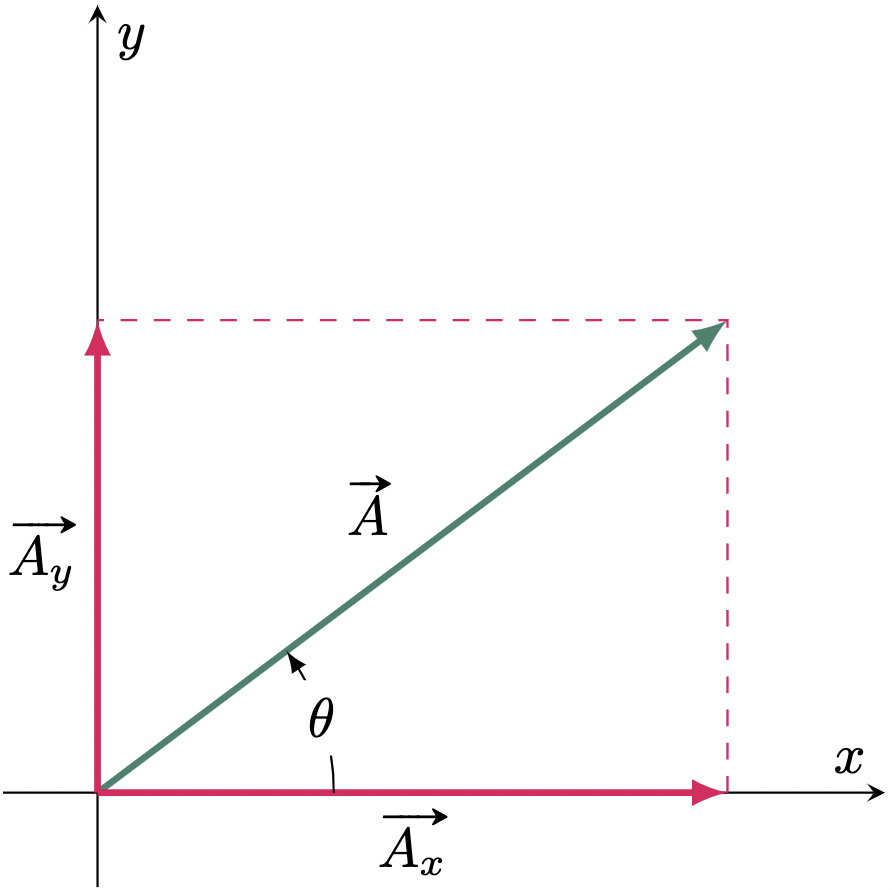
Figure 1: Component vectors of $\vv{A}$
Solving for the components of a vector is relatively simple. All we need is some basic Trigonometry. If you could recall the mnemonic SOH-CAH-TOA, which is denoted as,
\[\begin{align*} \sin\theta &= \ufrac{opposite}{hypotenuse}=\frac{A_y}{A} \\ \cos\theta &= \ufrac{adjacent}{hypotenuse}=\frac{A_x}{A} \\ \tan\theta &= \ufrac{opposite}{adjacent}=\frac{A_y}{A_x} \end{align*}\]Given the magnitude and the direction $\theta$ of a vector, we can solve its $x$ and $y$ components by,
\[\begin{align*} \cos\theta& =\frac{A_x}{A} & \sin\theta &= \frac{A_y}{A} \\ A_x &= A\cos\theta & A_y &= A\sin\theta \end{align*}\]$$\begin{align} & \text{$x$-component:} & A_x &= A\cos\theta \\ & \text{$y$-component:} & A_y &= A\sin\theta \end{align}$$
given that $\theta$ is measured from the $+x$-axis in a counter-clockwise direction.
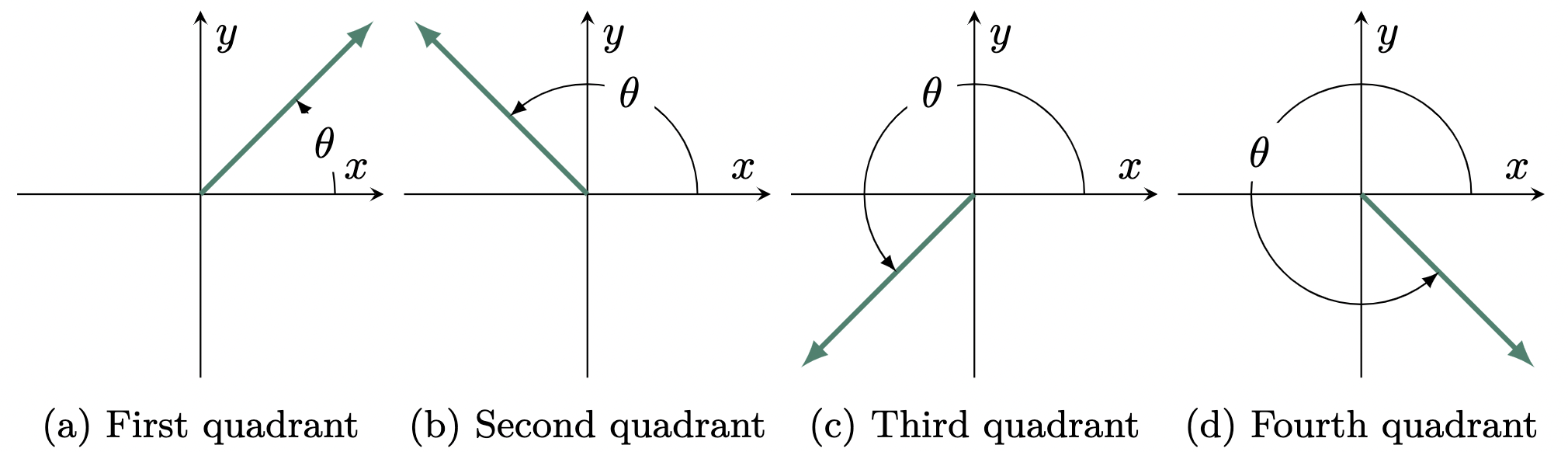
Figure 2: Angle $\theta$ measured from the $+x$-axis in a counter-clockwise direction
$\example{1}$ Determine the $x$ and $y$ components of:
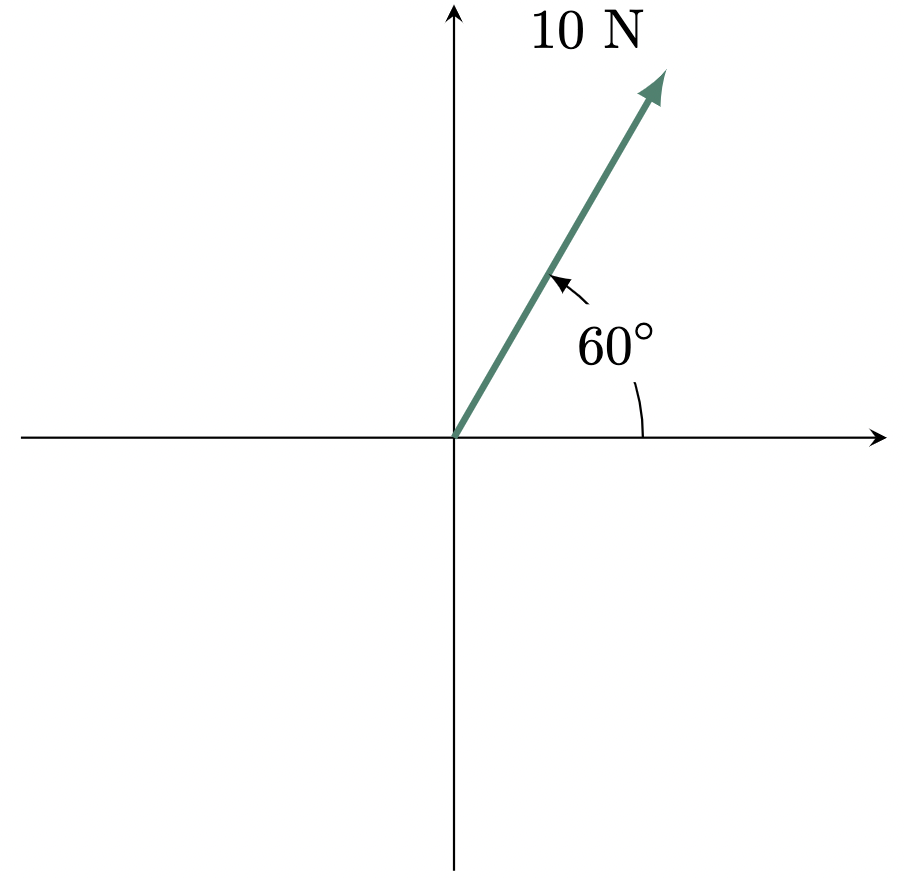
$\solution$
For the $x$-component,
\[\begin{align*} A_x &= A\cos\theta \\ &= 10\text{ N} (\cos{60\degg})\\ &= 5 \text{ N} \tagans \end{align*}\]For the $y$-component,
\[\begin{align*} A_y &= A\sin\theta \\ &= 10\text{ N} (\sin{60\degg)}\\ &= 8.66 \text{ N} \tagans \end{align*}\]$\example{2}$ Determine the magnitude and direction of $\vv{A}+\vv{B}$, if $\vv{A}=15$ N and $\vv{B}=10$ N.
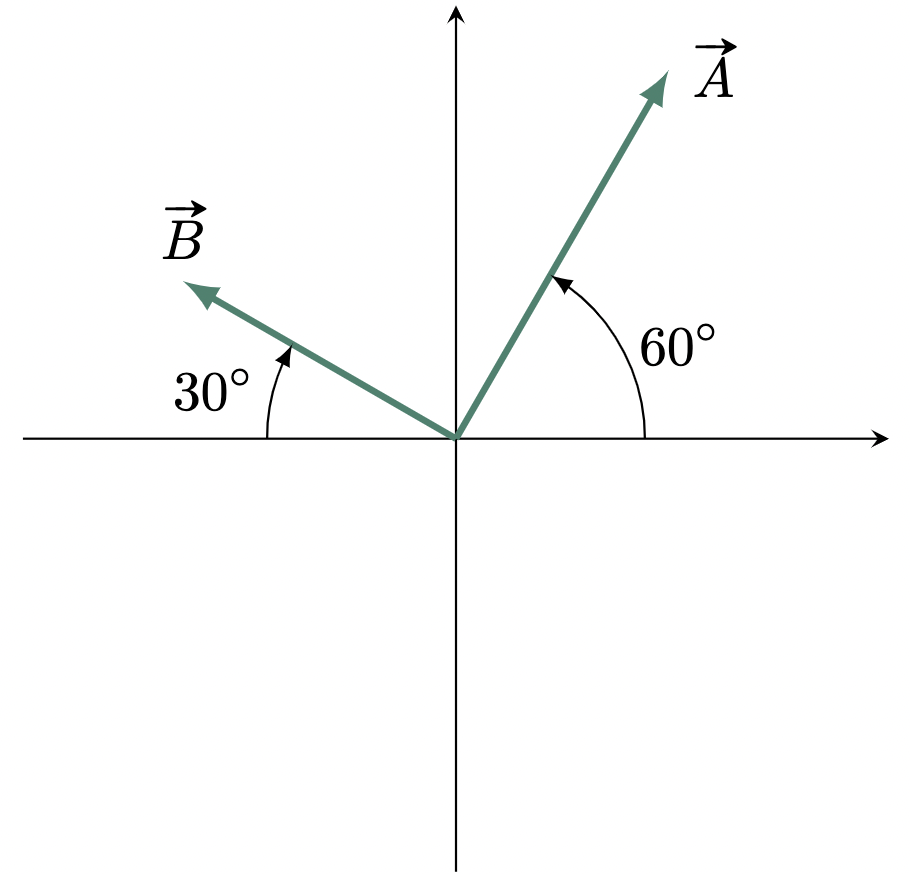
$\solution$
Since the angle must be measured from the positive $x$-axis, the angle of vector $\vv{B}$ is,
\[\begin{align*} \theta_B &= 180\degg-30\degg \\ &= 150\degg \end{align*}\]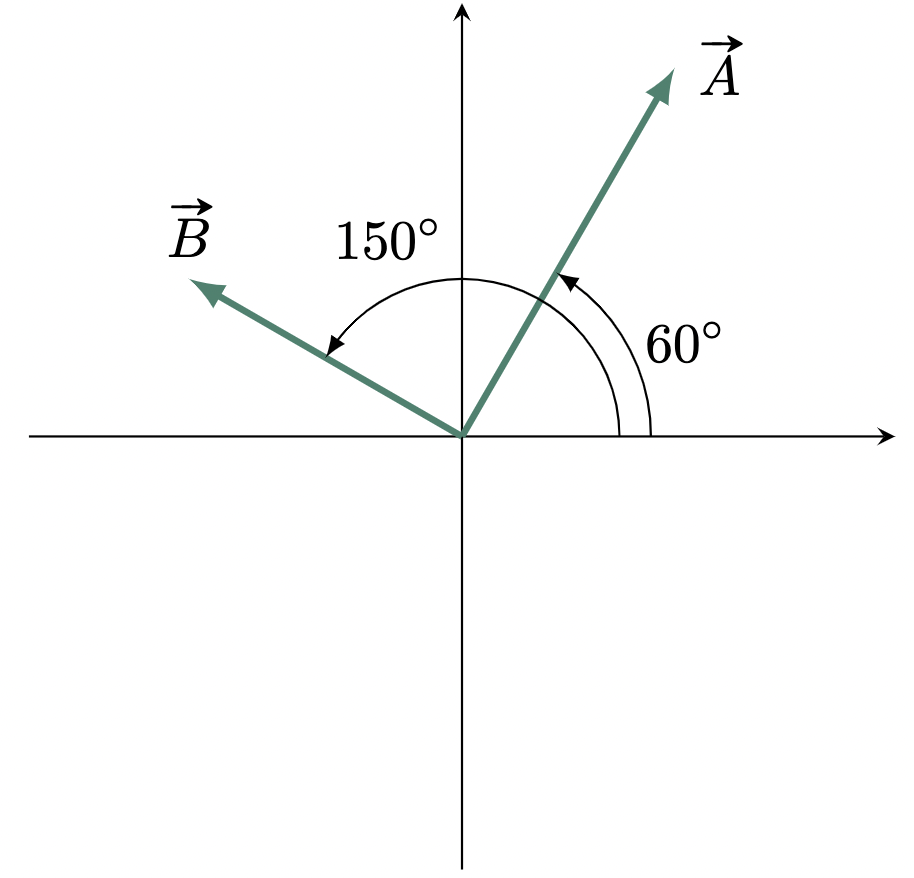
Then solve for the $x$ and $y$ components of the two vectors,
\[\begin{align*} A_x &= A\cos\theta &A_y &= A\sin\theta \\ &= 15\text{ N} (\cos 60\degg) & &= 10\text{ N} (\sin 60\degg) \\ &= 7.5 \text{ N} & &= 12.99 \text{ N} \\ \\ B_x &= B\cos\theta &B_y &= B\sin\theta \\ &= 10\text{ N} (\cos 150\degg) & &= 10\text{ N} (\sin 150\degg)\\ &= -8.66 \text{ N} & &= 5 \text{ N} \end{align*}\]Add the $x$-components of the two vectors to get the $x$-component of the resultant,
\[\begin{align*} R_x &= A_x+B_x\\ &= 7.5 \text{ N} + (-8.66\text{ N})\\ &= -1.16\text{ N} \end{align*}\]Similarly for the $y$-component,
\[\begin{align*} R_y &= A_y+B_y\\ &= 12.99 \text{ N} + 5\text{ N} \\ &= 17.99\text{ N} \end{align*}\]Then add the component vectors of the resultant. Bear in mind that since we will be adding two vectors that are perpendicular to each other, we’ll use the Pythagorean Theorem.
\[\begin{align*} \vv{R} &= \vv{R_x}+\vv{R_y} \\ R &= \sqrt{(R_x)^2+(R_y)^2} \\ &= \sqrt{(-1.16\text{ N})^2+(17.99\text{ N})^2}\\ &= 18.02 \text{ N} \end{align*}\]And for the direction,
\[\begin{align*} \tan\theta_R &= \frac{R_y}{R_x} \\ \theta_R&= \tan^{-1}\br{ \frac{17.99 \text{ N}}{-1.16\text{ N}} } \\ &= -86.31\degg % &= 93.68\degg \end{align*}\]But as you can see, the tip of the resultant vector lies on the second quadrant, but $-86.31\degg$ is at the fourth quadrant. As you may recall on your Trigonometry class, in both the second and fourth quadrant the tangent function is negative. In order to fix this, let’s add $180\degg$ to the angle $-86.31\degg+180\degg = 93.69\degg$. With this in mind, sketching the graph beforehand is very important to be able to predict the direction of the resultant vector.
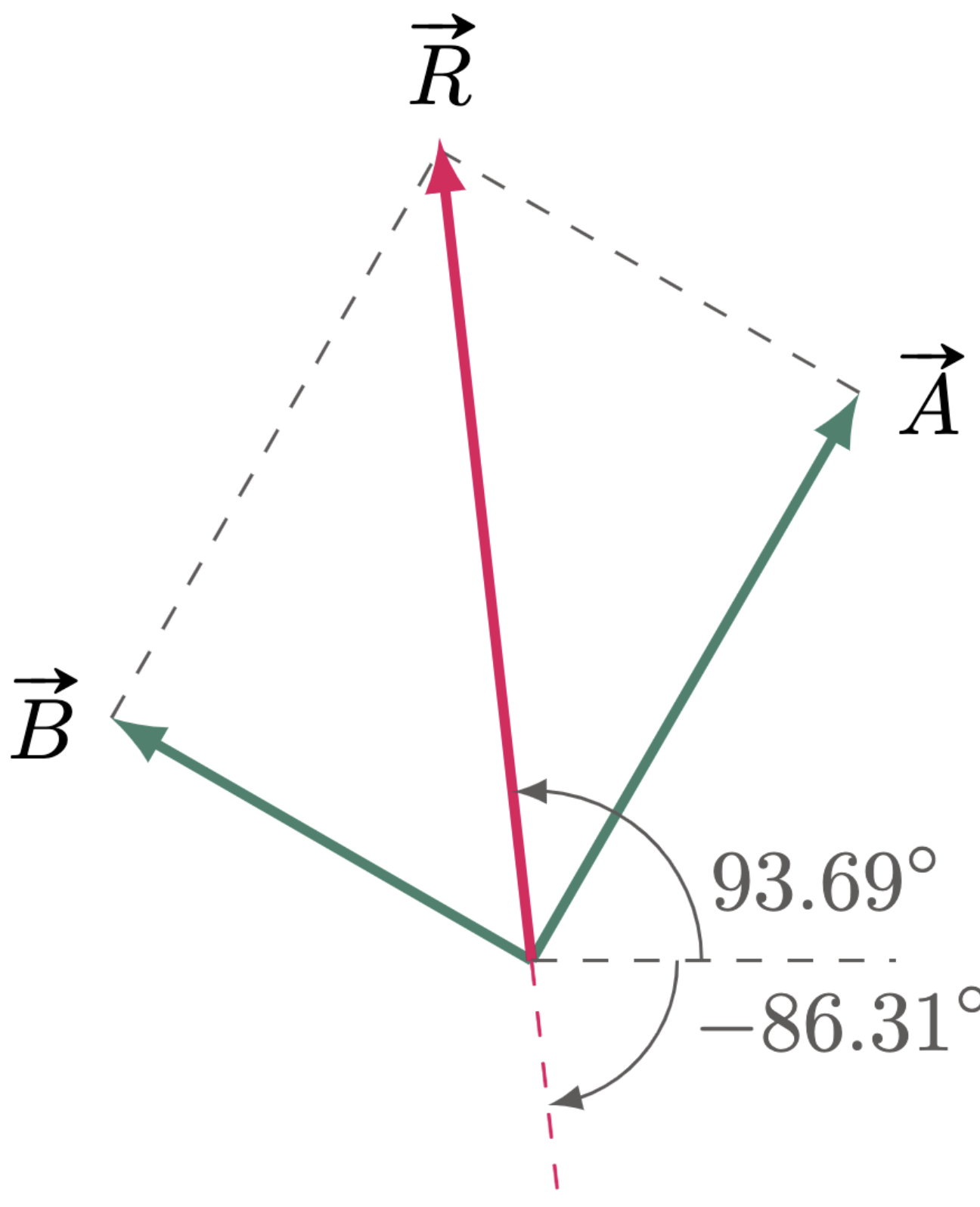
Hence, the magnitude and direction of the resultant is 18.02 N at $93.69\degg$
$\example{3}$ Vector $\vv{A}$ has an $x$-component of $-32.0$ m and makes an angle of $19\degg$ clockwise with the negative $y$-axis. Determine the magnitude of the vector.
$\solution$
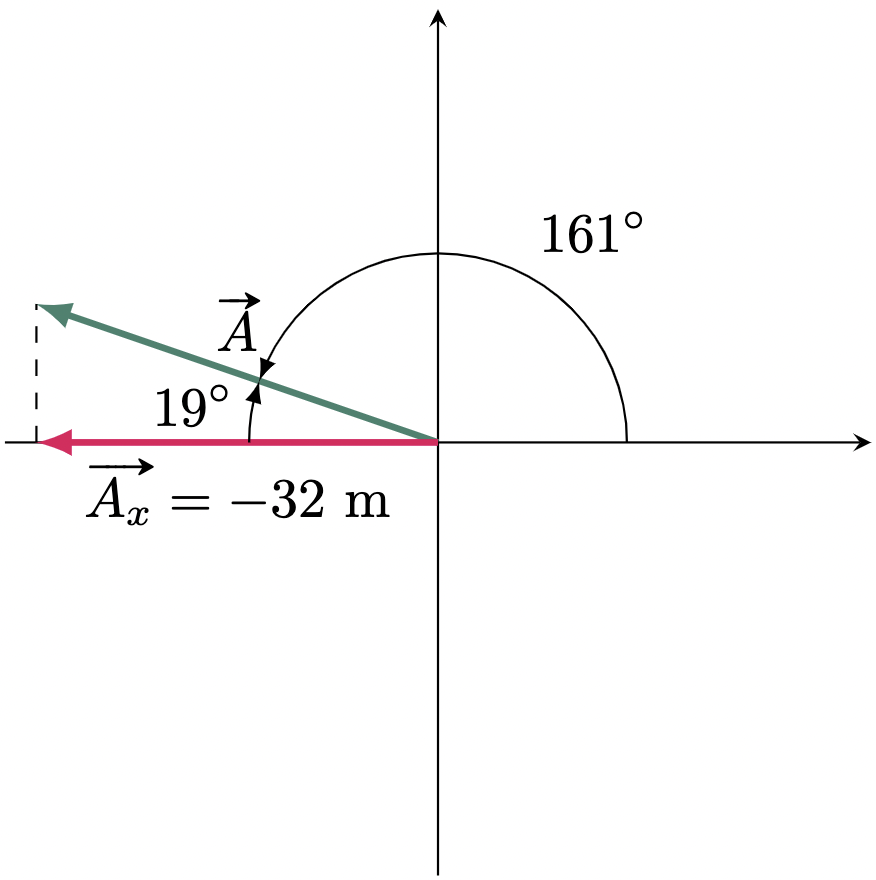
Since we’re required to find the vector $\vv{A}$ (hypotenuse), with a given $x$-component $\vv{A_x}$ (adjacent) and the angle $\theta$, we can use the cosine function,
\[\begin{align*} \cos\theta &= \frac{A_x}{A} \\ A &= \frac{A_x}{\cos\theta} \\ &= \frac{32.0 \text{ m}}{\cos 19\degg} & &&= \frac{-32.0 \text{ m}}{\cos 161\degg} \\ &= 30.25 \text{ m} &\text{or}& &= 30.25 \text{ m} \tagans \end{align*}\]
