Electrostatic Force is the force of either attraction or repulsion experienced by two charged particles. This force is also called the Coulomb Force or Coulomb Interaction. Several factors affect the strength of the force between the charges, such as the magnitude of the particles’ charge and the distance between them.
Also, the direction of the forces will depend on the sign of the charges. As we have learned from the previous lesson, opposite charges attract, and like charges repel.
Experiments have shown that the distance between the charges hugely affects the force between them.
And this leads to what is known as Coulomb’s Law, which is denoted as,
$$\begin{align} F=k\frac{|q_1||q_2|}{r^2} \end{align}$$
\(\begin{align*} \text{Where: } \quad F &= \text{Electrostatic Force} & \\ |q_1| &= \text{magnitude of one particle} \\ |q_2| &= \text{magnitude of the other particle} \\ r &= \text{distance between the two particles} \\ k &= \text{proportionality constant} \\ &= 8.99\times 10^9 \un{N\frac{m^2}{C^2}} \end{align*}\)
The resulting force using Coulomb’s Law does not give the direction. Its direction will either go towards or away from each other, depending on the charges’ sign.
With this in mind, the force’s magnitude will not be affected by the sign of the charges.
Consider $\fref{1}$, in both (a) and (b), $q_1$ and $q_2$ have the same magnitude, but the only difference is that $q_2$ is negative on (a) and positive on (b). The magnitude of the forces in both (a) and (b) are the same; the only difference is its direction.
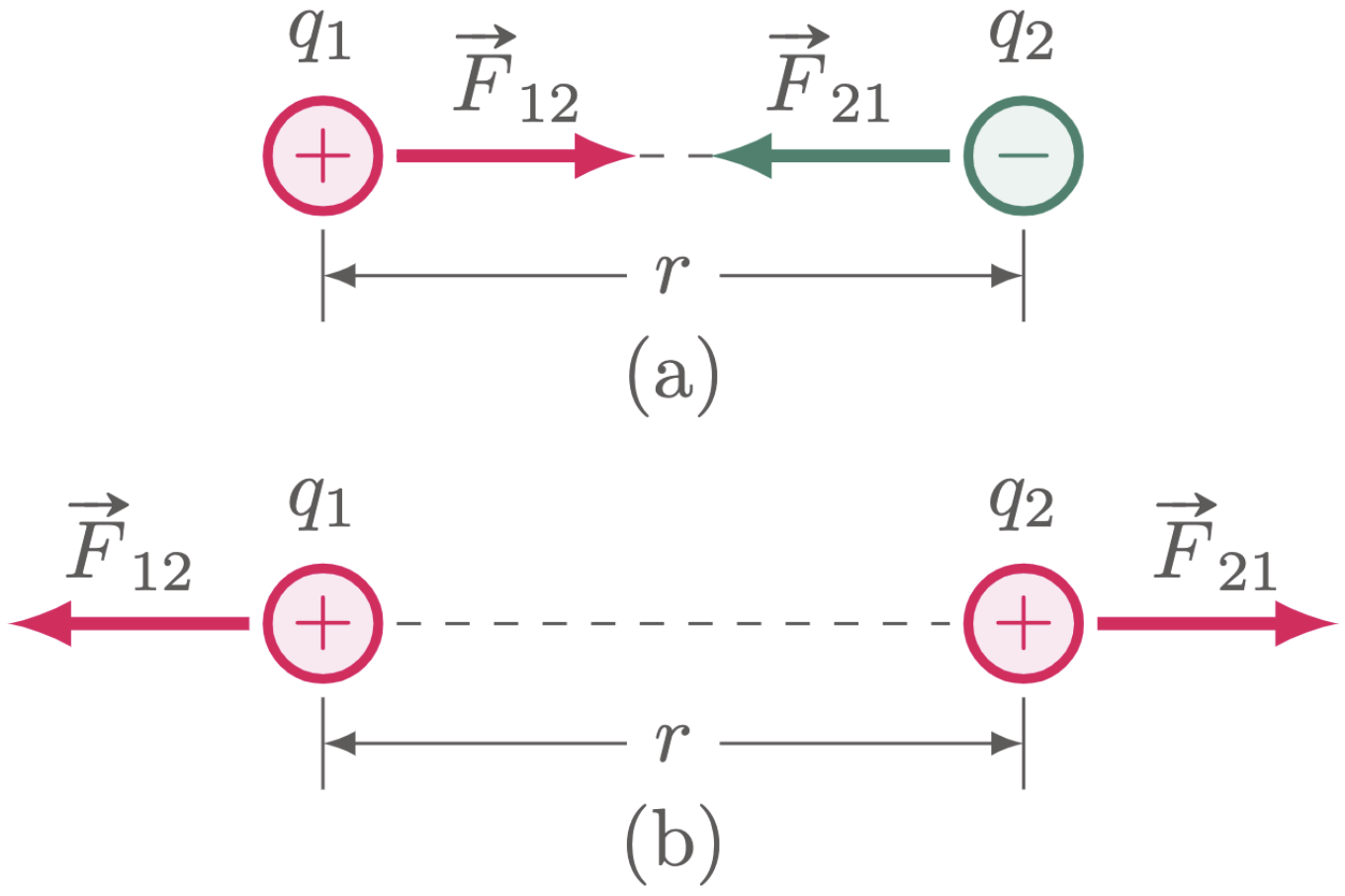
Figure 1: The sign of the charges will determine the direction of the force.
In $\fref{1}$, the subscript “12’’ on $F_{12}$ represents the force exerted by particle 2 to particle 1. On the other hand, the subscript “21’’ represents the force exerted by particle 1 to particle 2.
$\example{1}$
Two particles are separated at a distance of 1.3 m and have charges of $+27.0 \un{\mu C}$ and $+35 \un{\mu C}$.
(a) What is the magnitude of the force of each particle?
(b) Is the force attractive or repulsive?
$\given$
\(\begin{align*}
q_1 &= 27\un{\mu C} = 27\x 10^{-6} \un{C} &\\
q_2 &= 35\un{\mu C} = 35\x 10^{-6} \un{C} \\
r &= 1.3\un{m}
\end{align*}\)
$\solution$
$\For{a}$
To determine the force of the particles, we can use the Coulomb’s Law.
Hence, each particle experience a force of $5.03\un{N}$.
$\For{b}$
Since both charges are positive, the force between the two particles is repulsive.
$\example{2}$
Two spheres have charges of $+24.0 \un{\mu C}$ and $-62.0 \un{\mu C}$. They are separated by a distance of 95.0 cm.
(a) What is the magnitude of the force that each sphere experiences,
(b) Is the force attractive or repulsive?
(c) The spheres are brought into contact and then separated to a distance of 95.0 cm. Determine the magnitude of the force that each sphere now experiences, and state whether the force is attractive or repulsive.
$\given$
\(\begin{align*}
q_1 &= 24\un{\mu C} = 24\x 10^{-6} \un{C} &\\
q_2 &= -62\un{\mu C} = -62\x 10^{-6} \un{C} \\
r &= 3.5\un{cm} = 0.95\un{m}
\end{align*}\)
$\solution$
$\For{a}$
Using Coulomb’s Law,
$\For{b}$
Since the sign of the charges are opposite, the force is attractive.
$\For{c}$
When the two spheres are brought to contact, their charges tend to be evenly distributed. With this in mind, we can solve for the charge of each sphere by averaging their charges.
To determine the force after been separated, use Coulomb’s Law,
\[\begin{align*} F &= k\frac{|q_1||q_2|}{r^2} \\ &= 8.99\times 10^9 \un{N\frac{m^2}{C^2}} \cdot\frac{|-19\x 10^{-6} \un{C}||-19\x 10^{-6} \un{C}|}{(0.95\un{m})^2} \\ &= 3.60\un{N} \tagans \end{align*}\]The two spheres both carry negative charges. Hence the force is repulsive.
$\example{3}$ Three point charges are placed at the following points on the $x$-axis: $-4.0 \un{\mu C}$ at $x=0$, $+3.0 \un{\mu C}$ at $x=20\un{cm}$, and $-6.0 \un{\mu C}$ at $x=50\un{cm}$. Determine the net electrostatic force on the $+3.0 \un{\mu C}$ charge due to the two other charges.
$\given$
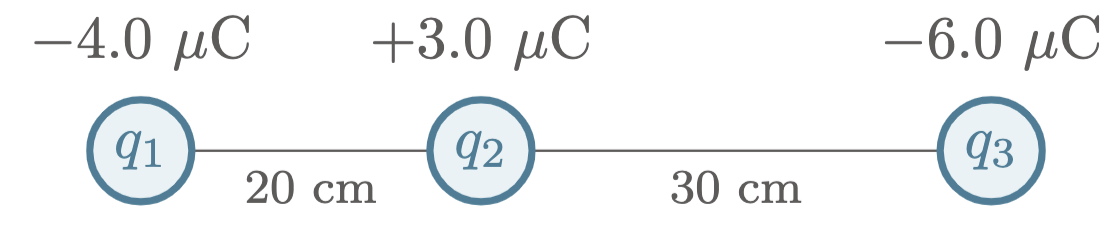
\(\begin{align*} q_1 &= -4.0\un{\mu C} = -4.0\x 10^{-6} \un{C} &\\ q_2 &= +3.0\un{\mu C} = +3.0\x 10^{-6} \un{C} \\ q_3 &= -6.0\un{\mu C} = -6.0\x 10^{-6} \un{C} \\ r_{12} &= 20 \un{cm} = 0.20 \un{m} \\ r_{23} &= 30 \un{cm} = 0.30 \un{m} \end{align*}\)
$\solution$
For this particular example, two charges affect $q_2$. To solve for the net force on $q_2$, we can first solve for the force between $q_1$ and $q_2$, then $q_2$ and $q_3$.
In sketching the Free Body Diagram (FBD) of $q_2$, we can see that $q_1$ and $q_2$ attract each other, and $q_2$ and $q_3$ also attract each other. Hence, the FBD of $q_2$ will look like,
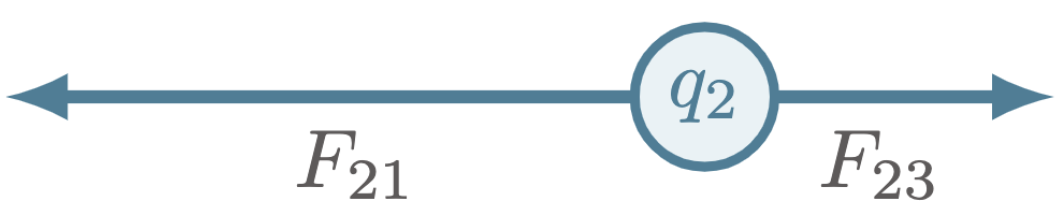
Given that a force is a vector quantity, its direction is critical for calculating the sum of several forces. With this in mind, we may assign the positive $x$ direction (to the right) to be positive. As a result, $F_{23}$ becomes positive, while $F_{12}$ becomes negative. Thus, the net force of $F_{2}$ is,
\[\begin{align*} F_2 &= F_{12}+F_{23} \\ &= (-2.70\un{N})+1.80\un{N} \\ &= -0.9\un{N} \tagans \end{align*}\]The negative sign indicates that the net force is pointing the negative $x$ direction (to the left).
$\example{4}$ In the figure below, three point charges lie in a two-dimensional axis. Determine the magnitude and direction of the net force on $q_1$.
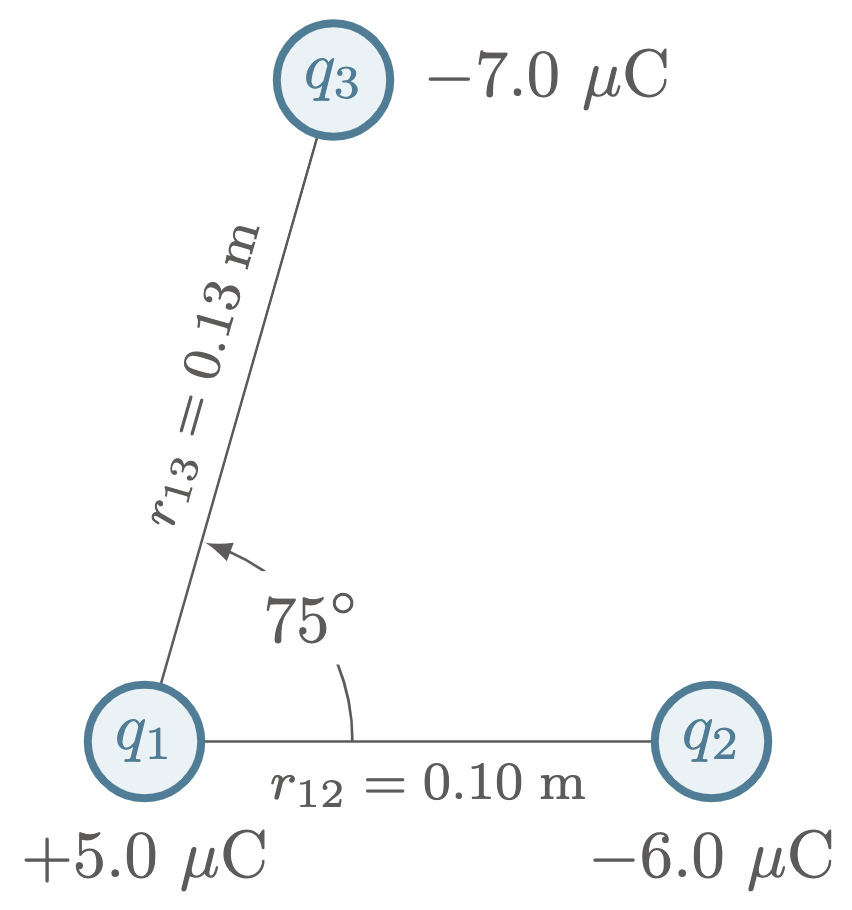
$\given$
\(\begin{align*}
q_1 &= +5.0\un{\mu C} = +5.0\x 10^{-6} \un{C} &\\
q_2 &= -6.0\un{\mu C} = -6.0\x 10^{-6} \un{C} \\
q_3 &= -7.0\un{\mu C} = -7.0\x 10^{-6} \un{C} \\
r_{12} &= 0.10 \un{m} \\
r_{13} &= 0.13 \un{m}
\end{align*}\)
$\solution$
To solve for the net force on $q_1$, we can first solve for the force between $q_1$ and $q_2$, then $q_1$ and $q_3$.
Sketching the FBD of $q_1$,
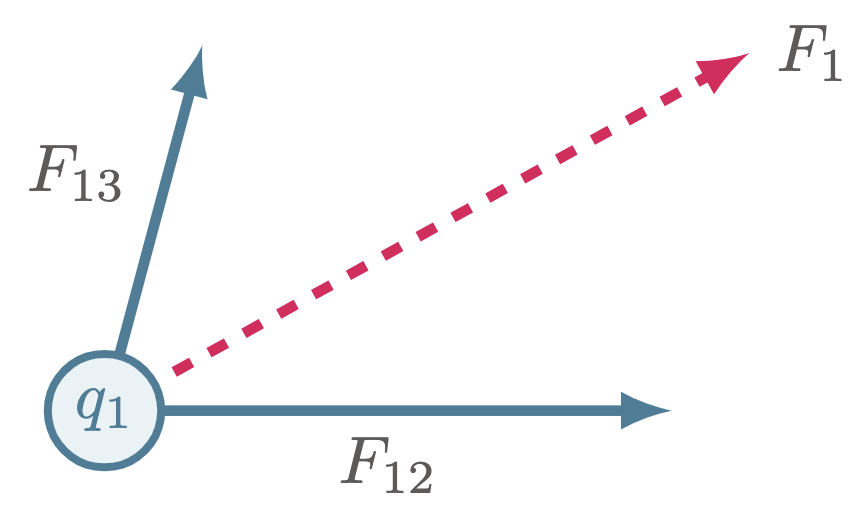
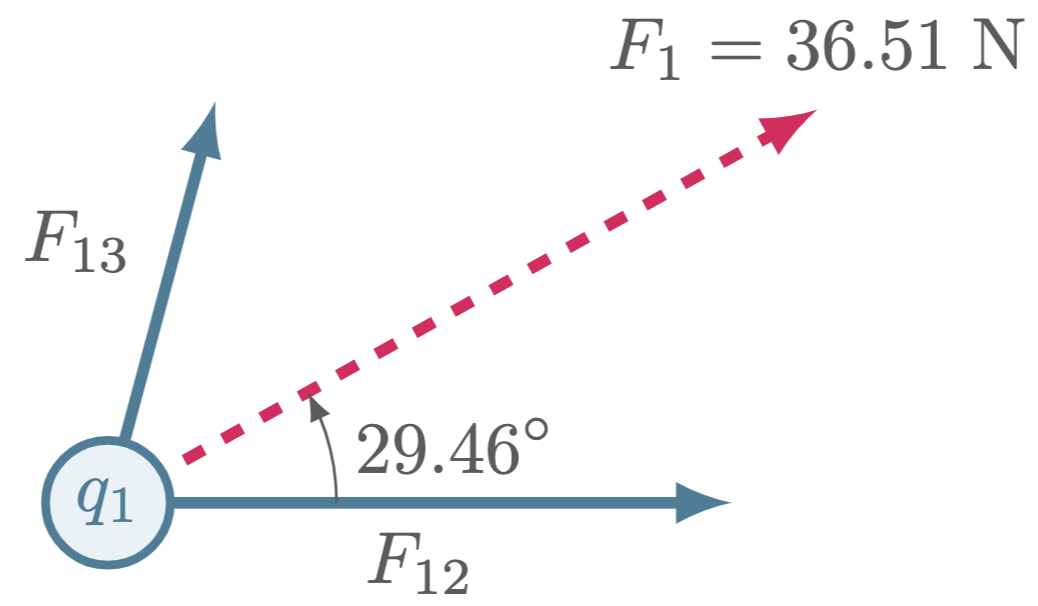
The net force $F_1$ is the vector sum of $F_{12}$ and $F_{13}$. As you may have recalled in the previous semester, there are many methods in solving for the vector sum. But the one that we will be using is the component method, where we would first determine the component vectors for both $F_{12}$ and $F_{13}$
\[\begin{align*} F_{12x} &= F_{12}\cos\theta & F_{12y} &= F_{12}\sin\theta \\ &= 26.97\un{N}(\cos 0\degg) & &= 26.97\un{N}(\sin 0\degg) \\ &= 26.97\un{N} & &= 0\un{N} \\ \\ F_{23x} &= F_{23}\cos\theta & F_{23y} &= F_{23}\sin\theta \\ &= 18.61\un{N}(\cos 75\degg)& &= 18.61\un{N}(\sin 75\degg)\\ &= 4.82\un{N} & &= 17.96\un{N} \end{align*}\]Add the $x$-components of the two vectors to get the $x$-component of the resultant,
\[\begin{align*} F_{1x} &= F_{12x} + F_{23x}\\ &= 26.97\un{N} + 4.82\un{N} \\ &= 31.79\un{N} \end{align*}\]Similarly for the $y$-component,
\[\begin{align*} F_{1y} &= F_{12y} + F_{23y}\\ &= 0\un{N} + 17.96\un{N} \\ &= 17.96\un{N} \end{align*}\]Then add the component vectors of the resultant,
\[\begin{align*} \vv{F_{1}} &= \vv{F_{1x}}+\vv{F_{1y}} \\ F_{1} &= \sqrt{(F_{1x})^2+(F_{1y})^2} \\ &= \sqrt{(31.79\un{N} )^2+(17.96\un{N})^2}\\ &= 36.51\un{N} \tagans \end{align*}\]And for the direction,
\[\begin{align*} \tan\theta_{F_{1}} &= \frac{F_{1y}}{F_{1x}} \\ \theta_{F_{1}}&= \tan^{-1}\br{ \frac{17.96\un{N}}{31.79\un{N} } } \\ &= 29.46\degg \tagans % &= 93.68\degg \end{align*}\]Hence, the magnitude of the force on $q_1$ is $36.51\un{N}$ with a direction of $29.46\degg$ relative to the positive $x$-axis.