Some material or matter allows the flow of electrons among its atom, these materials are called conductors.
When an electron flows, charges also flow. This movement of charges entails energy, and this notion is the fundamental principle of electricity. This flow happens because of the interaction between the positive and negative charges ($\fref{1}$).
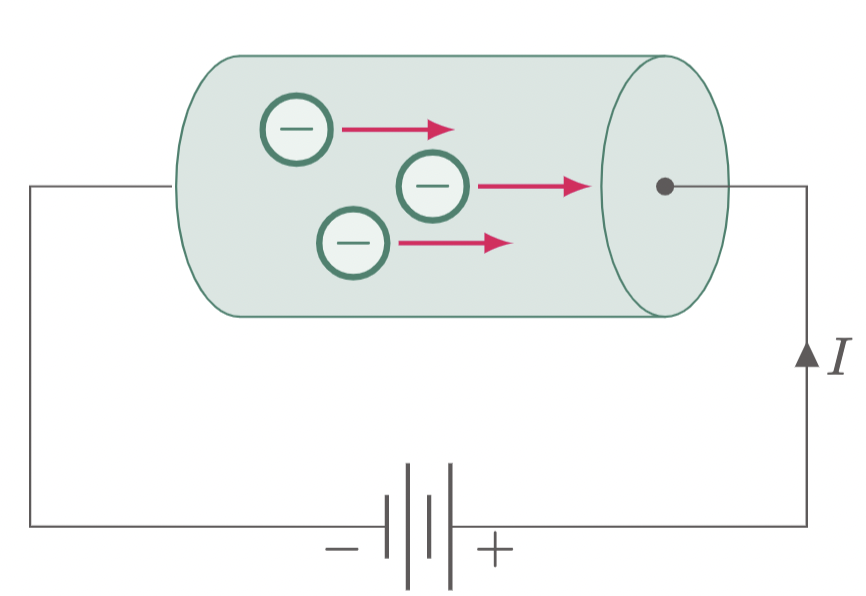
Figure 1: Flow of electrons and current on a closed circuit
The rate of the flow of electrons is called the current, which is denoted by the symbol $I$.
Electric current or simply, current, is defined as the rate of change of charges per unit time, and is measured in amperes [A]. The unit ampere is named after a French Physicist, Andre-Marie Ampere. Mathematically, current is defined as:
$$\begin{align} I = \frac{Q}{t} \label{eq:current in terms of charge and time} \end{align}$$
\(\begin{align*} \text{Where:}\quad I &= \text{current, [A]} & \\ Q &= \text{charge, [C]} \\ t &= \text{time, [s]} \end{align*}\)
Considering $\fref{1}$, the direction of flow of the electron points to the opposite direction of the current $I$. This is so, since before anyone have discovered that electrons are actually the one that flows, it was once believed that the current flow follows the movement of the proton. However, in our lessons, we will be using the conventional flow, which moves from positive to negative.
Direct and Alternating current
The Current being a function of charge is not necessarily a constant-valued function. There can be several types of current, depending on the function of charge per unit time. If the current remains constant, where it does not vary with time, it is called Direct Current ($\fref{2a}$). Moreover, a common time-varying current is the sinusoidal current called Alternating Current ($\fref{2b}$). In this class, we will use the symbol $I$ to represent a constant current, while $i$ will be used to represent a time-varying current.
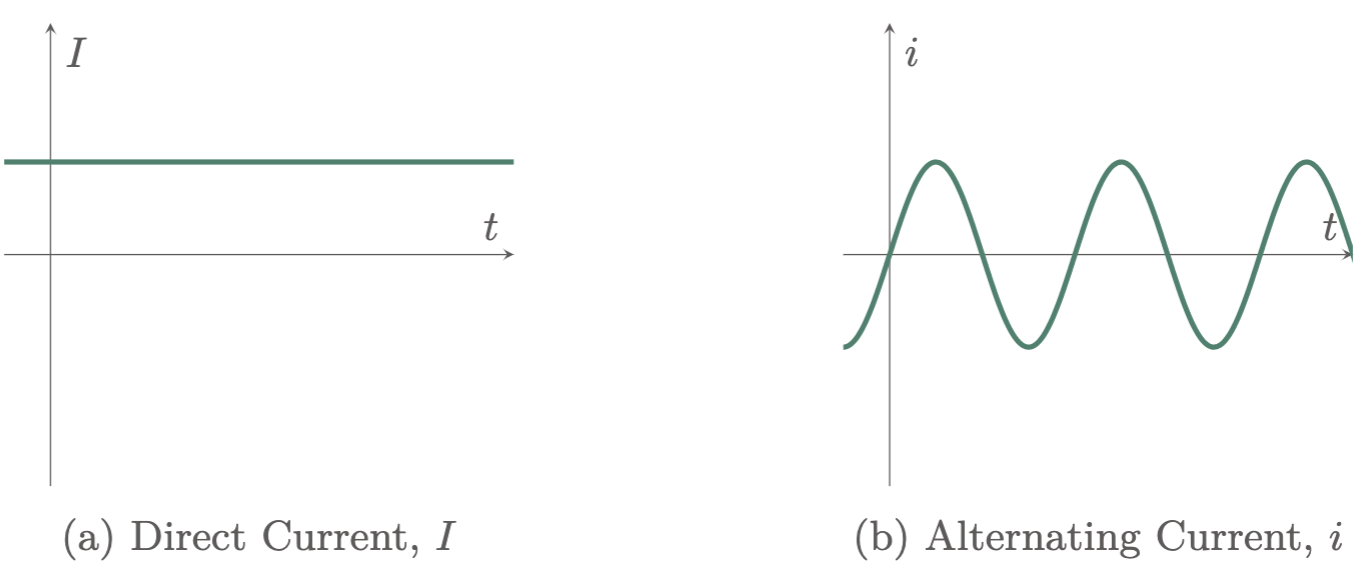
Figure 2
$\example{1}$ How much charge in coulombs is present in an atom with 1200 free electrons?
$\solution$
The magnitude of an elementary charge is $1.602\x 10^{-19}\un{C}$. However, since an electron carries a negative charge, every electron has $-1.602\x 10^{-19}\un{C}$. Hence,
$\example{2}$ A constant current of 0.6 A passes through a wire. Determine the amount of charge that flowed in one minute.
\(\given\)
\(\begin{align*}
I &= 0.6\un{A} & \\
t &= 1\un{min} = 60\un{sec}
\end{align*}\)
$\solution$
To solve for the current, use equation \ref{eq:current in terms of charge and time},
Current Density
The Current Density measures the amount of electric current that flows through a unit area ($\fref{3}$). Current density is a vector quantity, its direction point in the same direction as the current. Mathematically, the magnitude of the current density is defined as,
$$\begin{align} J = \frac{I}{A} \end{align}$$
\(\begin{align*} \text{Where:}\quad J &= \text{current density, [$\mathrm{A/m^2}$]} & \\ I &= \text{current, [A]} & \\ A &= \text{cross-sectional area of the conductor, [$\mathrm{m^2}$]} \end{align*}\)

Figure 3: Current density

