As previously established, electron movement is dependent on two conditions: (a) an electromotive force (voltage) and (b) a closed path. Together with the voltage, the closed path constitutes a complete electrical circuit. A physicist named George Simon Ohm found that current is directly proportional to the provided voltage in an electric circuit and therefore formulated an equation and what is now known as Ohm’s law.
According to Ohm’s law, the voltage $V$ across a resistor is proportional to the current $I$ flowing through it.
\[V \propto I\]Ohm defined the resistance, $R$, as the constant of proportionality for a resistor. $R$ is expressed in ohms, which is indicated by the symbol omega [$\ohm$]. Note that resistance will be explored in greater detail in the following lesson; in the meantime, consider it as a parameter that relates voltage and current.
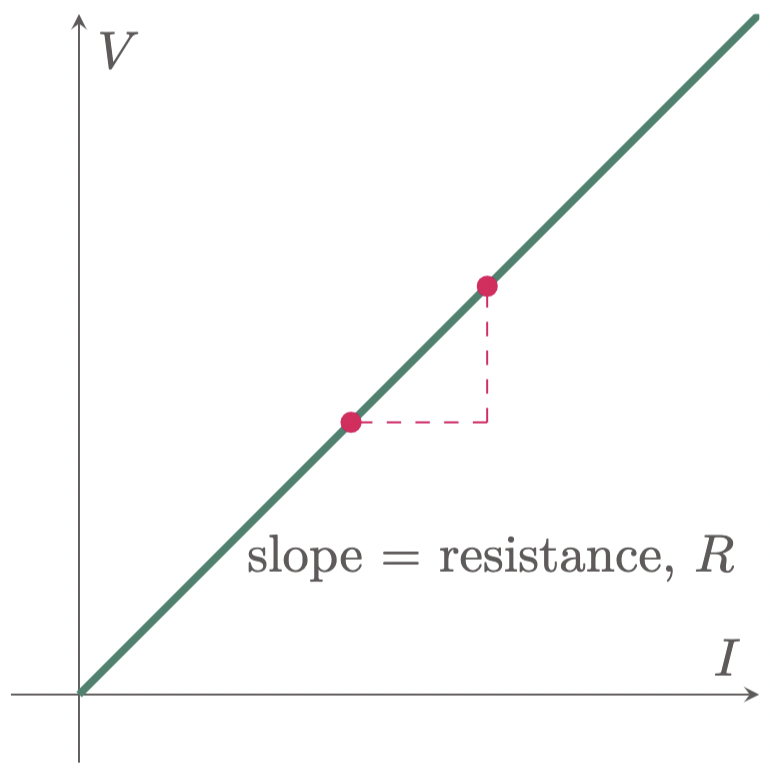
Figure 1: The resistance is equal to the slope of the current-voltage graph.
Mathematically, Ohm’s law can be expressed as:
$$\begin{align} V = IR \end{align}$$
\(\begin{align*} \text{Where:}\quad V &= \text{voltage, [V]} & \\ I &= \text{current, [A]} \\ R &= \text{resistance, [$\ohm$]} \end{align*}\)
$\example{1}$ An electric iron draws 2-A of current. If the iron is known to posses 60 ohms of resistance, find the supplied voltage.
$\given$
\(\begin{align*}
I &= 2\un{A} & \\
R &= 60\un{\ohm}
\end{align*}\)
$\solution$
To solve for the voltage, use the Ohm’s Law,
$\example{2}$ Consider the circuit shown below. Using the Ohm’s law, determine the current that will flow in the circuit when the switch is closed.
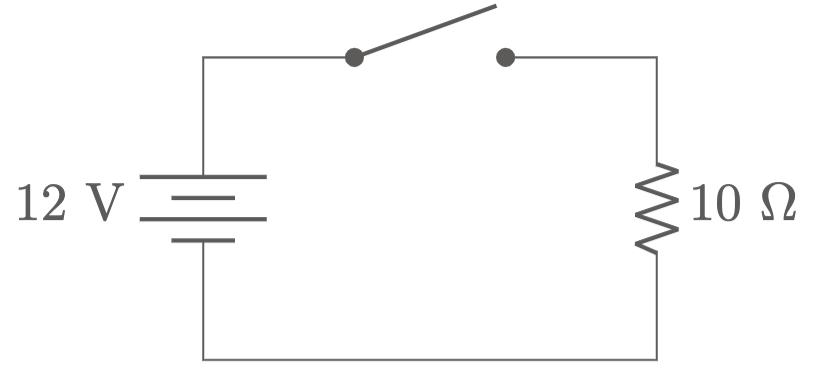
$\given$
\(\begin{align*}
V &= 12\un{V} & \\
R &= 10\un{\ohm}
\end{align*}\)
$\solution$
Consider the following data from the circuit, to calculate the current $I$, use the Ohm’s Law,

