From the previous section, we already discussed the main difference between a scalar and a vector quantity and had some examples regarding this particular topic. To recall, distance is a scalar quantity, and displacement is a vector. Distance refers to “how much ground an object has covered.” While displacement refers to “how far the object is from its starting position,” we could also interpret this as a “change in its position.”
Distance is usually represented by the symbol $s$, and the displacement by the symbol $\vv{s}$. Furthermore, since the displacement measures the change in position, if $s_i$ is the object’s initial position and $s_f$ is the final position, we can denote the displacement as,
$$\begin{align} \mathrm{displacement}=\Delta\vv{s}=s_f-s_i \end{align}$$
Note that the symbol $\Delta$ denotes change, which means “final – initial.”
$\example{1}$ Determine the displacement if $s_1=2$ and $s_2=8$.
$\solution$
In this example, $s_1$ is the initial position and $s_2$ is the final position.
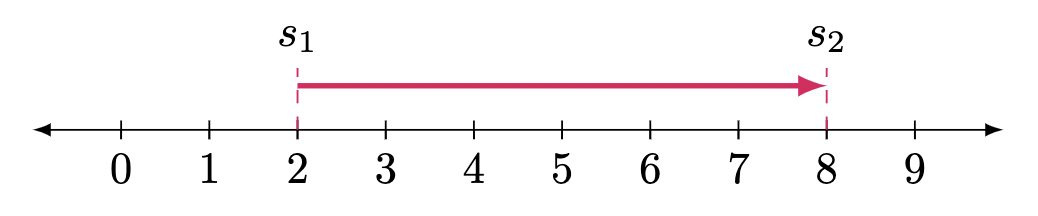
Hence,
\[\begin{align*} \Delta \vv{s} &= s_f-s_i \\ &= s_2-s_1 \\ &= 8-2 \\ &= 5 \text{ units to the $\tcBal{positive}$ direction} \tagans \end{align*}\]$\example{2}$ Determine the displacement if $s_1=5$, $s_2=9$, and $s_3=-2$.
$\solution$
In this example, $s_1$ is the initial position and $s_3$ is the final position.
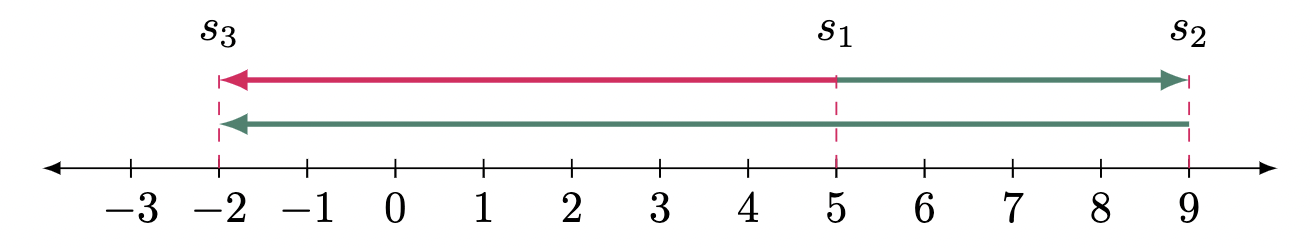
Hence,
\[\begin{align*} \Delta \vv{s} &= s_f-s_i \\ &= s_3-s_1 \\ &= -2-5 \\ &= -7 \text{ units to the $\tcBal{positive}$ direction $\quad$ or} \\ &= 7 \text{ units to the $\tcBal{negative}$ direction} \tagans \end{align*}\]$\example{3}$ A dog runs 100 m to the right then 25 m to the left. Determine its displacement.
$\solution$
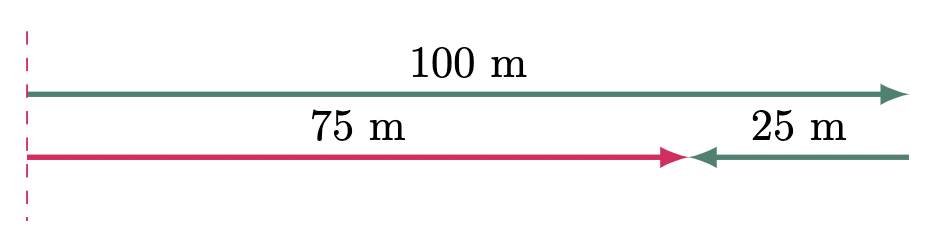
Since the two given displacements are opposite in direction, we can reverse the direction of one displacement to match the other so that we can add the two.
\[\begin{align*} 25 \text{ m to the left} &= -25 \text{ m to the right} \\ \end{align*}\]Hence,
\[\begin{align*} \Delta \vv{s} &= 100\un{m}+(-25\un{m}) \\ &= 75\text{ m to the $\tcBal{right}$} \tagans \end{align*}\]
