Free fall motion is a straightforward example of uniformly accelerated motion. We learned how to solve problems involving uniformed accelerated motion in the previous lesson and apply each kinematic equation to each case. This section will look at how those notions can be applied to objects that experience gravitational acceleration.
Intuitively, we would assume that heavier objects fall faster than lighter objects. However, in the 16$^{\text{th}}$ century, Galileo Galilei, an Italian mathematician, challenged this assumption and projected a different outcome.
Galileo established that all objects fall at the same rate, which may seem counterintuitive given that a piece of paper and a bowling ball does not fall at the same rate when released at the same time and height. However, keep in mind that other external factors can affect its rate, one of which is air resistance, which delays the paper’s fall. Now crumple the paper and perform the same experiment again. The outcome will be quite different. Hence, disregarding all the other external factors, all objects fall at the same rate regardless of their mass.
A free-falling object is an object that is falling under the sole influence of gravitational acceleration. The acceleration due to gravity is denoted by the symbol “$g$,” and in the earth, it is considered to be equal to 9.81 $\mathrm{m/s^2}$ in a downward direction.
Instead of utilizing $a$ as the acceleration in the kinematic equations, in free fall motion, we will be using $g$. Thus,
$$\begin{align} v_f = v_i+gt \label{eq:kinematic eqn gravity 1} \\ \Delta s = \br{ \frac{v_i+v_f}{2} }t \label{eq:kinematic eqn gravity 2} \\ \Delta s = v_it+\frac{1}{2}gt^2 \label{eq:kinematic eqn gravity 3} \\ {v_f}^2 = {v_i}^2+2g\Delta s \label{eq:kinematic eqn gravity 4} \end{align}$$
$\example{1}$ A ball is dropped from the roof of a 90 m tall building. Determine (a) the velocity of the ball when it hits the ground, and (b) the time it took to reach the ground.
$\solution$
$\given$
\(\begin{align*}
v_i &= 0\un{m/s} \text{ (dropped)} & \\
\D{s} &= 90\un{m} \\
g &= 9.81\un{m/s^2}
\end{align*}\)
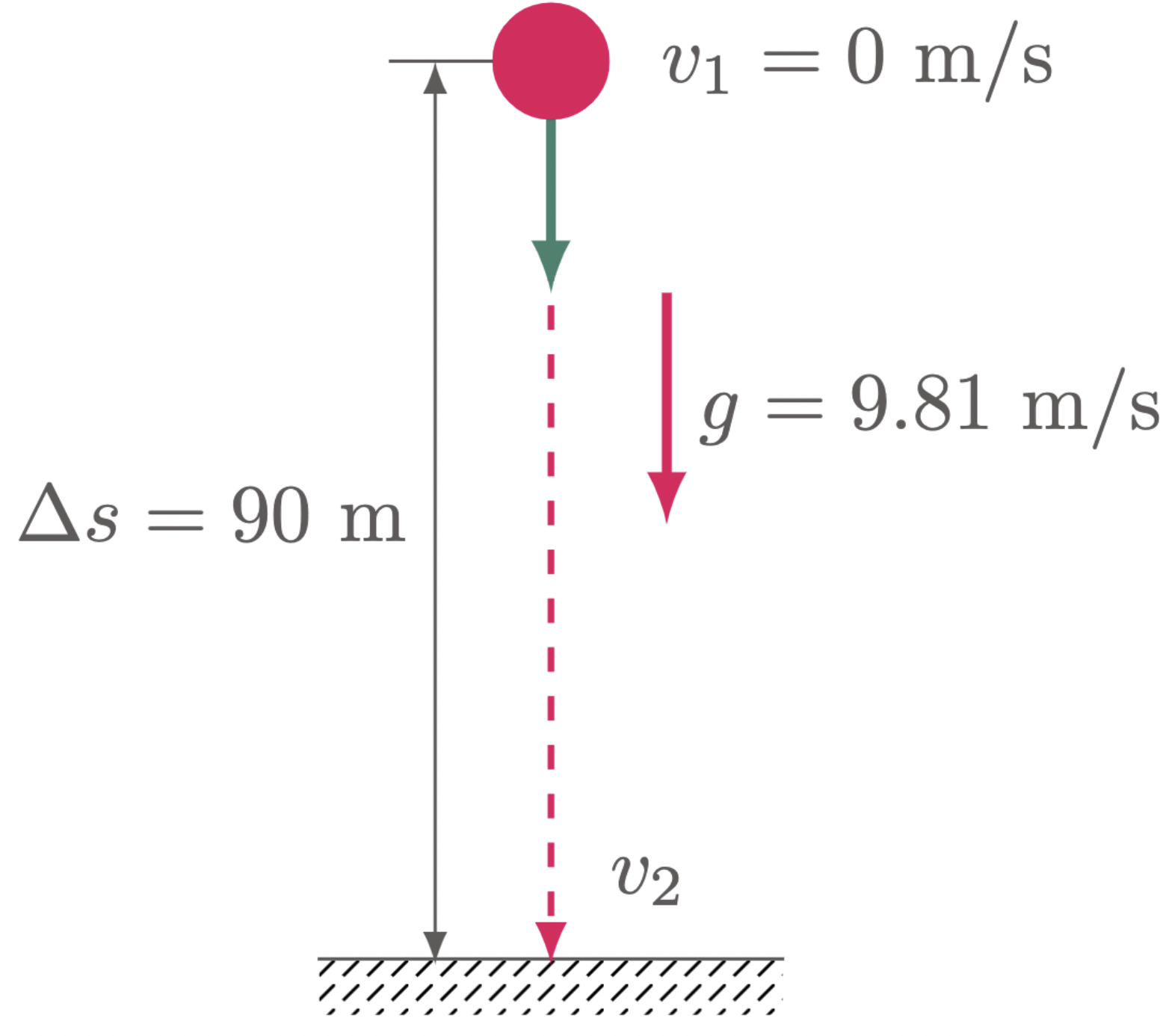
$\For{a}$ $v_f$
The ball is dropped, so the initial velocity is zero $v_1=0$, From the given parameters, the easiest approach is to use $\eref{eq:kinematic eqn gravity 4}$,
\[\begin{align*} {v_2}^2 &= {v_1}^2+2gs \\ {v_2} &= \sqrt{ {v_1}^2+2gs } \\ &= \sqrt{0^2+2(9.81\un{m/s^2})(90\un{m})} \\ &= \sqrt{1765.8 \un{m^2/s^2}} \\ &= 42.02 \un{m/s} \tagans \end{align*}\]$\For{b}$
To solve for the time $t$, use $\eref{eq:kinematic eqn gravity 3}$.
$\example{2}$ An object is thrown upward at a rate of 15 m/s in a perfectly vertical direction. How long does it take to reach the peak of flight?
$\solution$
$\given$
\(\begin{align*}
v_i &= 15\un{m/s} \text{ (upward)} & \\
g &= 9.81\un{m/s^2} \text{ (downward)}
\end{align*}\)
The initial velocity has an upward direction, which is opposite to the direction of the gravitational acceleration. Thus, the object is decelerating ($a=-g$). And note that at the peak of flight, the object has an instantaneous velocity of 0 m/s. From the given parameters, we can simply solve the problem using $\eref{eq:kinematic eqn gravity 1}$,
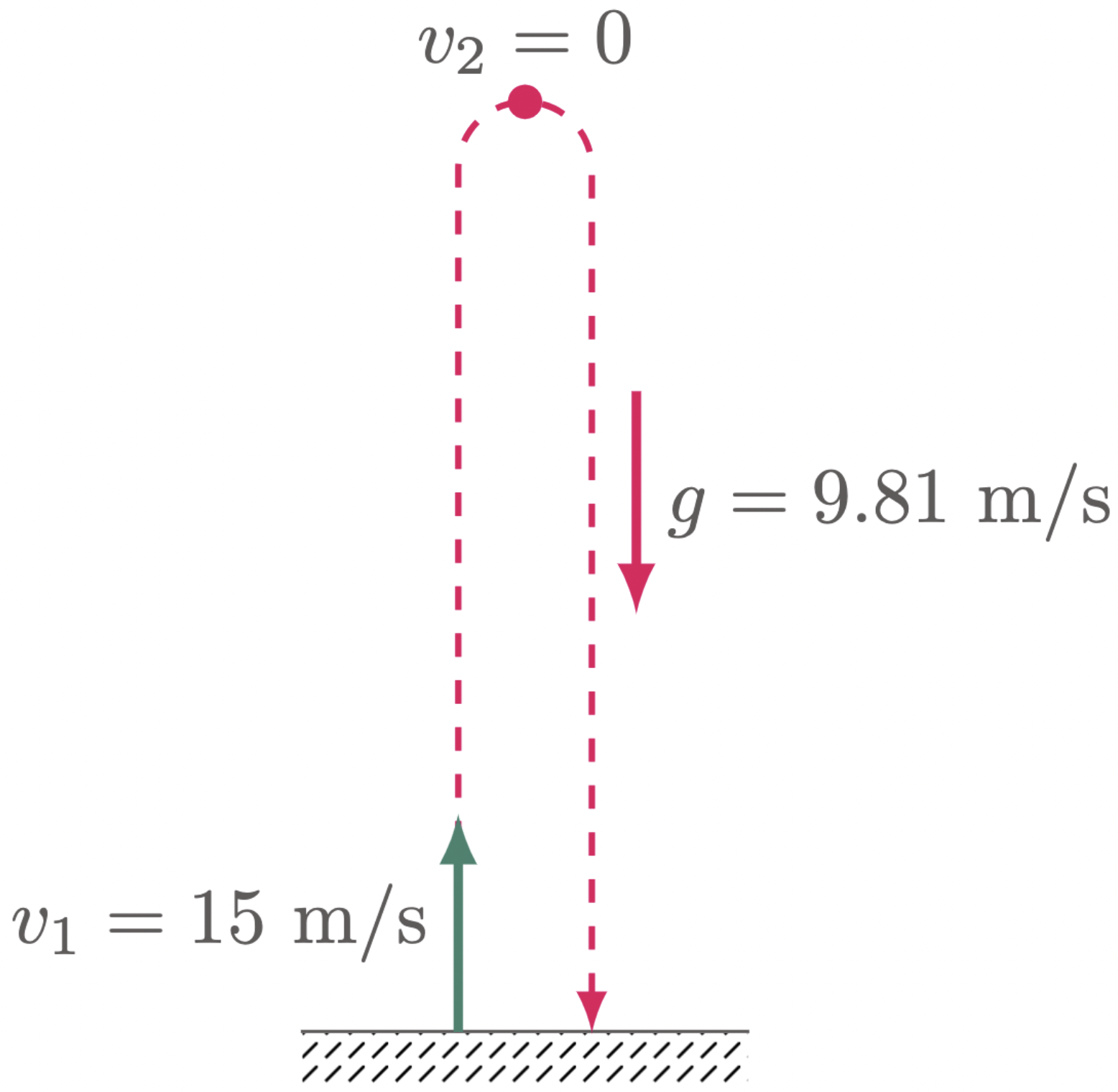
Since the ball is decelerating, $g$ must be negative. Thus,
\[\begin{align*} v_2 &= v_1+(-g)t \\ v_2 &= v_1-gt \\ \end{align*}\]Rearranging the equation gives us,
\[\begin{align*} t &= \frac{v_2-v_1}{-g} \\ &= \frac{0-15\un{m/s}}{-9.81 \un{m/s^2}} \\ &= 1.53 \un{s} \tagans \end{align*}\]
