From the previous lessons, we’ve already learned how to analyze and solve kinematic problems in one dimension. However, in real-world applications, one-dimensional examples are rarely sufficient. To broaden our understanding of motion, we can add another dimension to explore additional applications; these motions are referred to as Two-Dimensional Kinematics. Analyzing motions in two dimensions can be a little overwhelming at first. However, we can simplify the solution by breaking down every parameter into two components so that we can utilize the concepts and equations of one-dimensional kinematics, which we already know how to manipulate.
To understand how displacement, velocity, and acceleration act in a two-dimensional motion, consider a ball thrown at an angle $\theta$ with the horizontal (Figure 1).
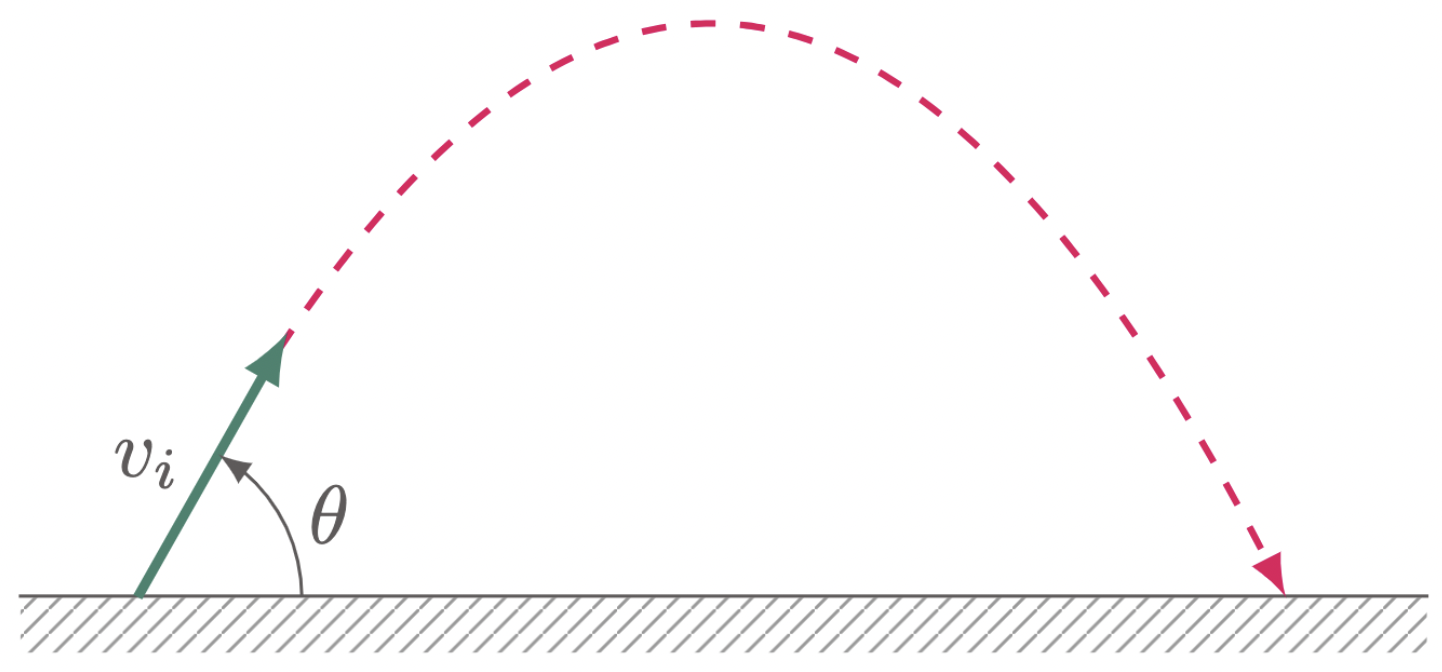
Figure 1: A ball thrown at an angle $\theta$ with the horizontal
Breaking down the motion into two dimensions will result in two independent one-dimensional motions. On the $y$-axis, the ball may seem to be thrown vertically upwards, indicating that it is experiencing a downward acceleration due to gravity. At the $x$-axis, on the other hand, the ball is traveling at a constant rate in a perfectly horizontal motion. Take note that on the $x$-axis, if it is parallel with the horizon, we can disregard acceleration since the gravitational acceleration does not influence it.
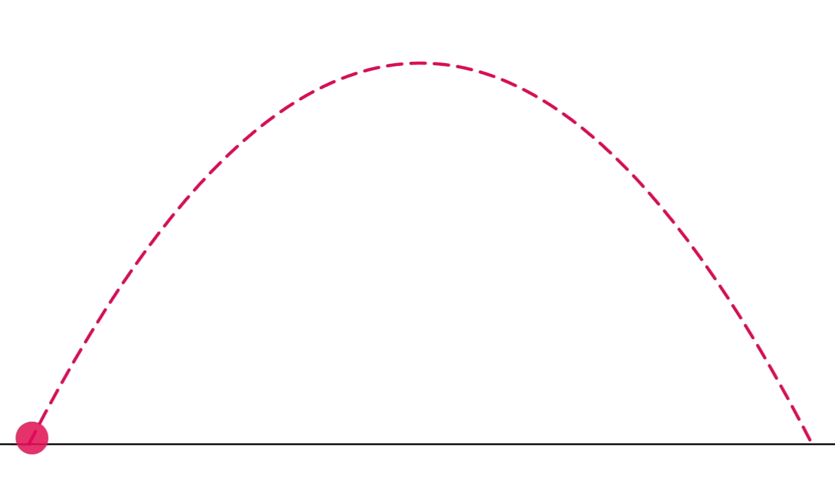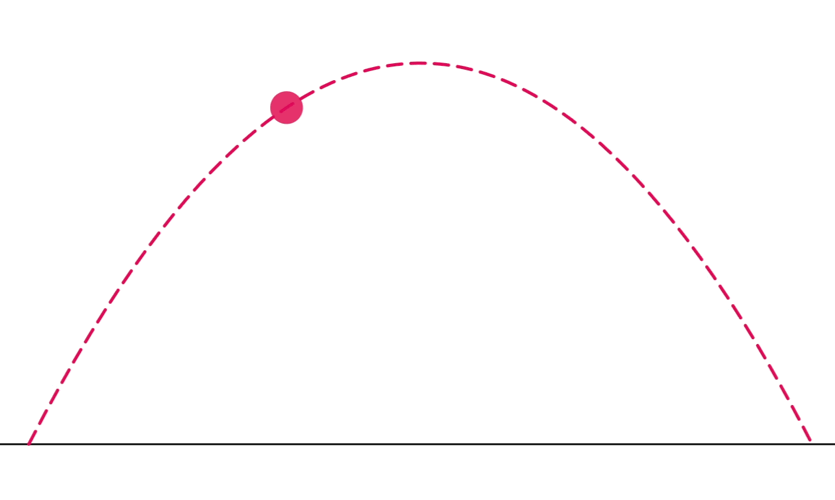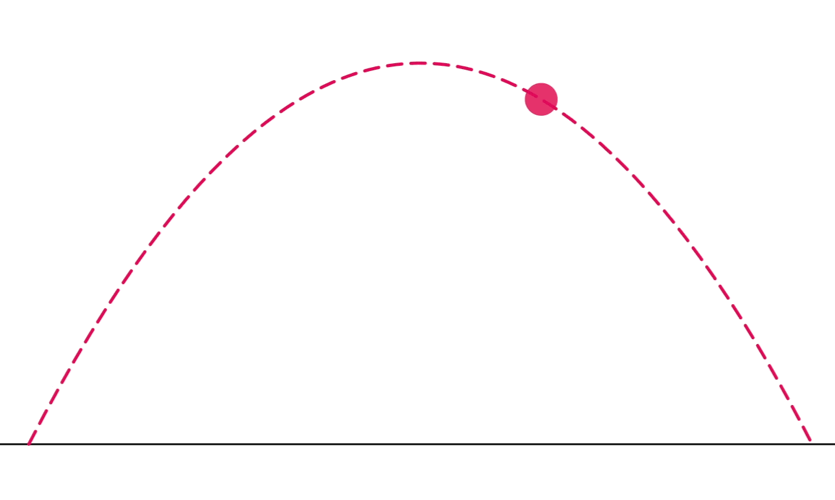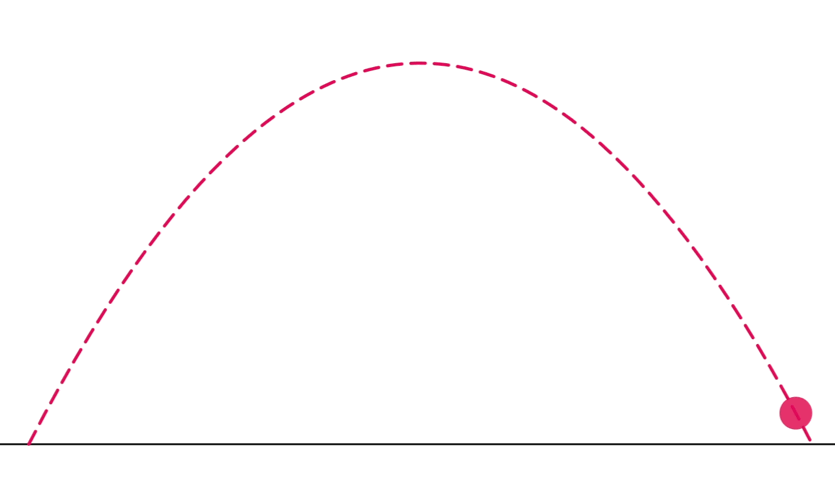
Figure 2: Motion of the ball in two dimensions

Figure 3: Motion of the ball broken down into two components
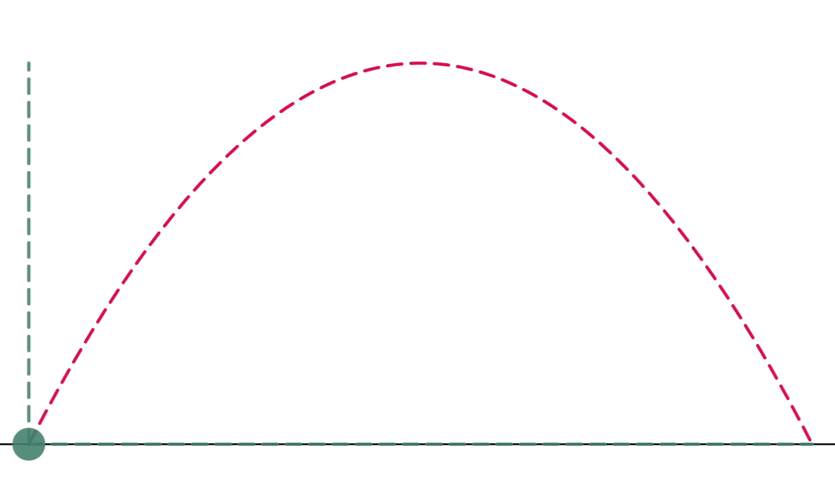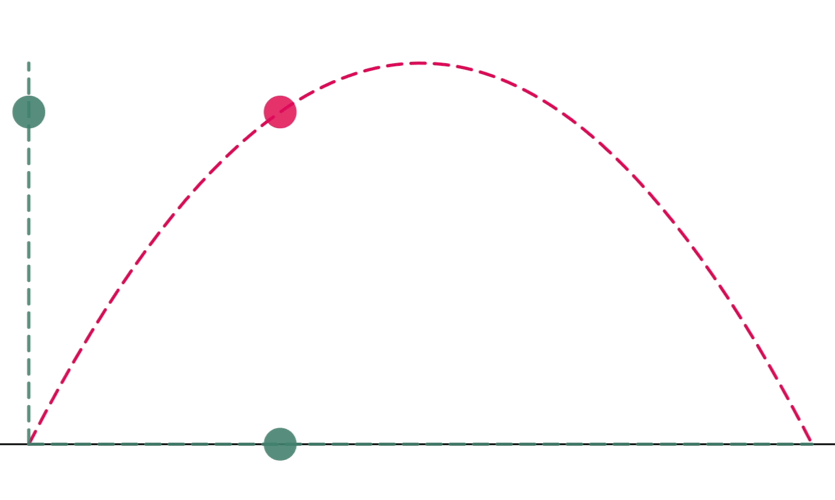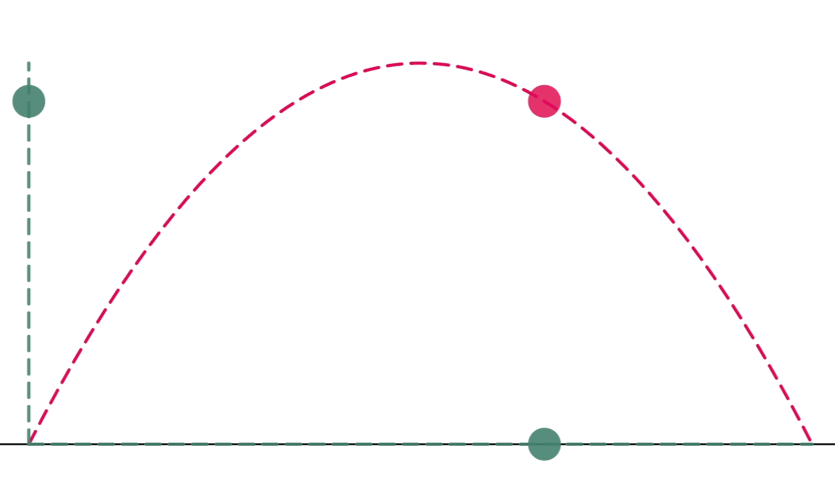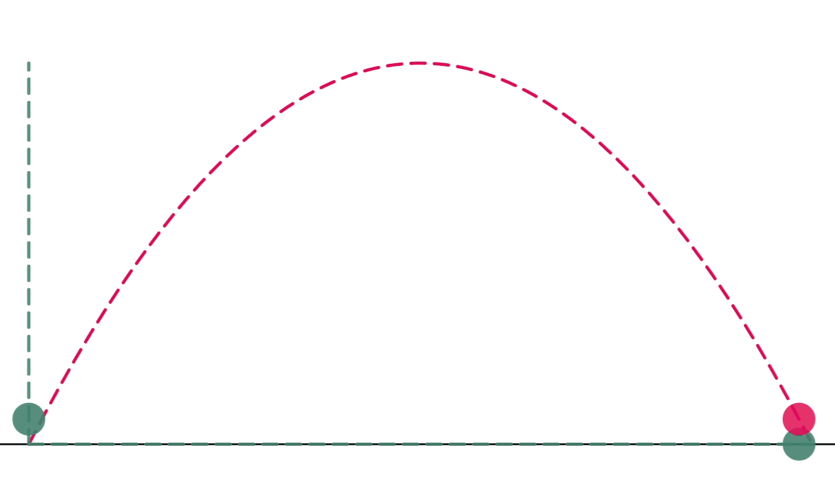
Figure 4: Comparison of the motion of the ball in one and two dimensions
However, in some instances, the $x$-axis will have an acceleration, so breaking down the problem and analyzing what is happening on the object is still necessary.

