Kinematic Equations in Two Dimensions

In two-dimensional kinematics, $x$ and $y$ motions are treated independently so that equations in one-dimensional kinematics can be utilized. But in this section, we will give different variables to each component so that we will not be confused about what motion we are referring to.

$\tcAal{Table 1:}$ Variables in Two-Dimensional Kinematics

\[\begin{array}{ccc} \hline \text{Variable} & \text{$x$-component} & \text{$y$-component} \\ \hline \text{displacement} & x & y \\ \text{initial velocity} & v_{ix} & v_{iy} \\ \text{final velocity} & v_{fx} & v_{fy} \\ \text{acceleration} & a_{x} & a_{y} \\ \text{time elapsed} & t & t \\ \hline \end{array}\]

Substituting the distinct variables into the four kinematic equations, we obtain the following:

$\tcAal{Table 2:}$ Kinematics Equations with Constant Acceleration in Two-Dimensional Motion

\[\begin{array}{cc} \hline \text{$x$-component} & \text{$y$-component} \\ \hline v_{fx} = v_{ix}+a_{x}t & v_{fy} = v_{iy}+a_{y}t \\ x = \br{ \dfrac{v_{ix}+v_{fx}}{2}}t & y = \br{ \dfrac{v_{iy}+v_{fy}}{2} }t \\ x = v_{ix}t+\frac{1}{2}a_{x}t^2 & y = v_{iy}t+\frac{1}{2}a_{y}t^2 \\ {v_{fx}}^2 = {v_{ix}}^2+2a_{x}x & {v_{fy}}^2 = {v_{iy}}^2+2a_{y}y \\ \hline \end{array}\]

As you may have seen, the time $t$ is the same for the $x$ and $y$ motions. Due to the fact that time is a scalar quantity, time will be identical for both components.

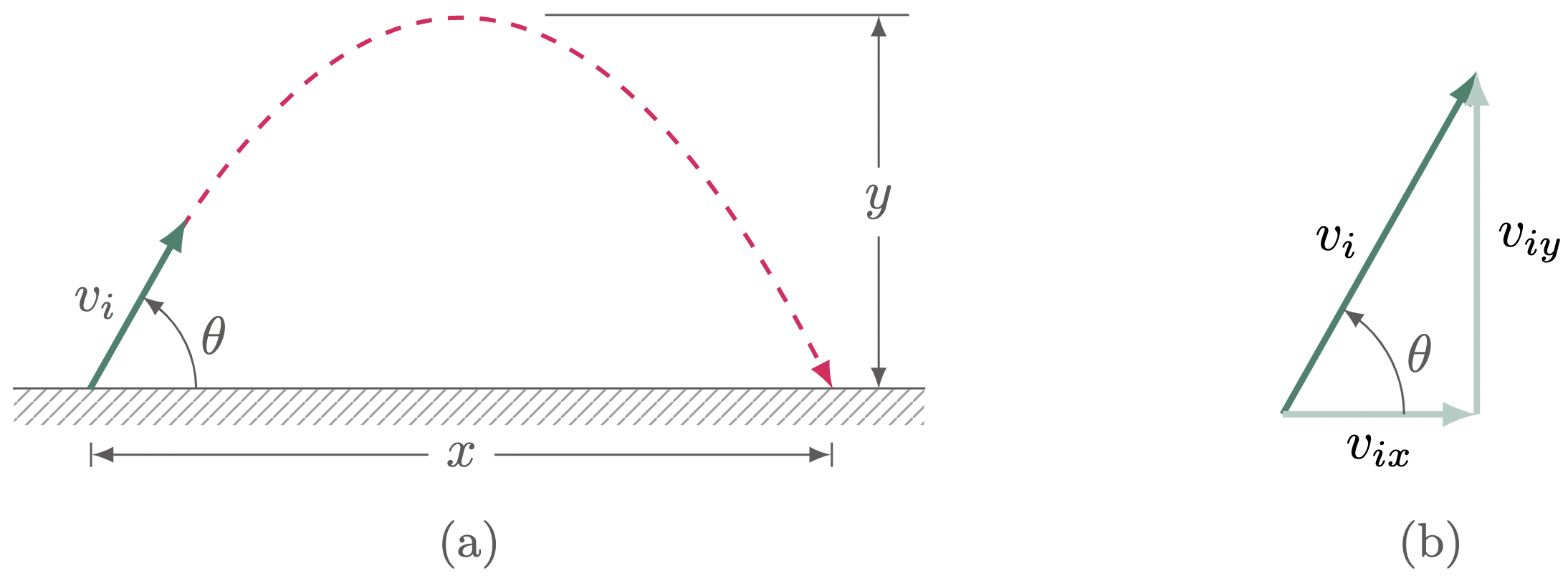
my alt text — *Figure 1: Breaking down a two-dimensional motion into two components*

$\example{1}$ If an object was thrown horizontally at a velocity of 10 m/s from a cliff that has a height of 30 m, determine (a) its initial $x$-component velocity, (b) its initial $y$-component velocity, (c) its final $x$-component velocity, (d) its final $y$-component velocity, (e) its final resultant velocity, (f) its angle at which it strikes the ground, and (g) the distance from the base of the cliff where the projectile lands

$\solution$

$\given$
$v_i=10\un{m/s}$
$y=30\un{m}$

$\required$
(a) $v_{ix}$
(b) $v_{iy}$
(c) $v_{f_x}$
(d) $v_{f_y}$
(e) $v_{f}$
(f) $\theta_f$
(g) $x$

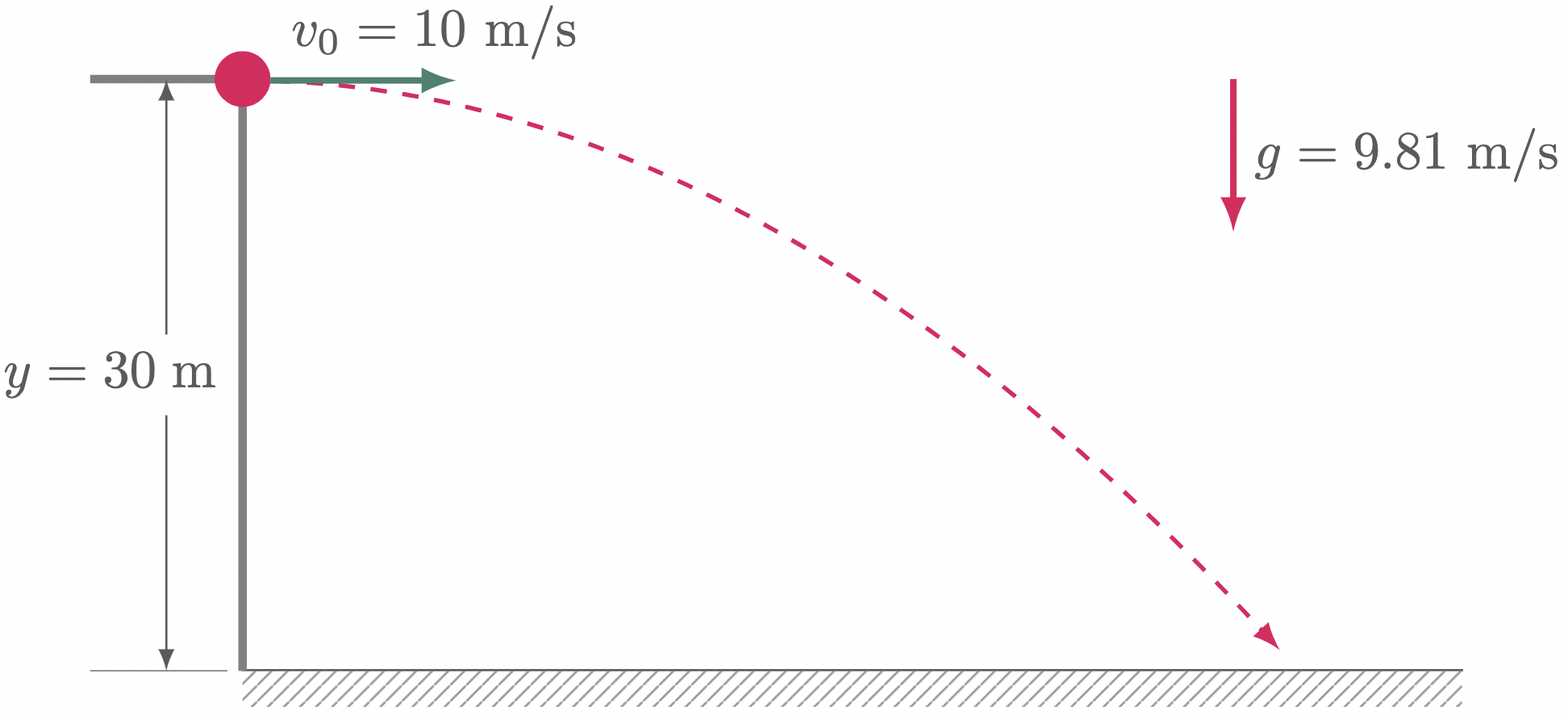
$\For{a}$
The ball was thrown horizontally, so the angle from the horizontal is zero, $\theta=0$.

\[\begin{align*} v_{ix} &= v_{i} \cos\theta \\ &= (10\un{m/s}) \cos(0) \\ &= 10\un{m/s} \tagans \end{align*}\]

$\For{b}$

\[\begin{align*} v_{iy} &= v_{i} \sin\theta \\ &= (10\un{m/s}) \sin(0) \\ &= 0\un{m/s} \tagans \end{align*}\]

$\For{c}$
The motion in the $x$ direction is not influenced by the gravity, so there is no acceleration, thus, the velocity in the $x$ direction is constant.

\[\begin{align*} v_{x} &= v_{ix} = v_{fx} \\ v_{fx} &= 10\un{m/s} \tagans \end{align*}\]

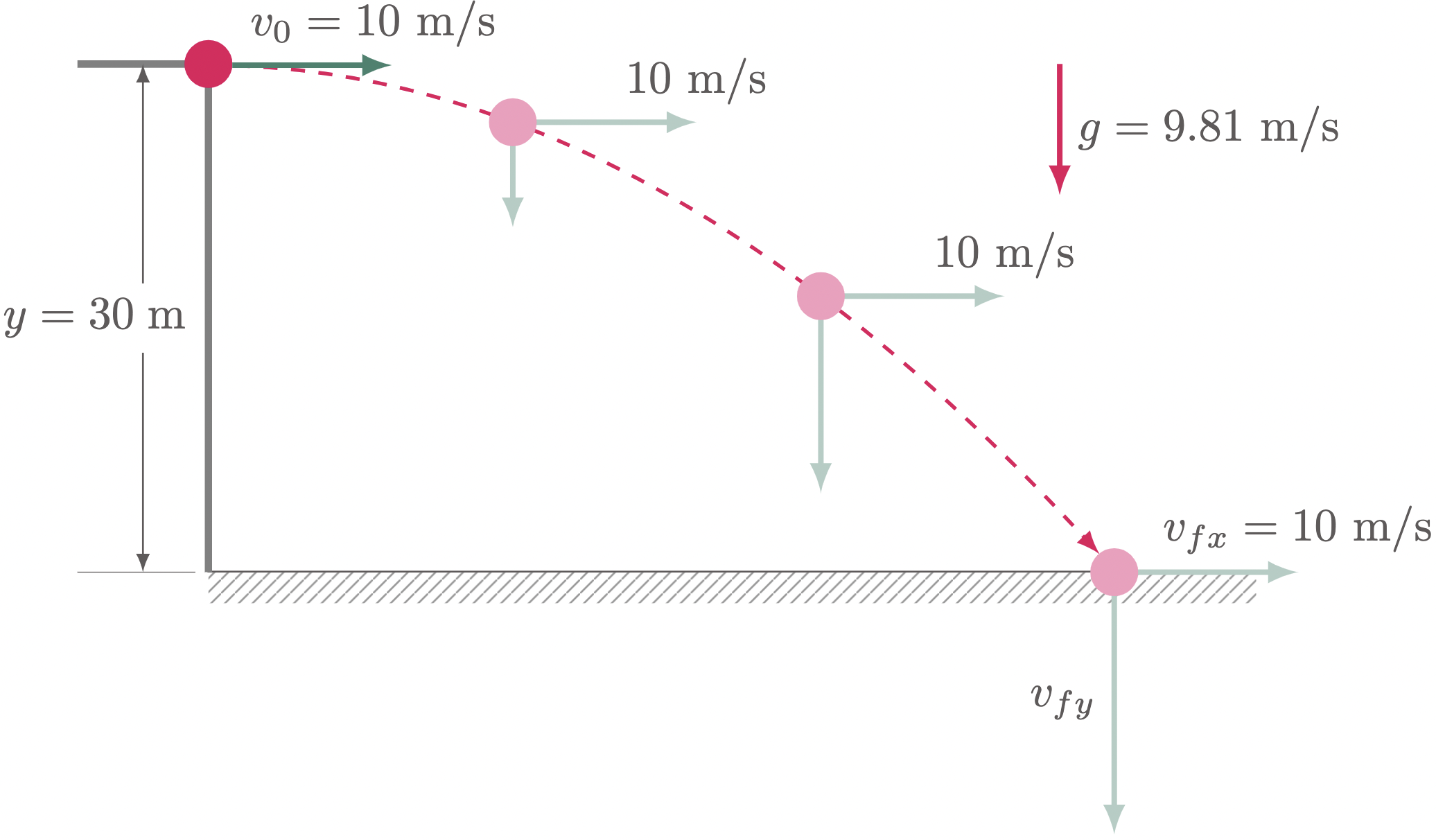
$\For{d}$
The motion in the $y$ direction is influenced by the gravity, so the ball accelerates at a downward direction, $a_y=g=9.81\un{m/s^2}$

\[\begin{align*} {v_{fy}}^2 &= {v_{iy}}^2+2a_{y}y \\ {v_{fy}} &= \sqrt{ {v_{iy}}^2+2gy } \\ &= \sqrt{ 0^2+2(9.81\un{m/s^2})(30\un{m}) } \\ &= 24.26 \un{m/s} \tagans \end{align*}\]

$\For{e}$
The final velocity is the resultant vector of its components, $\vv{v}_f = \vv{v}_{fx}+\vv{v}_{fy}$,

\[\begin{align*} v_f &= \sqrt{ {v_{fx}}^2+{v_{fy}}^2 } \\ &= \sqrt{ (10\un{m/s})^2 + (24.26\un{m/s})^2 } \\ &= 26.24 \un{m/s} \tagans \end{align*}\]

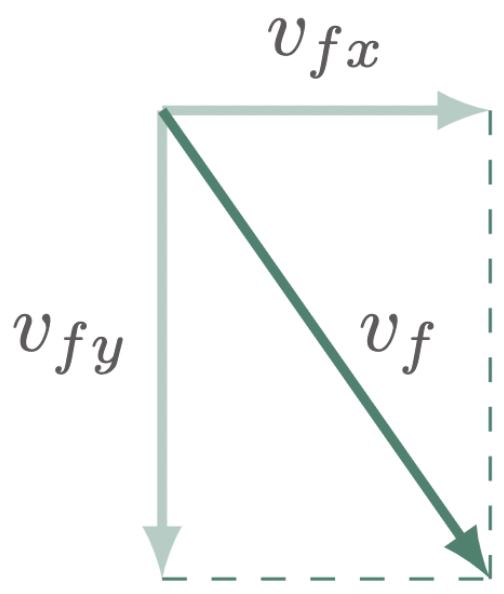
$\For{f}$
Use the tangent function to evaluate the angle at which it strikes the ground,

\[\begin{align*} \tan\theta_f &= \frac{v_{fy}}{v_{fx}} \\ \theta_f &= \tan^{-1} \frac{v_{fy}}{v_{fx}} \\ &= \tan^{-1} \frac{24.26\un{m/s}}{10\un{m/s}} \\ &= 67.60\degg \tagans \end{align*}\]

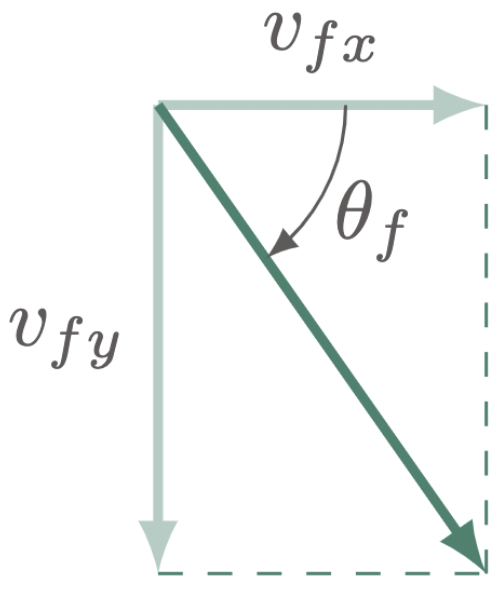
$\For{g}$
There’s no acceleration in the horizontal direction, so we can evaluate the displacement in the $x$-axis using the equation $x=v_xt$. But this equation requires $t$; however, since the time in the $x$ and $y$ directions are just the same, we can first find $t$ from the vertical direction,

\[\begin{align*} y &= v_{iy}t + \frac{1}{2} gt^2 \\ 30\un{m} &= (0\un{m/s})t + \frac{1}{2} (9.81\un{m/s^2})t^2 \\ t &= \sqrt{ \frac{2(30\un{m})}{9.81\un{m/s^2}} } \\ &= 2.473 \un{s} \end{align*}\]

Then substituting the time to the equation gives us,

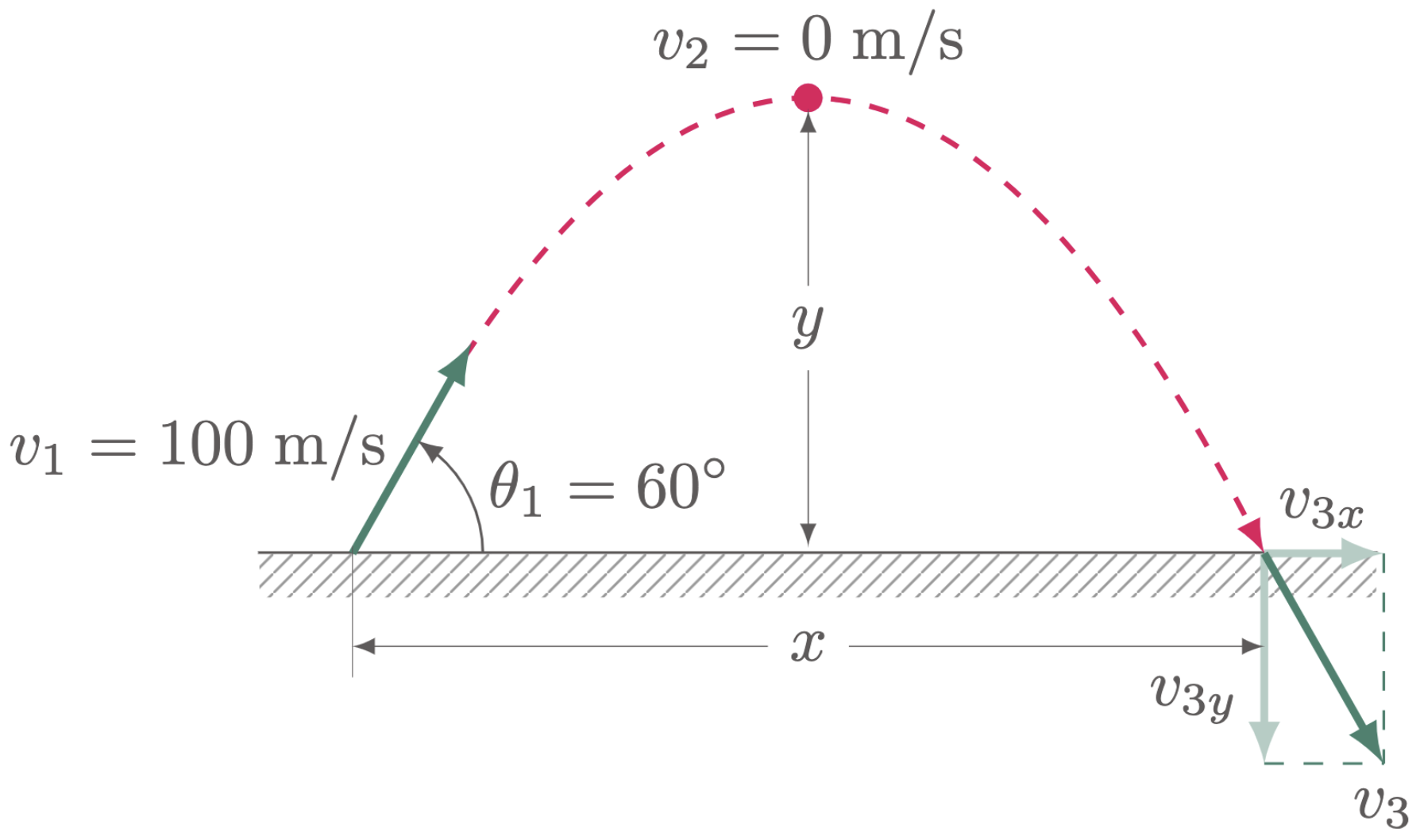
\[\begin{align*} x &= v_xt \\ &= (10\un{m/s})(2.473\un{s}) \\ &= 24.73\un{m} \tagans \end{align*}\]

$\example{2}$ A projectile was launched at a velocity of 100 m/s at a 60 degree angle and fell at the same level it was launched. Determine (a) its initial $x$-component velocity, (b) its initial $y$-component velocity, (c) the time to reach its maximum height, (d) the maximum height reached, (e) the time of flight, (f) its final $x$-component velocity, (g) its final $y$-component velocity, (h) its final resultant velocity, (i) its angle at which it strikes the ground, and (j) the range of the projectile.

$\solution$

$\given$
$v_1=100\un{m/s}$
$\theta_1=30\degg$

$\required$
(a) $v_{1x}$
(b) $v_{1y}$
(c) $t_{1-2}$
(d) $y$
(e) $t_{1-3}$
(f) $v_{3x}$
(g) $v_{3y}$
(h) $v_{3}$
(i) $\theta_3$
(j) $x$

$\For{a}$

\[\begin{align*} v_{1x} &= v_{1} \cos\theta_1 \\ &= (100\un{m/s}) \cos(60\degg) \\ &= 50\un{m/s} \tagans \end{align*}\]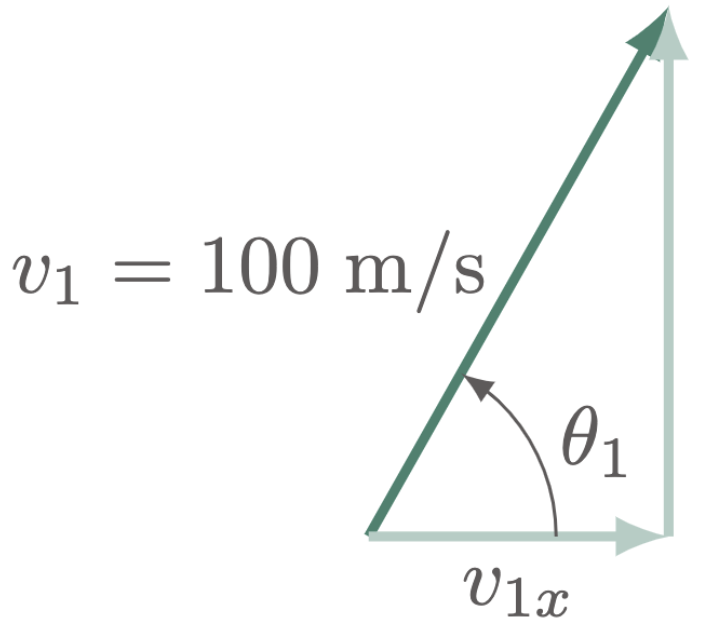

$\For{b}$

\[\begin{align*} v_{1y} &= v_{1} \sin\theta_1 \\ &= (100\un{m/s}) \sin(60\degg) \\ &= 86.60\un{m/s} \tagans \end{align*}\]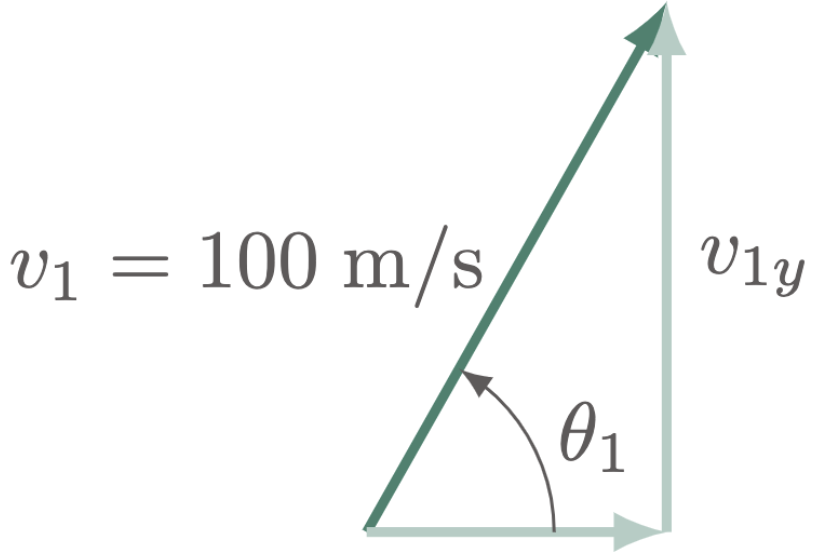

$\For{c}$
Consider the projectile moving from point 1 to point 2, the motion of the projectile is going upward, but the gravitational acceleration is in a downward direction. Hence, the ball is decelerating,

\[\begin{align*} {v_{2y}} &= {v_{1y}}+(-g)t_{1-2} \\ {v_{2y}} &= {v_{1y}}-gt_{1-2} \\ t_{1-2} &= \frac{v_{1y}-v_{2y}}{g} \\ &= \frac{86.60\un{m/s}-0\un{m/s}}{9.81\un{m/s^2}} \\ &= 8.83\un{s} \tagans \end{align*}\]

$\For{d}$
The maximum height reached by the projectile before it stopped rising is the vertical displacement $y$,

\[\begin{align*} y &= \br{ \frac{v_{1y}+v_{2y}}{2} } t_{1-2} \\ &= \br{ \frac{86.60\un{m/s}+0\un{m/s}}{2} } (8.83\un{s}) \\ &= 382.34\un{m} \tagans \end{align*}\]

$\For{e}$
The time of flight is the time for the whole duration of the projectile suspended in the air from the point it was launched till it was dropped. Since we’ve already solved the time from point 1 to point 2, what’s left to find is for the second half of its flight, which is when the time the projectile is falling $t_{2-3}$.

\[\begin{align*} y &= v_{2y}t_{2-3}+\frac{1}{2}g(t_{2-3})^2 \\ 382.34\un{m} &= (0\un{m/s})t_{2-3} + \frac{1}{2}(9.81\un{m/s^2})(t_{2-3})^2 \\ t_{2-3} &= \sqrt{ \frac{2(382.34\un{m})}{9.81\un{m/s^2}} } \\ &= 8.83\un{s} \end{align*}\]

Hence, the total time is,

\[\begin{align*} t_{1-3} &= t_{1-2}+t_{2-3} \\ &= 8.83\un{s} + 8.83\un{s} \\ &= 17.66 \un{s} \tagans \end{align*}\]

$\For{f}$
The motion in the $x$ direction is not influenced by the gravity, so there is no acceleration, thus, the velocity in the $x$ direction is constant.

\[\begin{align*} v_{x} &= v_{1x} = v_{2x} = v_{3x} \\ v_{3x} &= 50\un{m/s} \tagans \end{align*}\]

$\For{g}$
The projectile from point 2 to point 3 is moving downwards, so the projectile is accelerating,

\[\begin{align*} v_{3y} &= v_{2y}+g(t_{2-3}) \\ &= 0\un{m/s}+(9.81\un{m/s^2})(8.83\un{s}) \\ &= 86.60\un{m/s} \tagans \end{align*}\]

$\For{h}$

\[\begin{align*} v_3 &= \sqrt{ {v_{3x}}^2+{v_{3y}}^2 } \\ &= \sqrt{ (50\un{m/s})^2+(86.60\un{m/s})^2 } \\ &= 100\un{m/s} \tagans \end{align*}\]

$\For{i}$
Use the tangent function to evaluate the angle at which it strikes the ground,

\[\begin{align*} \tan\theta_3 &= \frac{v_{3y}}{v_{3x}} \\ \theta_3 &= \tan^{-1} \frac{v_{3y}}{v_{3x}} \\ &= \tan^{-1} \frac{86.61\un{m/s}}{50\un{m/s}} \\ &= 60\degg \tagans \end{align*}\]

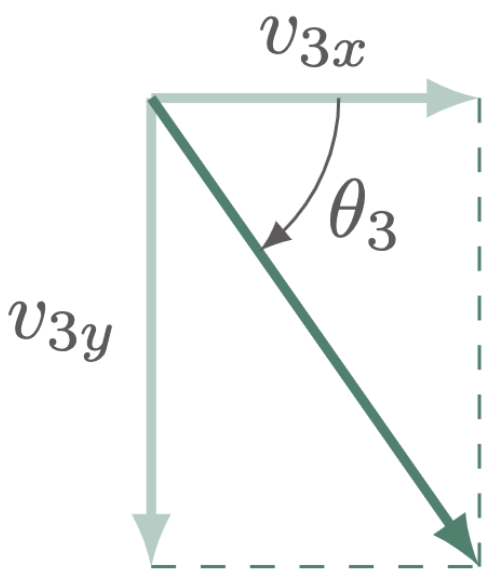
$\For{j}$
The range of the projectile is the horizontal distance from its starting point to the end point. And since there is no acceleration in the $x$ direction,

\[\begin{align*} x &= v_x(t_{1-3}) \\ &= 50\un{m/s}(17.66\un{s}) \\ &= 883\un{m} \tagans \end{align*}\]

Kinematic Equations in Two Dimensions

© 2022 Lemniscate Institute