A well-known application of the rate of change is when it involves motion. Moreover, in physics, velocity is a fundamental concept that must be learned at the start of the course.
To understand the difference between Average and Instantaneous Velocity, consider Figure 1, which represents a position vs. time graph, where the vertical axis represents the object’s position $s$ and the horizontal axis (independent variable) represents the time $t$.
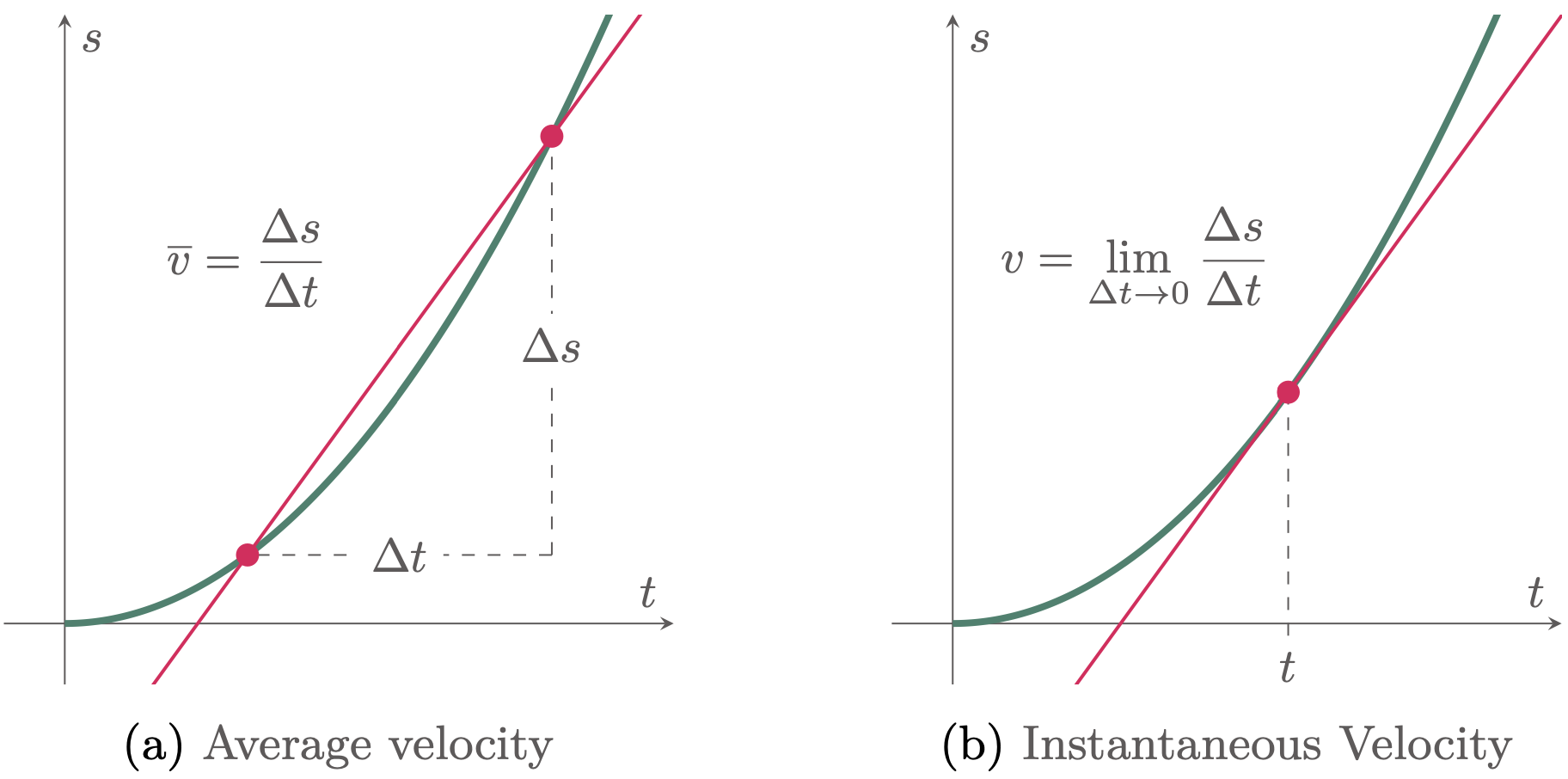
Figure 1: Graphical representation of average and instantaneous velocities
Average velocity is defined as the change of the displacement $\D{s}$ of an object divided by the time interval $\D{t}$. Graphically, the average velocity can be expressed as the slope of the secant line connecting the two positions (Figure 1a).
$$\begin{align} \overline{v}=\frac{\Delta s}{\Delta t} \end{align}$$
Instantaneous velocity, on the other hand, is the velocity of the object at a specific instant. To understand this, let us have a simple example.
Suppose a stray dog chased a student, his initial instinct tells him to run as fast as possible, say he is running at a rate of 10 m/s, but as time passed by, he starts slowing down to a rate of 4 m/s, then somehow realized that the dog already stopped chasing him, so he then stopped running.
Instantaneous velocity, is the velocity at a certain instant, so at the time he hit his velocity at 10 m/s that was his instantaneous velocity at that certain moment. And at the time he stopped, he has an instantaneous velocity of 0 m/s. Hence, instantaneous velocity is denoted as,
$$\begin{align} v = \frac{ds}{dt} = \lim_{\Delta t \to 0} \frac{\Delta{s}}{\Delta{t}} \end{align}$$
Instantaneous velocity can be represented as the derivative of the function at a specific point. Graphically, the instantaneous velocity is the slope of the tangent line at a particular time (Figure 1b).
$\example{1}$ What is the instantaneous velocity of a car at $t= 5$ sec if its displacement is defined by the equation: $s=2t^2+3t-5$ meters.
$\solution$
From the given equation, the displacement is a function of its time. To determine the instantaneous velocity of the car at a specific instant, differentiate the function with respect to time,
\[\begin{align*} s+\D{s} &= 2(t+\D{t})^2+3(t+\D{t})-5 \\ \D{s} &= \cancel{2t^2}+4t\D{t}+2\D{t}^2+\cancel{3t}+3\D{t}-\cancel{5} - (\cancel{2t^2}+\cancel{3t}-\cancel{5}) \\ &= 4t\D{t}+2\D{t}^2+3\D{t} \\ \frac{\D s}{\D t} &= \frac{\cancel{\D t}(4t+2\D{t}+3)}{\cancel{\D t}} \\ \frac{ds}{dt} &= \lim_{\D t\to 0} (4t+2\D{t}+3) \\ &= 4t+3 \end{align*}\]At $t=5\un{sec}$,
\[\begin{align*} &= 4(5)+3 \\ &= 23 \un{m/s} \tagans \end{align*}\]$\example{2}$ A ball is thrown vertically upward with the displacement from its initial point defined by the equation: $s=160t-16t^2$ ft, what is the height of the ball in ft. at the moment it stopped rising?
$\solution$
When a ball is thrown upward, it will eventually stop rising at its peak. And the instantaneous velocity of the ball when it reaches its peak is zero.
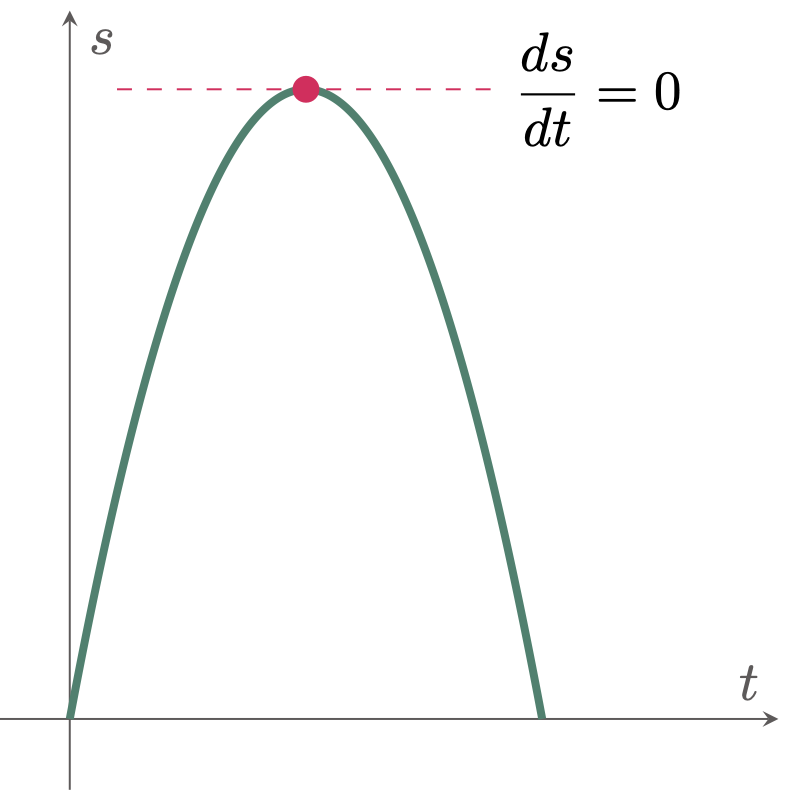
Differentiate $s$ with respect to $t$,
\[\begin{align*} s+\D{s} &= 160(t+\D t)-16(t+\D t)^2 \\ \D{s} &= \cancel{160t}+160\D t-\cancel{16t^2}-32t\D{t}-16\D{t}^2 - (\cancel{160t}-\cancel{16t^2}) \\ &= 160\D{t}-32t\D{t}-16\D{t}^2 \\ \frac{\D s}{\D t} &= \frac{\cancel{\D t} (160-32t-16\D{t})}{\cancel{\D t}} \\ \frac{ds}{dt} &= \lim_{\D t\to 0} (160-32t-16\D{t}) \\ &= 160-32t \end{align*}\]At the peak of flight of the ball, $\frac{ds}{dt}=0$,
\[\begin{align*} 0 &= 160-32t \\ t &= \frac{160}{32} \\ &= 5 \end{align*}\]Thus, it takes 5 sec for the ball to reach the peak. So, substitute $t=5$ to the function,
\[\begin{align*} s &= 160(5)-16(5)^2 \\ &= 400\un{ft} \tagans \end{align*}\]Hence, the ball will stop rising after it reaches the height of 400 ft.

